第八集：魔法阵 NTT求循环卷积
题目来源：http://www.fjutacm.com/Problem.jsp?pid=3283
题意：给两串长度为n的数组a和b，视为环，a和b可以在任意位置开始互相匹配得到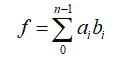
这个函数的值，求这个函数的值最大是多少；
很明显是FFT，但是数据范围是n是1e5，a[i]和b[i]是1e6；精度会丢很多，也就是要NTT解决，那么要选一个不会影响答案的P，因为最大值为1e5*1e6*1e6；那么我们选一个1e17以上的就差不多了，然后就是求循环卷积的步骤，对此，我建议你们算一下这个，[a1、a2、a3、a1、a2、a3]*[b1、b2、b3]，列出全部结果(乘法一样的操作，注意每一位乘法的偏移位置)，你会发现得到的新集合去掉头上n-1个以及尾部n-1个就可以得到全部的线性卷积组合，那么我们就可以求那个两个数组的卷积得到的数组里直接找最大：
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 #include<algorithm> 5 using namespace std; 6 typedef long long ll; 7 const ll PMOD=(27ll<<56)+1, PR=5; 8 const int N=1e6+7; 9 static ll qp[30]; 10 ll res[N]; 11 inline ll Mul(ll a,ll b){ 12 if(a>=PMOD)a%=PMOD; 13 if(b>=PMOD)b%=PMOD; 14 return (a*b-(ll)(a/(long double)PMOD*b+1e-8)*PMOD+PMOD)%PMOD; 15 } 16 struct NTT__container{ 17 NTT__container( ){ 18 int t,i; 19 for( i=0; i<21; i++){///注意循环上界与2n次幂上界相同 20 t=1<<i; 21 qp[i]=quick_pow(PR,(PMOD-1)/t); 22 } 23 } 24 ll quick_pow(ll x,ll n){ 25 ll ans=1; 26 while(n){ 27 if(n&1) 28 ans=Mul(ans,x); 29 x=Mul(x,x); 30 n>>=1; 31 } 32 return ans; 33 } 34 int get_len(int n){///计算刚好比n大的2的N次幂 35 int i,len; 36 for(i=(1<<30); i; i>>=1){ 37 if(n&i){ 38 len=(i<<1); 39 break; 40 } 41 } 42 return len; 43 } 44 inline void NTT(ll F[],int len,int type){ 45 int id=0,h,j,k,t,i; 46 ll E,u,v; 47 for(i=0,t=0; i<len; i++){///逆位置换 48 if(i>t) swap(F[i],F[t]); 49 for(j=(len>>1); (t^=j)<j; j>>=1); 50 } 51 for( h=2; h<=len; h<<=1){///层数 52 id++; 53 for( j=0; j<len; j+=h){///遍历这层上的结点 54 E=1;///旋转因子 55 for(int k=j; k<j+h/2; k++){///遍历结点上的前半序列 56 u=F[k];///A[0] 57 v=Mul(E,F[k+h/2]);///w*A[1] 58 ///对偶计算 59 F[k]=(u+v)%PMOD; 60 F[k+h/2]=((u-v)%PMOD+PMOD)%PMOD; 61 ///迭代旋转因子 62 E=Mul(E,qp[id]);///qp[id]是2^i等分因子 63 } 64 } 65 } 66 if(type==-1){ 67 int i; 68 ll inv; 69 for(i=1; i<len/2; i++)///转置，因为逆变换时大家互乘了对立点的因子 70 swap(F[i],F[len-i]); 71 inv=quick_pow(len,PMOD-2);///乘逆元还原 72 for( i=0; i<len; i++) 73 F[i]=Mul(F[i],inv); 74 } 75 } 76 void mul(ll x[],ll y[],int len){///答案存在x中 77 int i; 78 NTT(x,len,1);///先变换到点值式 79 NTT(y,len,1);///先变换到点值式上 80 for(i=0; i<len; i++) 81 x[i]=Mul(x[i],y[i]);///在点值上点积 82 NTT(x,len,-1);///再逆变换回系数式 83 } 84 } cal; 85 ll a[N], b[N]; 86 int main() { 87 int n; 88 scanf("%d",&n); 89 for(int i=0;i<n;i++) 90 scanf("%lld",a+i), a[i+n]=a[i]; 91 for(int i=0;i<n;i++) 92 scanf("%lld",&b[n-1-i]); 93 int len=cal.get_len(n+n+n); 94 cal.mul(a, b, len); 95 ll mx=0; 96 for(int i=0;i<len;i++){///完整的组合肯定更大所以说直接找最大 97 if(mx<a[i]){ 98 mx=a[i]; 99 } 100 } 101 printf("%lld\n",mx); 102 return 0; 103 }
还有优化的解法，这我真不知道为什么，可能是因为前后相加刚好可以组合出全部组合：
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 #include<algorithm> 5 using namespace std; 6 typedef long long ll; 7 const ll PMOD=(27ll<<56)+1, PR=5; 8 const int N=1e6+7; 9 static ll qp[30]; 10 ll res[N]; 11 inline ll Mul(ll a,ll b){ 12 if(a>=PMOD)a%=PMOD; 13 if(b>=PMOD)b%=PMOD; 14 //if(n<=1000000000)return a*b%n; 15 return (a*b-(ll)(a/(long double)PMOD*b+1e-8)*PMOD+PMOD)%PMOD; 16 } 17 struct NTT__container{ 18 NTT__container( ){ 19 int t,i; 20 for(i=0; i<21; i++){///注意循环上界与2n次幂上界相同 21 t=1<<i; 22 qp[i]=quick_pow(PR,(PMOD-1)/t); 23 } 24 } 25 ll quick_pow(ll x,ll n){ 26 ll ans=1; 27 while(n){ 28 if(n&1) 29 ans=Mul(ans,x); 30 x=Mul(x,x); 31 n>>=1; 32 } 33 return ans; 34 } 35 int get_len(const int &n){///计算刚好比n大的2的N次幂 36 int i, len; 37 for(i=(1<<30); i; i>>=1){ 38 if(n&i){ 39 len=(i<<1);break; 40 } 41 } 42 return len; 43 } 44 inline void NTT(ll F[], const int &len, int type){ 45 int id=0, h, j, t, i; 46 ll E,u,v; 47 for(i=0,t=0; i<len; i++){///逆位置换 48 if(i>t) swap(F[i],F[t]); 49 for(j=(len>>1); (t^=j)<j; j>>=1); 50 } 51 for( h=2; h<=len; h<<=1){///层数 52 id++; 53 for( j=0; j<len; j+=h){///遍历这层上的结点 54 E=1;///旋转因子 55 for(int k=j; k<j+h/2; k++){///遍历结点上的前半序列 56 u=F[k];///A[0] 57 v=Mul(E,F[k+h/2]);///w*A[1] 58 ///对偶计算 59 F[k]=(u+v)%PMOD; 60 F[k+h/2]=((u-v)%PMOD+PMOD)%PMOD; 61 ///迭代旋转因子 62 E=Mul(E,qp[id]);///qp[id]是2^i等分因子 63 } 64 } 65 } 66 if(type==-1){ 67 int i; 68 ll inv; 69 for(i=1; i<len/2; i++)///转置，因为逆变换时大家互乘了对立点的因子 70 swap(F[i],F[len-i]); 71 inv=quick_pow(len,PMOD-2);///乘逆元还原 72 for( i=0; i<len; i++) 73 F[i]=Mul(F[i],inv); 74 } 75 } 76 void mul(ll x[],ll y[],int len){///答案存在x中 77 int i; 78 NTT(x,len,1);///先变换到点值式 79 NTT(y,len,1);///先变换到点值式上 80 for(i=0; i<len; i++) 81 x[i]=Mul(x[i],y[i]);///在点值上点积 82 NTT(x,len,-1);///再逆变换回系数式 83 } 84 } cal; 85 ll a[N], b[N]; 86 int main() { 87 int n; 88 scanf("%d",&n); 89 for(int i=0;i<n;i++) 90 scanf("%lld",a+i); 91 for(int i=0;i<n;i++) 92 scanf("%lld",&b[n-1-i]); 93 int len=cal.get_len(n+n); 94 cal.mul(a, b, len); 95 ll mx=0; 96 for(int i=0;i<len;i++){ 97 a[i]+=a[i+n]; 98 if(mx<a[i]){ 99 mx=a[i]; 100 } 101 } 102 printf("%lld\n",mx); 103 return 0; 104 }
