主席树学习笔记

 

　　主席树又名可持久化线段树，即可以保存线段树的历史版本，比如得到第k次操作后的值这样的命令。

　　我们看一颗线段树：

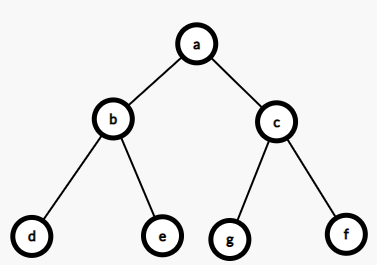
　　对于这颗线段树我们进行q次单点修改，要你求第k次的线段树是什么样的，那么很明显，我们最简单的是建立q颗线段树，假设该线段树有n个节点，我们一般开线段树大小是n*4，那么总空间利用就是q*n*4，很明显不行，那么我们再观察一下，其实每次修改的时候只有一条链被改变了，也就是这条链就是第i次修改所改变的东西，那么我们一个个记录链，这样的话每条链长度为logn，空间复杂度就是q*logn，比刚才好了不知道多少！然后对于每条链要记录他的子节点(有的话)，以及和他相连的点里没改变的，比如下面这个图(假设改变e点)：

　　e`，b`，a`就是改变的的值，然后你按照以a`为根开始往下跑相连的点，此时记录的也确实是第1次修改以后的树，也就是说对没修改的点实行共用策略，这就是一颗对前缀建立的树！！！！下面看代码：

　　这题是：http://www.fjutacm.com/Problem.jsp?pid=2439

　　转    自：http://acm.hdu.edu.cn/showproblem.php?pid=2665

#include<vector>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define mid ((l+r)/2)
#define C(A, B) memset(A, B, sizeof(A))
using namespace std;
const int N=100007;
const int INF=0x3f3f3f3f;
int n, m, a[N], x, y, k;
vector<int> E;
void read(int &x){
    int f=1;x=0;char s=getchar();
    while((s<'0')|(s>'9')){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}
int getid(int x){ return lower_bound(E.begin(), E.end(), x)-E.begin()+1; }
struct No{int l, r, sum;} T[N*40];      　　　///一般对于一颗线段树开2qlogn的数组大小
int cnt, root[N];
void update(int l, int r, int &x, int y, int pos){
    T[++cnt]=T[y];                           ///将上一个对应节点的值记录下来，包括上一个对应节点的左右子节点
    T[cnt].sum++;                            ///在这里对变化的值直接加
    x=cnt;                                   ///x是引用，及root[i]=x=cnt记录这棵树的根节点的位置，其他也一样的是记录子节点的位置
    if(l==r){                                ///不需要解释吧！！需要的自己线段树巩固好
        return ;
    }
    if(mid>=pos){                            ///同线段树判断，还有，这个节点的更新完全仰赖于上一棵树对应节点的值，也就是这两棵树要同左同右，所以说左右区间移动的时候才是这样的，然后无限递归得到这颗树
        update(l, mid, T[x].l, T[y].l, pos);
    }else{
        update(mid+1, r, T[x].r, T[y].r, pos);
    }
}
int query(int l, int r, int x, int y, int k){
    if(l==r){
        return l;
    }
    int sum=T[T[y].l].sum-T[T[x].l].sum;    ///得到y-x+1区间线段树的真正的和
    if(sum>=k){                             ///同左同右
        return query(l, mid, T[x].l, T[y].l, k);
    }else{
        return query(mid+1, r, T[x].r, T[y].r, k-sum);
    }
}
int main( ){
    int T;
    scanf("%d", &T);
    while(T--){
        cnt=0; E.clear();
        read(n), read(m);
        for(register int i=1; i<=n; ++i)
            read(a[i]), E.push_back(a[i]);
        sort(E.begin(), E.end());
        E.erase(unique(E.begin(), E.end()), E.end());
        for(register int i=1; i<=n; ++i)
            update(1, n, root[i], root[i-1], getid(a[i]));
        for(register int i=1; i<=m; ++i){
            read(x), read(y), read(k);
            printf("%d\n", E[query(1, n, root[x-1], root[y], k)-1]);
        }
    }
    return 0;
}