splay学习笔记

开始前先放个卿学姐的视频链接：https://www.bilibili.com/video/av6648219?from=search&seid=2858898196423073520）

对于平衡树我先设几个结构体与数组数值

int root;　      　     ///记录根节点
int tot;　　            ///记录下一个节点要存在数组的第几位
int fa[N];             ///记录这个节点的父亲值
struct Node{
　　int siz;           ///记录以这个节点为根的子树的大小
　　int son[2];        ///记录这个节点左右儿子的位置 
　　int val;           ///记录当前节点保存的权值
　　void init(int w){  ///这个函数是为了快速初始化一个节点
　　　　val=w;siz=1;
　　　　son[0]=son[1]=0;
　　}
}T[N];                ///开N个节点

旋转（单旋【左旋、右旋】、双旋）：

　　splay的核心就是旋转，通过旋转让整棵树能尽量保持在log级别的高度；

　　只拿单旋来说明的话：一个节点在他父亲节点的左边就右旋，反之同样；（先别在意单旋是什么东西）

　　zig（右旋）：将x旋转至y

》》》》》》》

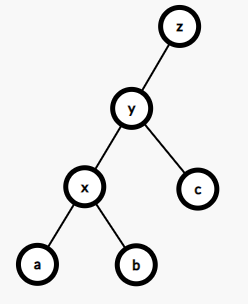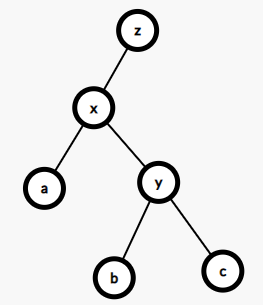
　　　　这个就是简单的右旋，你会发现我们要考虑的内容其实就是：

　　　　1、将z的儿子、x的父亲进行修改；

　　　　2、对x的右节点、x的右节点的父亲进行修改；

　　　　3、对y节点的父亲以及y节点的左儿子进行修改；

　　　　ps：这里加红的字会在下面左旋操作里进行文字说明并对比。

　　zag（左旋）：将x旋转至y

》》》》》》》

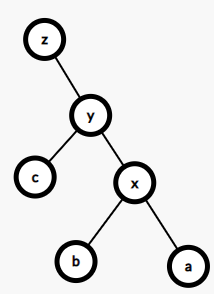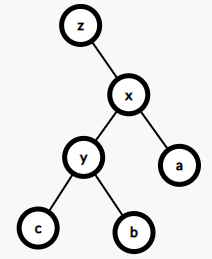
　　　　左旋的内容：

　　　　1、将z的儿子、x的父亲进行修改；

　　　　2、对x的左节点、x的左节点的父亲进行修改；

　　　　3、对y节点的父亲以及y节点的右儿子进行修改；

　　　　好的，和上面右旋相比是不是发现除了左右字眼，其他都没变！！！记住这个结论，这个是我们写Rotate函数(旋转操作)的重要依据，因为这个结论我们可以缩减大量的代码！

///这个是一个基础操作，先在这里贴出来
void pushup(int x){////更新以这个点为根的树的size，就是左右加自己
    T[x].siz=1;
    if(T[x].son[0]){
        T[x].siz+=T[T[x].son[0]].siz;
    }
    if(T[x].son[1]){
        T[x].siz+=T[T[x].son[1]].siz;
    }
}

void Rotate(int x, int kind){///将x旋转 右旋为1
    int y=fa[x];
    int z=fa[y];
    T[y].son[!kind]=T[x].son[kind]; fa[T[x].son[kind]]=y;
    ///操作x点的b节点和y点的关系
    T[x].son[kind]=y; fa[y]=x;
    ///操作x点和y点的关系
    T[z].son[T[z].son[1]==y]=x; fa[x]=z;
    ///操作x点和z点的关系
    pushup(y);///看看上面的关系变动你会发现变动了大小的只有y和x，但是我们现在就更新个y，至于为什么，等一下splay函数里有解释
}

　　我们知道zig和zag的工作原理以后会浮现出一个问题、如下图(将e转到b，一次性画出结果，过程的话自己可以一步步模拟，加深对上面zig、zag的理解)：

　　》》》》》》》》》

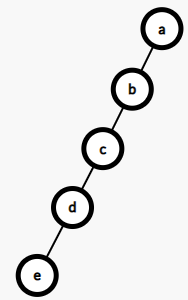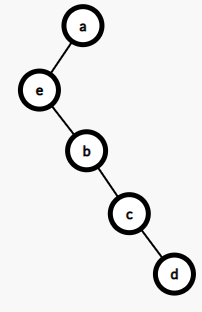
　　这个变换很明显的一个问题就是树的深度完全没变，这是为什么呢！！这里就涉及到了上面挖的坑了！！

　　单旋：就是基础的zig、zag，也就是如果当前节点在父节点的左边，那么我就zig，反之亦然；

　　双旋：每次旋转时候选3个点出来，x，x父亲(y)，y的父亲(z)；然后先将y旋转至z，再将x旋转到y

　　下面还是对上面这个情况，我们用双旋来将它再旋一次、这次我会拆解第一次旋转：

　　取出e,d,c,先旋d,c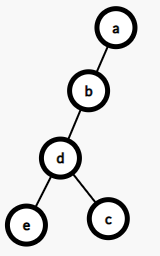再旋e,d

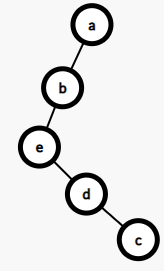
　　好家伙、完全没用，说好的降低深度呢！！！

　　但其实这只不过是一个意外，第一次而已，后面还有几步！！让我们来直接得到结果图吧！！

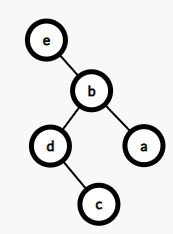这个就是结果，树的高度确实变小了；这个地方的结论也要记住，这个是我们写splay函数(将x旋转至goal)的重要依据；

void Splay(int x, int goal){　　　　///这里要再次声明，spaly是将x转到goal的子节点处
    if(x==goal) return ;
    while(fa[x]!=goal){
        int y=fa[x];
        int z=fa[y];
        int RX=T[y].son[0]==x;　　 ///记录x的操作是要左旋还是右旋，Fa的左节点等于x，那么就是x在Fa的左边，那么就要将x右旋才能向上跑，对吧！
        int RY=T[z].son[0]==y;    ///同理
        if(z==goal){　　　　　　　　 ///这个情况只要根据所得到的RX来旋转x就好了,因为我们在这个循环里的操作是为了将x旋转到goal的其中一个子节点
            Rotate(x, RX);
        }else{　　　　　　　　　　　　///要先转Fa点、因为是双旋
            if(RX==RY){　　　　　　 ///说明x和Fa点都在GrandFa的其中一边，且x也在Fa点的那一边， 假设都在左边，那么就是要把x右旋右旋操作到GrandFa
                Rotate(y, RY);
            }else{　　　　　　　　　 ///这里就是相当于x在Fa的左节点，但Fa在GrandFa的右节点，这个情况就要右旋左旋
                Rotate(x, RX);
            }
            Rotate(x, RY);
        }
    }
    pushup(x);　　　　　　　　　　　　///因为我们会在Rotate的时候沿途更新和x交换的节点的siz，所以说我们现在只要更新x的size
    if(goal==0) root=x;
}

在这里我先甩下一句：Splay的核心就转转转来减少树的高度，没事转一转，大部分时候可以减少被卡时间的风险，比如找个数，找到顺便转一转，可以看下面的Kth操作和Find操作

现在我们已经将splay的旋转部分都学完了；

那么接下来我们就该开始建这颗树了，我们的insert操作很简单，就是将一个val值扔到函数里，比当前节点大就把他扔右边节点去，否则就扔左边，相等的情况看你的实际情况，要记录次数就记录，不然就直接结束；

（当然，如果树是空的怎么办，那就将现在这个节点作为根节点插入！！！）

好的，我们已经知道怎么插入了，但是很明显，我又要来说一下这个方案的缺点了！！！对于下面这个数据你们会怎么插入？num[ ]={1,2,3,4,5,6,7,8,9,10,,,,,,n}

当然，我们先正常插入吧！第一个数直接插入为根，第二个数查一次后插入树里。。。。。。第n个数查询n-1次插入树里，，，，，，妈耶，时间复杂度是多少！！！O((n-1)*n/2)，（#挠头）我还不如直接暴力算了！！

那么为了解决这样的数据我们该怎么办呢！你会发现要是我最后一次插入的数存在根的话，复杂度会变成O(1e6)，那么我们每次旋转当前插入的树为根，这样旋转最长的长度也才logn，均摊的话插入操作复杂度是O(nlogn)；很棒！！那么又来了，记住这个结论，这个是我们写Insert函数(插入数据)的必备优化；

void Insert(int &t, int val, int Pa=0){///int &t我们一般的传入参数是root，即Insert(root, val)[这里真的没有少写参数];   int Pa=0即不传入参数的情况下，Pa默认等于0
    if(t==0){///假设我们现在插入一个数，就应该是Insert(root, val, 0);这样书写，那么也就是说，如果我还没一个节点的时候，root肯定是0(因为初始化)，那么就要直接插入，其他情况也要用到这个，我们下面再说
        t=++tot;///给新建节点一个位置;
        T[t].init(val);///初始化这个节点
        fa[t]=Pa;
        Splay(t, 0);///这个就是刚刚的那个优化技巧
    }else{
        Pa=t;
        if(val<T[t].val) Insert(T[t].son[0], val, Pa);///这里只将他下放到子节点，因为子节点初始化过，所以说肯定为0，也就是传入参数为0，然后就可以用到上面的那个新建节点的操作了
        else if(val>T[t].val) Insert(T[t].son[1], val, Pa);///这里这样写是为了不将相同的数插入，但是再加上一个else就可以实现将这个数字的出现次数++的操作了
        pushup(Pa);///更新一下树的节点大小
    }
}

我们既然已经可以建成一颗树了，那么我们就要用到平衡树的功能之第k大了！！

很明显，我们会发现，对于一颗平衡树，我们常常写的是找第k小，实际意义是找出有多少个数比他小，也就是插入1、2、3，找k=0就是1，以此类推；

也就是说，我们可以根据一点的左儿子的size（以这个节点为根节点的树的大小）来找有多少个数比当前的数小；我们根据代码来解释吧！

int Kth(int k){                    ///现在是求第k小， Kth(T[root].siz-k)是求第k大
    int now=root;
    while(T[T[now].son[0]].siz!=k){///如果刚刚好有k个数比他小的话就直接是根节点
        if(k<T[T[now].son[0]].siz){///如果比这个节点小的数大于k个
            now=T[now].son[0];     ///继续向左子树移动
        }else{                     ///如果比这个节点小的数不足k个，那么我们就要往右边更大的数跑，但是我们发现，这个k其实包括了左子树的size和当前根节点，也就是其实我们已经和这些点确认过了，你不是我要找的点，但是如果继续往右跑，右子树的size肯定会变小，那么就把已经不可能回去的部分减去从右节点开始求新的k的第k大就好了
            k-=T[T[now].son[0]].siz+1;
            now=T[now].son[1];
        }
    }
    Splay(now, root);　　　　　　　　///这里其实和Insert里的优化一样，如果我无限访问一个最深的节点，那不是很浪费时间，于是就直接将他旋转上去，也就是没事转一转
    return T[now].val;
}

已经有了第k大的数的函数了，那我们就来写一下一个数是第几大的函数吧！首先，一个数传入，比当前节点大就去右子树找，并将当前节点转换为他的右节点，找到了这个节点就退出，然后将他旋转到根，看他的左子树有多少个节点来判断他的大小

int Find(int now, int val, int &Rank){
    Rank=1;
    while(T[now].val!=val){
        if(T[now].val>val){
            if(T[now].son[0]){
                now=T[now].son[0];
            }else{///没找到的操作
                
            }
        }else if(T[now].val<val){
            if(T[now].son[1]){
                now=T[now].son[1];
            }else{///没找到的操作
                
            }
        }
    }
    Splay(now, 0);
    if(T[root].son[0]){
        Rank+=T[T[root].son[0]].siz;
    }
    return T[now].val;
}

接下来我们来讲讲splay的删除节点操作，这个操作是删除根节点，也就是如果要删除一个点你要找到(Find函数)这个节点的位置并将他旋转到根；

我们来讨论一下根节点的性质：对于根节点，他左边没有一个节点比他大，他右边没有一个节点比他小；也就是如果要替换这个根，我们就要用左子树的最大值或者右子树的最小值去替换他；

那删除节点的操作（用左子树的最大值替换根）就是找到(Find(root, val))节点k将他旋转为根(Splay(k, 0))，找到左子树的最大值(循环直接找)的节点x，将x旋转为k的子节(Splay(x, k))，模拟替换过程；下面看代码

void Delete( ){
    if(!T[root].son[0]){///先判断有没有左子树，没有直接换根
        fa[T[root].son[1]]=0;
        root=T[root].son[1];
    }
    else{
        int now=T[root].son[0];
        while(T[now].son[1]) now=T[now].son[1];///左子树最大值的节点位置
        Splay(now, root);///将左子树最大值的节点转到根节点的儿子处

        /**下面就是模拟替换过程，因为now是左子树的最大值，而且他旋转到根节点处也只能变成左节点，因为他不可能比根大，所以说他是根的左儿子，但是因为他是左子树里最大的所以说他没有右子树，也就是此时我们就可以将now设为根节点，将原来根节点的右子树直接接上now的右节点**/
        T[now].son[1]=T[root].son[1];///将空的有节点接上根的左子树并删除根
        root=now,fa[now]=0,fa[T[root].son[1]]=root;///不理解就画个图模拟一下
        pushup(root);
    }
}

前驱和后继什么的，基本上就是找比这个数小/大的下一个数，那么我们可以用Find找val是第k大，再找k+1大是谁，或k-1大是谁来解决，我就不多写了！！！！

以上就是以点权为主键的splay；

接下来我们来讲讲以下标为主键的splay（就是支持区间操作的）：

看视频吧！！！！！卿学姐的视频里讲的就是这样的，那个找第k大的性质和上面讲的不太一样，你们只要知道，如果是求一堆数字的第k大的时候就用以点权为主键的splay，有区间操作就用以下标为主键的splay，当然，两个结合的情况。。。。抱歉，我菜，不会树套树。

接下来就是重要的板子了：(下标版的主函数是用来写了序列终结者）

  1 #include<bits/stdc++.h>
  2 #define lson(x) T[x].son[0]
  3 #define rson(x) T[x].son[1]
  4 #define SIZE(tree) (tree.T[tree.root].siz)
  5 using namespace std;
  6 const int N=1e6+7, INF=0x3f3f3f3f;
  7 struct Splay_Tree{
  8     int root, tot, fa[N];
  9     struct T{
 10         int siz, son[2], val, lazy, maxn;
 11         int rev;
 12         void init(int v){
 13             val=maxn=v;siz=1;
 14             son[0]=son[1]=rev=lazy=0;
 15         }
 16     }T[N];
 17     void init(){
 18         tot=root=1;
 19         T[1].init(-INF);
 20     }
 21     void pushup(int x){///更新以这个点为根的树的size
 22         T[x].siz=1;
 23         T[x].maxn=T[x].val;
 24         if(lson(x)){
 25             T[x].maxn=max(T[T[x].son[0]].maxn, T[x].maxn);
 26             T[x].siz+=T[T[x].son[0]].siz;
 27         }
 28         if(rson(x)){
 29             T[x].maxn=max(T[rson(x)].maxn, T[x].maxn);
 30             T[x].siz+=T[rson(x)].siz;
 31         }
 32     }
 33     void pushdown(int x){
 34         if(x==0) return ;
 35         if(T[x].lazy){
 36             if(lson(x)){
 37                 T[lson(x)].val+=T[x].lazy;
 38                 T[lson(x)].maxn+=T[x].lazy;
 39                 T[lson(x)].lazy+=T[x].lazy;
 40             }
 41             if(rson(x)){
 42                 T[rson(x)].val+=T[x].lazy;
 43                 T[rson(x)].maxn+=T[x].lazy;
 44                 T[rson(x)].lazy+=T[x].lazy;
 45             }
 46             T[x].lazy=0;
 47         }
 48         if(T[x].rev){
 49             if(lson(x)) T[lson(x)].rev^=1;
 50             if(rson(x)) T[rson(x)].rev^=1;
 51             swap(lson(x), rson(x));
 52             T[x].rev=0;
 53         }
 54     }
 55     void Rotate(int x, int kind){///将x旋转 右旋为1
 56         int y=fa[x];
 57         int z=fa[y];
 58         T[y].son[!kind]=T[x].son[kind]; fa[T[x].son[kind]]=y;
 59         ///操作x点的B节点和y点的关系
 60         T[x].son[kind]=y; fa[y]=x;
 61         ///操作x点和y点的关系
 62         T[z].son[T[z].son[1]==y]=x; fa[x]=z;
 63         ///操作x点和z点的关系
 64         pushup(y);
 65     }
 66     void Splay(int x, int goal){///这里要声明，spaly是将x转到goal的子节点处
 67         if(x==goal) return ;
 68         while(fa[x]!=goal){
 69             int y=fa[x];
 70             int z=fa[y];
 71             pushdown(z), pushdown(y), pushdown(x);
 72             int RX=lson(y)==x;///记录x的操作是要左旋还是右旋，Fa的左节点等于x，那么就是x在Fa的左边，那么就要将x右旋才能向上跑，对吧！
 73             int RY=lson(z)==y;///同理
 74             if(z==goal){///这个情况只要根据所得到的RX来旋转x就好了,因为我们在这个循环里的操作是为了将x旋转到goal的其中一个子节点
 75                 Rotate(x, RX);
 76             }else{///解释为什么要先转Fa点
 77                 if(RX==RY){///说明x和Fa点都在GrandFa的其中一边，且x也在Fa点的那一边， 假设都在左边，那么就是要把x右旋右旋操作到GrandFa
 78                     Rotate(y, RY);
 79                 }else{///这里就是相当于x在Fa的左节点，但Fa在GrandFa的右节点，这个情况就要右旋左旋
 80                     Rotate(x, RX);
 81                 }
 82                 Rotate(x, RY);
 83             }
 84         }
 85         pushup(x);
 86         if(goal==0) root=x;
 87     }
 88     int Kth(int k){///现在是求第k小， Kth(SIZE-k)是求第k大
 89         int now=root;
 90         pushdown(now);
 91         while(T[lson(now)].siz!=k){///这里其实就是在找一个点，这个点满足有k-1个子节点
 92             if(k<T[lson(now)].siz){
 93                 now=lson(now);
 94             }else{
 95                 k-=T[lson(now)].siz+1;
 96                 now=rson(now);
 97             }
 98             pushdown(now);
 99         }
100         Splay(now, root);
101         return now;
102     }
103     void Insert(int &t, int val, int Pa=0){
104         if(t==0){///假设我们现在插入一个数，就应该是Insert(root, val, 0);这样书写，那么也就是说，如果我还没一个节点的时候，root肯定是0，那么就要直接插入，其他情况也要用到这个，我们下面再说
105             t=++tot;///给新建节点一个位置;
106             T[t].init(val);
107             fa[t]=Pa;
108             Splay(t, 0);
109         }else{
110             Pa=t;
111             if(val<T[t].val) Insert(lson(t), val, Pa);///这里只将他下放到子节点，因为子节点初始化过，所以说肯定为0，也就是传入参数为0，然后就可以用到上面的那个新建节点的操作了
112             else if(val>T[t].val) Insert(rson(t), val, Pa);///这里这样写是为了不将相同的数插入，但是再加上一个else就可以实现将这个数字的出现次数++的操作了
113             pushup(Pa);///更新一下树的节点大小
114         }
115     }
116     void splay_lr(int L, int R, int &u, int &v){
117         u=Kth(L-1), v=Kth(R+1);
118         Splay(u, 0);Splay(v, u);
119     }
120     void update(int L, int R, int val){
121         int u, v;
122         splay_lr(L, R, u, v);
123         T[lson(v)].maxn+=val;
124         T[lson(v)].val+=val;
125         T[lson(v)].lazy+=val;
126     }
127     void Rev(int L, int R){
128         int u, v;
129         splay_lr(L, R, u, v);
130         T[lson(v)].rev^=1;
131     }
132     int query(int L, int R){
133         int u, v;
134         splay_lr(L, R, u, v);
135         return T[lson(v)].maxn;
136     }
137     int build(int L, int R){
138         if(L>R) return 0;
139         if(L==R) return L;
140         int mid=(L+R)>>1, sl, sr;
141         lson(mid)=sl=build(L, mid-1);
142         rson(mid)=sr=build(mid+1, R);
143         fa[sl]=fa[sr]=mid;
144         pushup(mid);
145         return mid;
146     }
147     void init(int n){
148         T[0].init(-INF), T[1].init(-INF), T[n+2].init(-INF);
149         for(register int i=2; i<=n+1; ++i) T[i].init(0);
150         root=build(1, n+2), fa[root]=0;
151         fa[0]=0;T[0].son[1]=root;T[0].siz=0;
152     }
153 }tree;
154 int main( ){
155     int n, m, op, v, L, R;
156     scanf("%d%d", &n, &m);
157     tree.init(n);
158     while(m--){
159         scanf("%d%d%d", &op, &L, &R);
160         if(op==1){
161             scanf("%d", &v);
162             tree.update(L, R, v);
163         }
164         if(op==2){
165             tree.Rev(L, R);
166         }
167         if(op==3){
168             printf("%d\n", tree.query(L, R));
169         }
170     }
171 }

splay下标主键版

  1 #include<bits/stdc++.h>
  2 #define SIZE(tree) (tree.T[tree.root].siz)
  3 using namespace std;
  4 const int N=1e6+7, INF=0x3f3f3f3f;
  5 struct Splay_Tree{
  6     int root, tot, fa[N];
  7     struct T{
  8         int siz, son[2], val;
  9         void init(int w){
 10             val=w;siz=1;
 11             son[0]=son[1]=0;
 12         }
 13     }T[N];
 14     void init(){
 15         tot=root=1;
 16         T[1].init(-INF);
 17     }
 18     void pushup(int x){///更新以这个点为根的树的size
 19         T[x].siz=1;
 20         if(T[x].son[0]){
 21             T[x].siz+=T[T[x].son[0]].siz;
 22         }
 23         if(T[x].son[1]){
 24             T[x].siz+=T[T[x].son[1]].siz;
 25         }
 26     }
 27     void Rotate(int x, int kind){///将x旋转 右旋为1
 28         int y=fa[x];
 29         int z=fa[y];
 30         T[y].son[!kind]=T[x].son[kind]; fa[T[x].son[kind]]=y;
 31         ///操作x点的B节点和y点的关系
 32         T[x].son[kind]=y; fa[y]=x;
 33         ///操作x点和y点的关系
 34         T[z].son[T[z].son[1]==y]=x; fa[x]=z;
 35         ///操作x点和z点的关系
 36         pushup(y);
 37     }
 38     void Splay(int x, int goal){///这里要声明，spaly是将x转到goal的子节点处
 39         if(x==goal) return ;
 40         while(fa[x]!=goal){
 41             int y=fa[x];
 42             int z=fa[y];
 43             int RX=T[y].son[0]==x;///记录x的操作是要左旋还是右旋，Fa的左节点等于x，那么就是x在Fa的左边，那么就要将x右旋才能向上跑，对吧！
 44             int RY=T[z].son[0]==y;///同理
 45             if(z==goal){///这个情况只要根据所得到的RX来旋转x就好了,因为我们在这个循环里的操作是为了将x旋转到goal的其中一个子节点
 46                 Rotate(x, RX);
 47             }else{///解释为什么要先转Fa点
 48                 if(RX==RY){///说明x和Fa点都在GrandFa的其中一边，且x也在Fa点的那一边， 假设都在左边，那么就是要把x右旋右旋操作到GrandFa
 49                     Rotate(y, RY);
 50                 }else{///这里就是相当于x在Fa的左节点，但Fa在GrandFa的右节点，这个情况就要右旋左旋
 51                     Rotate(x, RX);
 52                 }
 53                 Rotate(x, RY);
 54             }
 55         }
 56         pushup(x);
 57         if(goal==0) root=x;
 58     }
 59     void Insert(int &t, int val, int Pa=0){
 60         if(t==0){///假设我们现在插入一个数，就应该是Insert(root, val, 0);这样书写，那么也就是说，如果我还没一个节点的时候，root肯定是0，那么就要直接插入，其他情况也要用到这个，我们下面再说
 61             t=++tot;///给新建节点一个位置;
 62             T[t].init(val);
 63             fa[t]=Pa;
 64             Splay(t, 0);
 65         }else{
 66             Pa=t;
 67             if(val<T[t].val) Insert(T[t].son[0], val, Pa);///这里只将他下放到子节点，因为子节点初始化过，所以说肯定为0，也就是传入参数为0，然后就可以用到上面的那个新建节点的操作了
 68             else if(val>T[t].val) Insert(T[t].son[1], val, Pa);///这里这样写是为了不将相同的数插入，但是再加上一个else就可以实现将这个数字的出现次数++的操作了
 69             pushup(Pa);///更新一下树的节点大小
 70         }
 71     }
 72     void Delete( ){
 73         if(!T[root].son[0]){///先判断有没有左子树，没有直接换根
 74             fa[T[root].son[1]]=0;
 75             root=T[root].son[1];
 76         }
 77         else{
 78             int now=T[root].son[0];
 79             while(T[now].son[1]) now=T[now].son[1];///左子树最大值的节点位置
 80             Splay(now, root);///将左子树最大值的节点转到根节点的儿子处
 81 
 82             /**下面就是模拟替换过程，因为now是左子树的最大值，而且他旋转到根节点处也只能变成左节点，因为他不可能比根大，所以说他是根的左儿子，但是因为他是左子树里最大的所以说他没有右子树，也就是此时我们就可以将now设为根节点，将原来根节点的右子树直接接上now的右节点**/
 83             T[now].son[1]=T[root].son[1];///将空的有节点接上根的左子树并删除根
 84             root=now,fa[now]=0,fa[T[root].son[1]]=root;///不理解就画个图模拟一下
 85             pushup(root);
 86         }
 87     }
 88     int Kth(int k){///现在是求第k小， Kth(SIZE-k)是求第k大
 89         int now=root;
 90         while(T[T[now].son[0]].siz!=k){///这里其实就是在找一个点，这个点满足有k-1个子节点
 91             if(k<T[T[now].son[0]].siz){
 92                 now=T[now].son[0];
 93             }else{
 94                 k-=T[T[now].son[0]].siz+1;
 95                 now=T[now].son[1];
 96             }
 97         }
 98         Splay(now, root);
 99         return T[now].val;
100     }
101     int Find(int now, int val){
102         while(T[now].val!=val){
103             if(T[now].val>val){
104                 if(T[now].son[0]){
105                     now=T[now].son[0];
106                 }else{///没找到 具体要怎么弄返回值和操作依据题目
107                     return -1;
108                 }
109             }else if(T[now].val<val){
110                 if(T[now].son[1]){
111                     now=T[now].son[1];
112                 }else{///没找到
113                     return -1;
114                 }
115             }
116         }
117         Splay(now, root);
118         return now;
119     }
120 }TT;

splay点权主键版

posted @ 2018-08-27 14:09 Thanks_up 阅读(322) 评论(0) 编辑收藏举报

刷新页面返回顶部

ThanksUP

splay学习笔记

公告