【图论#02】岛屿系列题（数量、周长、最大面积），flood fill算法的代码实现与优化

岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

思路

flood fill泛洪算法+dfs

首先我们使用两层for循环遍历二维数组grid，当遇到'1'的时候，标记遇到了“岛屿”，此时岛屿数量加1

然后触发dfs，先将当前位置（是'1'）设为'0',在遇到'1'的位置的上下左右搜索。如果碰到'1'，说明该位置仍是目前发现的岛屿的一部分陆地，将其改为'0'，如果碰到'0'就不管，说明该位置是水不是陆地。

上述操作就是flood fill中的“同化”操作

dfs结束后，当前位置的上下左右都变成了'0'（包括当前位置本身），然后for循环会继续向后遍历，直到再次碰到'1'(即陆地)，然后通过一样的方法统计陆地数量并使用dfs同化。

当二维数组grid遍历完成，那么岛屿的数量也就统计完成了。

疑问

以下是解答1，该代码可以通过测试

class Solution {
public:
    int row, col;
    int dx[4] = {-1,0,1,0};//如果记不住，可以假设一个(1,1)，然后通过加减1来确定对应偏移量
    int dy[4] = {0,-1,0,1};
    int numIslands(vector<vector<char>>& grid) {
        int res = 0;
        row = grid.size();//行
        col = grid[0].size();//列
        for(int x = 0; x < row; ++x){//遍历grid，寻找陆地'1'
            for(int y = 0; y < col; ++y){
                if(grid[x][y] == '1'){//找到陆地之后，同化其上下左右四个方向的区域为'0'
                    dfs(grid, x, y);//调用递归实现
                    res++;//记录岛屿数量
                }
            }
        }
        return res;
    }

    void dfs(vector<vector<char>>& grid, int x, int y){
        grid[x][y] = '0'; 
        for(int i = 0; i < 4; ++i){//循环四次，使用偏移量计算出当前位置的上下左右位置的坐标
            int nx = x + dx[i];
            int ny = y + dy[i];
            if(nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == '1'){
                dfs(grid, nx, ny);//这里其实已经给递归设置了结束条件，如果不满足上面的if的话是不会进入递归的
            }
        }
    }
};

下面是我的解答代码，我也使用了同样的思想，但是为什么我的代码会超时

#include <ratio>
class Solution {
public:
    void dfs(vector<vector<char> >& grid, int x, int y, int row, int col){
        //递归终止条件
        if(x < 0 || x >= row || y < 0 || y >= col || grid[x][y] == '0') return;

        //单层处理逻辑
        grid[x][y] = '0';
        dfs(grid, x - 1, y, row, col);
        dfs(grid, x + 1, y, row, col);
        dfs(grid, x, y - 1, row, col);
        dfs(grid, x, y + 1, row, col);
        return;
    }
    int solve(vector<vector<char> >& grid) {
        // write code here
        if(grid.size() == 0) return 0;
        int row = grid.size();
        int col = grid[0].size();
        int res = 0;
        for(int x = 0; x < row; ++x){
            for(int y = 0; y < col; ++y){
                if(grid[x][y] == '1'){
                    res += 1;
                    dfs(grid, x, y, row, col);
                }
            }
        }
        return res;
    }
};

原因

这个主要是代码实现的问题，思路是一样的，都是基于flood fill泛洪算法+dfs实现

我的代码中，递归中遍历的东西太多，加上递归深度比较深，所以出现了栈溢出的问题

例如，在实现flood fill中"同化"操作时，我的代码需要对上下左右进行四次递归才能将所有情况尝试一遍，这就产生了巨大的开销

优化

使用偏移量来简化对四个方向的搜索

用dx和dy数组来表示上下左右四个方向的偏移量。通过对当前位置 (x, y) 分别加上 dx[i] 和 dy[i]，可以得到该方向的相邻位置 (nx, ny)。

		for(int i = 0; i < 4; ++i){
            int nx = x + dx[i];//由当前位置坐标加上偏移量计算得到的上下左右的坐标
            int ny = y + dy[i];
            if(nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == '1'){
                dfs(grid, nx, ny);
            }
        }

这样优化之后，我们只需要循环4次，计算四个方向的坐标，然后每次调用一个递归函数就可以实现对四个方向的搜索

减少了递归深度

举个例子来说明，假设当前位置为 (1, 1)，则根据 dx 和 dy 数组中的元素，可以得到下面四个相邻位置：

• 上方位置：(1 + dx[0], 1 + dy[0]) = (1 - 1, 1 + 0) = (0, 1)
• 左方位置：(1 + dx[1], 1 + dy[1]) = (1 + 0, 1 - 1) = (1, 0)
• 下方位置：(1 + dx[2], 1 + dy[2]) = (1 + 1, 1 + 0) = (2, 1)
• 右方位置：(1 + dx[3], 1 + dy[3]) = (1 + 0, 1 + 1) = (1, 2)

可以看到，通过不同的 dx[i] 和 dy[i] 组合，可以分别表示上下左右四个方向的移动。

其中，dx[0] = -1 代表向上移动，dx[1] = 0 代表向左移动，dx[2] = 1 代表向下移动，dx[3] = 0 代表向右移动。

类似地，dy[0] = 0、dy[1] = -1、dy[2] = 0、dy[3] = 1 分别对应着上下左右四个方向的纵向偏移量。

岛屿周长

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

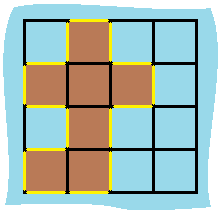
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：

输入：grid = [[1]]
输出：4

示例 3：

输入：grid = [[1,0]]
输出：4

思路

与岛屿数量类似，仍然可以基于flood fill的思想去做，但是我们这里要考虑一些别的事情

同化操作

这里在进行同化时，不能再将方格值修改为0，因为0在题意中是不可遍历的。因此我们可以将同化过的方格标记为2

统计周长

周长如何进行统计呢？其实可以把所有方格可能出现的情况枚举出来即可

假设遍历到当前方格A

• A往某个方向走碰到网格边界，该方向上A的周长加1；
• A往某个方向走碰到水，该方向上A的周长加1；
• A往某个方向走碰到陆地 ，该方向上A的周长不增加；（还没到陆地边界）

代码

代码实现上，仍然使用岛屿数量中的优化版本框架

但是，由于我们需要统计周长，因此dfs需要有返回值

周长统计的几种情况作为递归的结束条件即可

class Solution {
public:
    int row, col;
    int dx[4] = {-1, 0, 1, 0};
    int dy[4] = {0, -1, 0, 1};
    
    int islandPerimeter(vector<vector<int>>& grid) {
        row = grid.size();
        col = grid[0].size();
        int res = 0; // 初始化周长为0
        for (int x = 0; x < row; ++x) {
            for (int y = 0; y < col; ++y) {
                if (grid[x][y] == 1) { // 题目限制只有一个岛屿
                    res = dfs(grid, x, y); // 递归计算岛屿周长
                }
            }
        }
        return res;
    }

    int dfs(vector<vector<int>>& grid, int x, int y) {
        // 从岛屿方格往网格边界走，周长加1
        if (!(x >= 0 && x < row && y >= 0 && y < col)) {
            return 1;
        }
        if (grid[x][y] == 0) {//从岛屿方格往水走，周长加1
            return 1;
        }
        if (grid[x][y] != 1) {//如果当前方格就是水，那么结束递归，因为水无法遍历
            return 0;
        } 
        grid[x][y] = 2; // 将访问过的方格标记为2
        int perimeter = 0;
        for (int i = 0; i < 4; ++i) { // 循环四次，使用偏移量计算出当前位置的上下左右位置的坐标
            int nx = x + dx[i];
            int ny = y + dy[i];
            perimeter += dfs(grid, nx, ny); // 累加周长
        }
        return perimeter;
    }
};

注意：

• dfs中，需要使用周长统计的几种情况作为结束条件

岛屿最大面积

给你一个大小为 m x n 的二进制矩阵 grid。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

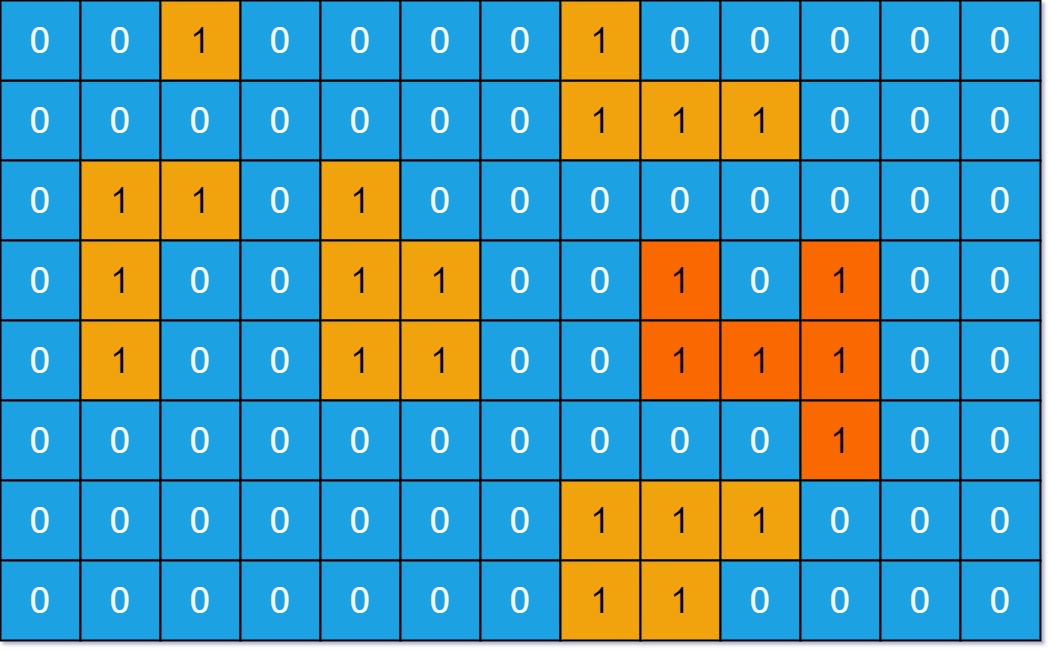
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

思路

因为网格是由多个小格子组成的，每个格子是正方形，因此每个方格的面积是1

因此计算岛屿面积只需要累加遇到的陆地方格的数量即可，所以本题在底层上和岛屿数量是一样的

使用flood fill遍历网格，当遇到陆地时，我们触发递归使其返回当前陆地以及四周区域陆地（如果有）的面积

代码

这里的递归函数也需要返回值，逻辑如下：

如果调用递归函数后发现当前方格是陆地，那么记录当前面积至累加值，然后递归遍历其四周

如果不是陆地，则结束递归

class Solution {
public:
    int dx[4] = {-1,0,1,0};
    int dy[4] = {0,-1,0,1};
    int row, col;
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int res = 0;
        int area = 0;
        row = grid.size();
        col = grid[0].size();
        for(int x = 0; x < row; ++x){
            for(int y = 0; y < col; ++y){
                if(grid[x][y] == 1){
                    area = dfs(grid, x, y);
                    res = max(res, area);
                }
            }
        }
        return res;
    }
    int dfs(vector<vector<int>>& grid, int x, int y){
        if(x >= 0 && x < row && y >= 0 && y < col && grid[x][y] == 1){//遇到陆地触发递归
            grid[x][y] = 0;//同化
            int area = 1;//面积初始值肯定是1
            for(int i = 0; i < 4; ++i){//递归遍历陆地四周
                int nx = x + dx[i];
                int ny = y + dy[i];
                area += dfs(grid, nx, ny); //累加陆地面积
            }
            return area;
        }
        //不是陆地就结束递归
        return 0;
    }
};

注意：这里写dfs时，递归终止条件是当前方格是否是陆地