【图论#01】邻接表的应用以及深度优先搜索
先说一个结论：图论没什么高级的
二叉树也是图的一种，你不是天天见吗。。。
当然，既然图论是一个比二叉树更大的概念，那么二者肯定还是有不同的，详见
不废话了直接上题
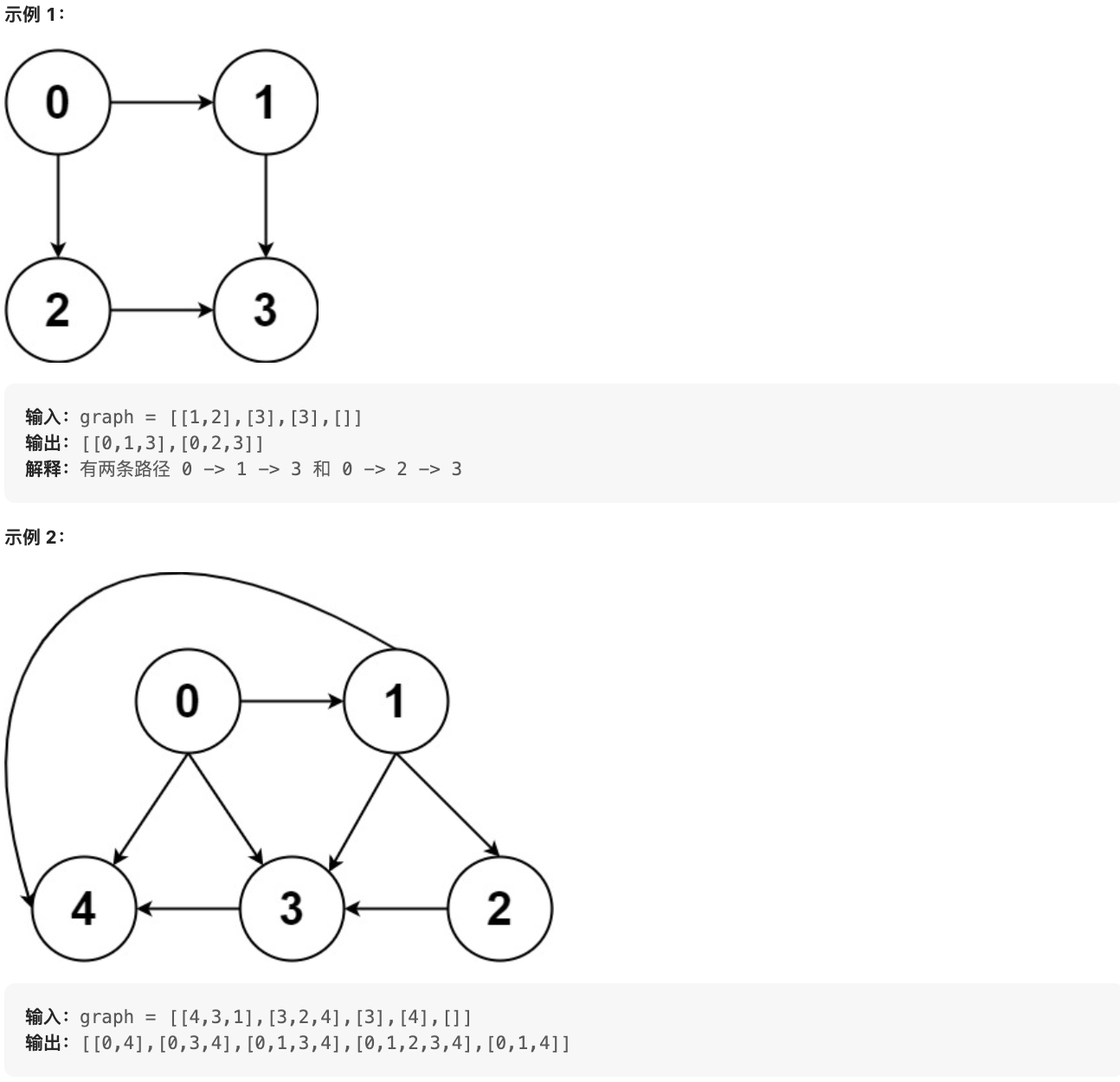
所有可能的路径
给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）
graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。
提示：
- n == graph.length
- 2 <= n <= 15
- 0 <= graph[i][j] < n
- graph[i][j] != i（即不存在自环）
- graph[i] 中的所有元素 互不相同
- 保证输入为 有向无环图（DAG）
在正式做题之前要先补充一些前置知识
知识点：邻接表
图论问题中，我们的操作对象是一个“图”，因此我们需要一个新的数据结构来存放“图”
二叉树可以用ListNode来表示，这是一种特例
邻接表就是一种解决方案
简单来说，邻接表就是一个二维数组，用于保存图中节点之间的关系，这种关系是固定的
为了方便理解，还是以树结构来举例
假设有以下一棵树：
1
/ | \
2 3 4
/ \
5 6
我们可以按照如下方式将这棵树存入graph中：
Codevector<vector<int>> graph;
graph.resize(7); // 根据节点个数创建大小为7的二维向量
graph[1].push_back(2); // 节点1的邻接节点有2
graph[2].push_back(1); // 节点2的邻接节点有1
graph[1].push_back(3); // 节点1的邻接节点有3
graph[3].push_back(1); // 节点3的邻接节点有1
graph[1].push_back(4); // 节点1的邻接节点有4
graph[4].push_back(1); // 节点4的邻接节点有1
graph[3].push_back(5); // 节点3的邻接节点有5
graph[5].push_back(3); // 节点5的邻接节点有3
graph[3].push_back(6); // 节点3的邻接节点有6
graph[6].push_back(3); // 节点6的邻接节点有3
这样，我们就成功地将树的邻接关系存储在了graph中。例如，graph[1]表示节点1的邻接节点列表，其值为{2, 3, 4}，表示节点1与节点2、3、4相邻。
接下来，我们可以使用graph中的数据进行相关操作。比如遍历图的邻接关系：
Codeint node = 1; // 从根节点1开始遍历
for (int neighbor : graph[node]) {
cout << "Node " << node << " is connected to Node " << neighbor << endl;
}
输出结果为：
1 is connected to Node 2
Node 1 is connected to Node 3
Node 1 is connected to Node 4
通过graph可以方便地访问每个节点的相邻节点
思路与代码
有了上述前置知识，现在我们可以使用图论的思想去进行深度优先搜索（dfs）
关于深度优先搜索dfs和广度优先搜索bfs以及它们和前/中/后序遍历的关系简单来说如下：
前/中/后序遍历是dfs在二叉树这种数据结构中的应用；
层序遍历则是bfs在二叉树中的应用。
代码风格和之前回溯的差不多：确定递归函数和参数、确定终止条件、处理单层逻辑
这里我还是像解释一下发生了什么，以官方示例来说
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
graph作为邻接表记录了图的每个节点之间的连接关系
二维数组graph中，每个元素都是一个列表，每个元素的下标对应着一个节点（一共有5个元素，对应从0到4的五个节点）
[4,3,1]代表节点0的连接关系：与节点0直接连接的有节点4、3、1（见示例图）
[3,2,4]代表节点1的连接关系：与节点1直接连接的有节点3、2、4
以此类推
所以邻接表其实是通过元素下标来对应节点，然后节点里面的值又作为索引从邻接表中寻找下一个节点
见下面的代码实现
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void dfs(vector<vector<int>>& graph, int node){
if(node == graph.size() - 1){//确定终止条件
res.push_back(path);
return;
}
//处理单层逻辑，通过传入的参数node确定要遍历的节点列表并开始遍历
for(int i = 0; i < graph[node].size(); ++i){
//取出节点列表中保存的graph[node][i]节点加入path中
path.push_back(graph[node][i]);
//以该节点作为下一层递归的输入参数
dfs(graph, graph[node][i]);
path.pop_back();
}
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
path.push_back(0); // 无论什么路径已经是从0节点出发
dfs(graph, 0);
return res;
}
};
关于ACM下的实际应用，详见https://www.cnblogs.com/DAYceng/p/17614609.html
