【LeetCode回溯算法#extra01】集合划分问题专题【火柴拼正方形、划分k个相等子集、公平发饼干、完成所有工作的最短时间】

火柴拼正方形（相等子集）

https://leetcode.cn/problems/matchsticks-to-square/

你将得到一个整数数组 matchsticks ，其中 matchsticks[i] 是第 i 个火柴棒的长度。你要用 所有的火柴棍 拼成一个正方形。你 不能折断 任何一根火柴棒，但你可以把它们连在一起，而且每根火柴棒必须 使用一次 。

如果你能使这个正方形，则返回 true ，否则返回 false 。

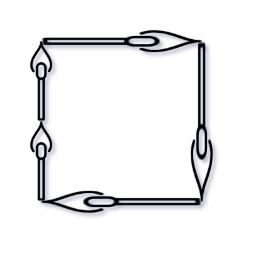
示例 1:

输入: matchsticks = [1,1,2,2,2]
输出: true
解释: 能拼成一个边长为2的正方形，每边两根火柴

示例 2:

输入: matchsticks = [3,3,3,3,4]
输出: false
解释: 不能用所有火柴拼成一个正方形。

提示:

1 <= matchsticks.length <= 15
1 <= matchsticks[i] <= 108

思路

首先，我们需要拼的是一个正方形，那么四边都是相等的，由此我们可以先通过计算火柴数组matchsticks的元素总和（也就是正方形的周长），先判断一下其能不能构成正方形，不能就直接false了

基于此，如果一个火柴数组能够满足构成正方形的基本条件，那再往下讨论

我们可以把正方形的四条边看成四个"边容器"edgeBox

那么问题就变成了：从火柴数组中遍历出值，往edgeBox中放，如果所有的火柴恰好能够放满所有的"边容器"，那么该火柴数组就是可以构成正方形的，过程如下：

在代码实现时，我们可以用一个数组来定义edgeBox，这就是将边看做一个"容器"的原因，即vector<int> edgeBox(4);，正方形就4条边，所以数组大小是固定的

剪枝点：此处例子虽然可以正好用最优的遍历次数解决问题，但很多情况下是会浪费很多时间在“尝试不适合的容器”上的，所以为了尽可能的提高性能，可以先把火柴数组从大到小排序

那么怎么实现上述过程呢？用回溯

代码

回溯分析

还记得回溯怎么写吧?和递归一样，也是三部曲

1、确定回溯函数返回值和参数

根据分析，最终需要返回当前遍历边对应的edgeBox是否装满，所以要返回布尔值

输入参数：matchsticks中火柴的下标stickIndex；matchsticks数组；存放4条边的数组edgeBox；正方形的边长edgeLen

class Solution {
private://确定递归函数的参数与返回值
    //根据分析，最终需要返回当前遍历边对应的edgeBox是否装满，所以要返回布尔值
    //输入参数：stickIndex；matchsticks；edgeBox；edgeLen
    bool traversal(vector<int>& matchsticks, int stickIndex, vector<int>& edgeBox, int edgeLen){
        
    }
public:
    bool makesquare(vector<int>& matchsticks) {
        
    }
};

2、确定终止条件

我们需要通过火柴下标stickIndex来判断递归是否终止，因为本质上我们是用火柴去不断尝试放入edgeBox

如果遍历到最后一根火柴，那么意味着其他火柴都被放到了合适的位置，目前就剩下一个位置给当前的火柴，返回true,结束，此时已经构成了正方形

class Solution {
private://确定递归函数的参数与返回值
    //根据分析，最终需要返回当前遍历边对应的edgeBox是否装满，所以要返回布尔值
    //输入参数：stickIndex；matchsticks；edgeBox；edgeLen
    bool traversal(vector<int>& matchsticks, int stickIndex, vector<int>& edgeBox, int edgeLen){
        //确定终止条件
        //如果遍历到最后一根火柴，就返回true,结束
        if(stickIndex == matchsticks.size()) return true;
    }
public:
    bool makesquare(vector<int>& matchsticks) {
        
    }
};

3、处理单层逻辑

这部分需要不断遍历火柴累加至edgeBox数组的对应位置，并判断当前edgeBox是否"装满"

没装满就继续触发递归（此时还不会运行到返回true的位置），让下一个火柴放入该edgeBox，直到放满或者当前火柴无法放入

不管上述哪种情况，都会触发回溯，将当前火柴拿到edgeBox数组的下一个位置（即下一条边）继续尝试放入

若edgeBox数组遍历结束都没有返回true，那就返回false，说明当前火柴数组不能组成正方形

class Solution {
private://确定递归函数的参数与返回值
    //根据分析，最终需要返回当前遍历边对应的edgeBox是否装满，所以要返回布尔值
    //输入参数：stickIndex；matchsticks；edgeBox；edgeLen
    bool traversal(vector<int>& matchsticks, int stickIndex, vector<int>& edgeBox, int edgeLen){
        //确定终止条件
        //如果遍历到最后一根火柴，就返回true,结束
        if(stickIndex == matchsticks.size()) return true;
        
        //确定单层处理逻辑
        //使用火柴遍历edgeBox
        for(int i = 0; i < edgeBox.size(); ++i){//遍历edgeBox数组
            edgeBox[i] += matchsticks[stickIndex];//试着把火柴放入当前edgeBox
            //做两个判断：1、当前edgeBox是否已经放满；2、当前edgeBox是否能放目前遍历到的火柴
            //没放满（小于等于）就可以继续放
            if(edgeBox[i] <= edgeLen && traversal(matchsticks, stickIndex + 1, edgeBox, edgeLen)) return true;
            edgeBox[i] -= matchsticks[stickIndex];//回溯，如果不能放就把放入的挪走   
        }
        return false;
    }
public:
    bool makesquare(vector<int>& matchsticks) {
        
    }
};

完整代码

在主函数部分，需要计算火柴数组元素和（正方形周长），判断周长是否满足条件

然后进行剪枝操作：对火柴数组进行排序，减少递归次数

步骤：

1、计算火柴数组元素和（正方形周长）

2、判断周长是否满足条件

3、对火柴数组进行排序

4、定义edgeBox数组，调用递归函数

class Solution {
private://确定递归函数的参数与返回值
    bool traversal(vector<int>& matchsticks, int stickIndex, vector<int>& edgeBox, int edgeLen){
        //确定终止条件
        //如果遍历到最后一根火柴，就返回true,结束
        if(stickIndex == matchsticks.size()) return true;

        //确定单层处理逻辑
        //使用火柴遍历edgeBox
        for(int i = 0; i < edgeBox.size(); ++i){
            edgeBox[i] += matchsticks[stickIndex];//试着把火柴放入当前edgeBox
            //做两个判断：1、当前edgeBox是否已经放满；2、当前edgeBox是否能放目前遍历到的火柴
            //没放满（小于等于）就可以继续放
            if(edgeBox[i] <= edgeLen && traversal(matchsticks, stickIndex + 1, edgeBox, edgeLen)) return true;
            edgeBox[i] -= matchsticks[stickIndex];//回溯，如果不能放就把放入的挪走   
        }
        return false;
    }
public:
    bool makesquare(vector<int>& matchsticks) {
        //计算火柴数组元素和（正方形周长）
        int matchstickSum = 0;
        for(auto stick : matchsticks) matchstickSum += stick;

        //判断周长是否满足条件
        if(matchstickSum % 4 != 0) return false;

        //计算正方形边长
        // int edgeLen = matchstickSum / 4;

        //对火柴数组进行排序，减少递归次数
        sort(matchsticks.begin(), matchsticks.end(), greater<int>());//

        //定义一个数组用于表示正方形的四条边
        vector<int> edgeBox(4);//数组大小为4

        //调用递归函数
        return traversal(matchsticks, 0, edgeBox, matchstickSum / 4);
    }
};

题外话：sort内置排序规则

greater表示内置类型从大到小排序，less表示内置类型从小到大排序。

sort(matchsticks.begin(), matchsticks.end(), greater<int>());//从大到小
sort(matchsticks.begin(), matchsticks.end(), less<int>());//从小到大

剪枝

使用 划分k个相等子集 中介绍的剪枝方法可以对本题代码进行优化

优化版代码

class Solution {
private://确定递归函数的参数与返回值
    bool traversal(vector<int>& matchsticks, int stickIndex, vector<int>& edgeBox, int edgeLen){
        //确定终止条件
        //如果遍历到最后一根火柴，就返回true,结束
        if(stickIndex == matchsticks.size()) return true;

        //确定单层处理逻辑
        //使用火柴遍历edgeBox
        for(int i = 0; i < edgeBox.size(); ++i){
            //剪枝优化
            if(i > 0 && edgeBox[i] == edgeBox[i - 1]) continue;

            if(edgeBox[i] + matchsticks[stickIndex] > edgeLen) continue;

            edgeBox[i] += matchsticks[stickIndex];//试着把火柴放入当前edgeBox
            //做两个判断：1、当前edgeBox是否已经放满；2、当前edgeBox是否能放目前遍历到的火柴
            //没放满（小于等于）就可以继续放
            if(edgeBox[i] <= edgeLen && traversal(matchsticks, stickIndex + 1, edgeBox, edgeLen)) return true;
            edgeBox[i] -= matchsticks[stickIndex];//回溯，如果不能放就把放入的挪走   
        }
        return false;
    }
public:
    bool makesquare(vector<int>& matchsticks) {
        //计算火柴数组元素和（正方形周长）
        int matchstickSum = 0;
        for(auto stick : matchsticks) matchstickSum += stick;

        //判断周长是否满足条件
        if(matchstickSum % 4 != 0) return false;

        //计算正方形边长
        // int edgeLen = matchstickSum / 4;

        //对火柴数组进行排序，减少递归次数
        sort(matchsticks.begin(), matchsticks.end(), greater<int>());//

        //定义一个数组用于表示正方形的四条边
        vector<int> edgeBox(4);//数组大小为4

        //调用递归函数
        return traversal(matchsticks, 0, edgeBox, matchstickSum / 4);
    }
};

划分k个相等子集

https://leetcode.cn/problems/partition-to-k-equal-sum-subsets/

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例 1：

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

示例 2:

输入: nums = [1,2,3,4], k = 3
输出: false

提示：

1 <= k <= len(nums) <= 16
0 < nums[i] < 10000
每个元素的频率在 [1,4] 范围内

思路

本题基本上就是 火柴拼正方形 的抽象版，不同的是，火柴那题本质是求 划分4个相等子集 ，而本题将需要划分的子集个数拓展到了k个

好消息是，这两题的思路基本可以复用；坏消息是，采用一般的递归回溯方式解本题会超时

因此，需要引入一些剪枝操作来降低处理成本

所以，这里会侧重讨论剪枝的细节

基本思路再过一遍：

​ 1、先求出待划分数组的元素总和，除以k，判断是否能够继续进行划分

​ 2、若数组元素总和能够均分为k个子集，那么就遍历待划分数组元素，不断尝试放入子集数组中（过程使用递归回溯实现）

​ 3、当待划分数组元素遍历结束，划分完成

代码

回溯分析

1、确定回溯函数的参数与返回值

和火柴那题一样，返回值是布尔，参数是：待划分数组nums、待划分数组遍历下标numsIndex，子集数组subBox，子集长度subLen

class Solution {
private://确定递归函数参数和返回值
    bool traversal(vector<int>& nums, int numsIndex, vector<int>& subBox, int subLen){
        
    }
public:
    bool canPartitionKSubsets(vector<int>& nums, int k) {        
    }
};

2、确定终止条件

终止条件也是一样的：当待划分数组遍历下标numsIndex遍历至最后一个元素，就结束。

class Solution {
private://确定递归函数参数和返回值
    bool traversal(vector<int>& nums, int numsIndex, vector<int>& subBox, int subLen){
        //确定终止条件
        if(numsIndex == nums.size()) return true;
        
    }
public:
    bool canPartitionKSubsets(vector<int>& nums, int k) {        
    }
};

3、确定单层处理逻辑

这里是重点了，虽然逻辑是可以直接套用火柴那题的，但是需要做一定的剪枝才能ac

剪枝点1：如果当前subBox内的值与上一个subBox内的值相同，则可以跳过

什么意思呢？

subBox数组记录的是什么？是当前某个子集中放了多少元素，总和为多少。

该剪枝点会在以下情况被触发：

​ 一个待划分数组的遍历值经过尝试无法放入当前subBox位置（例如subBox[2]），正在尝试subBox中的下一个位置（例如subBox[3]）

如果下一个位置（例如subBox[3]）所记录的元素总和等于上一个位置（例如subBox[2]）的，那么其实该元素还是放不进，因此就没有必要再去执行下面 "尝试放入数组" 的操作了，可以直接去试subBox的下一个位置，从而提高了性能

除此之外，该剪枝点还将另外一种情况也给优化了，即：第一个待划分数组的遍历值放入subBox时，由于subBox元素均为0，所以放哪个都行，不用再去选择了，直接令其放在第一个，这样又节约了一些开销

剪枝点2：提前计算一下放入当前待划分数组遍历值后，subBox对应位置的大小，如果超过我们需要的子集大小（subLen），那也可以直接跳过，不再进行后续的递归判断

class Solution {
private://确定递归函数参数和返回值
    bool traversal(vector<int>& nums, int numsIndex, vector<int>& subBox, int subLen){
        //确定终止条件
        if(numsIndex == nums.size()) return true;

        //确定单层处理逻辑
        //用nums中的值去遍历子集数组，尝试放入
        for(int i = 0; i < subBox.size(); ++i){
            //剪枝点1
            if(i > 0 && subBox[i] == subBox[i - 1]) continue;
			
            //剪枝点2
            if(subBox[i] + nums[numsIndex] > subLen) continue;

            subBox[i] += nums[numsIndex];
            if(subBox[i] <= subLen && traversal(nums, numsIndex + 1, subBox, subLen)) return true;
            subBox[i] -= nums[numsIndex];
        }
        return false;
    }
public:
    bool canPartitionKSubsets(vector<int>& nums, int k) {

    }
};

本质上，此处的剪枝操作都是在递归判断之前，人为的筛选掉一些情况，减少触发递归的次数，进而提升性能

完整代码

主函数部分的逻辑与火柴那题完全一致，就不多说了

class Solution {
private://确定递归函数参数和返回值
    bool traversal(vector<int>& nums, int numsIndex, vector<int>& subBox, int subLen){
        //确定终止条件
        if(numsIndex == nums.size()) return true;

        //确定单层处理逻辑
        //用nums中的值去遍历子集数组，尝试放入
        for(int i = 0; i < subBox.size(); ++i){
            //剪枝点1：
            if(i > 0 && subBox[i] == subBox[i - 1]) continue;
			
            //剪枝点2
            if(subBox[i] + nums[numsIndex] > subLen) continue;

            subBox[i] += nums[numsIndex];//尝试放入待划分数组的遍历值
            if(subBox[i] <= subLen && traversal(nums, numsIndex + 1, subBox, subLen)) return true;
            subBox[i] -= nums[numsIndex];//不满足条件就不能放进来，因此要回溯
        }
        return false;
    }
public:
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        //计算整数数组nums的元素和
        int numSum = 0;
        for(auto num : nums) numSum += num;

        if(numSum % k != 0) return false;

        int subLen = numSum / k;

        //把整数数组从大到小排序
        sort(nums.begin(), nums.end(), greater<int>());

        //创建子集数组
        vector<int> subBox(k);

        return traversal(nums, 0, subBox, subLen);

    }
};

公平发饼干（不相等子集）

https://leetcode.cn/problems/fair-distribution-of-cookies/

给你一个整数数组 cookies ，其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量，所有 零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子，不能分开。

分发的 不公平程度 定义为单个孩子在分发过程中能够获得饼干的最大总数。

返回所有分发的最小不公平程度。

示例 1：

输入：cookies = [8,15,10,20,8], k = 2
输出：31
解释：一种最优方案是 [8,15,8] 和 [10,20] 。

• 第 1 个孩子分到 [8,15,8] ，总计 8 + 15 + 8 = 31 块饼干。
• 第 2 个孩子分到 [10,20] ，总计 10 + 20 = 30 块饼干。
  分发的不公平程度为 max(31,30) = 31 。
  可以证明不存在不公平程度小于 31 的分发方案。

示例 2：

输入：cookies = [6,1,3,2,2,4,1,2], k = 3
输出：7
解释：一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。

• 第 1 个孩子分到 [6,1] ，总计 6 + 1 = 7 块饼干。
• 第 2 个孩子分到 [3,2,2] ，总计 3 + 2 + 2 = 7 块饼干。
• 第 3 个孩子分到 [4,1,2] ，总计 4 + 1 + 2 = 7 块饼干。
  分发的不公平程度为 max(7,7,7) = 7 。
  可以证明不存在不公平程度小于 7 的分发方案。

提示：

2 <= cookies.length <= 8
1 <= cookies[i] <= 105
2 <= k <= cookies.length

思路

本题的核心仍是对数组进行划分，不同的是，这里划分之后的结果可以是一些不相等的子集

但是，需要使这些子集之间的差值尽量的小，即最小不公平程度

这里有个很迷惑的点

因为不公平程度的定义是：单个孩子在分发过程中能够获得饼干的最大总数

也就是说，要达到最小不公平程度，首先需要先将cookies数组尽可能的均分

并且，由于没有规定每个孩子应该获得的饼干数量（即分割后子集的大小），所以像之前两题用的终止条件在本题就不适用了

总结一下，本题需要解决：

​ 如何通过递归回溯去尽可能的均分cookies数组到k个小孩子子集中

先说明一下为什么递归回溯的方式可行

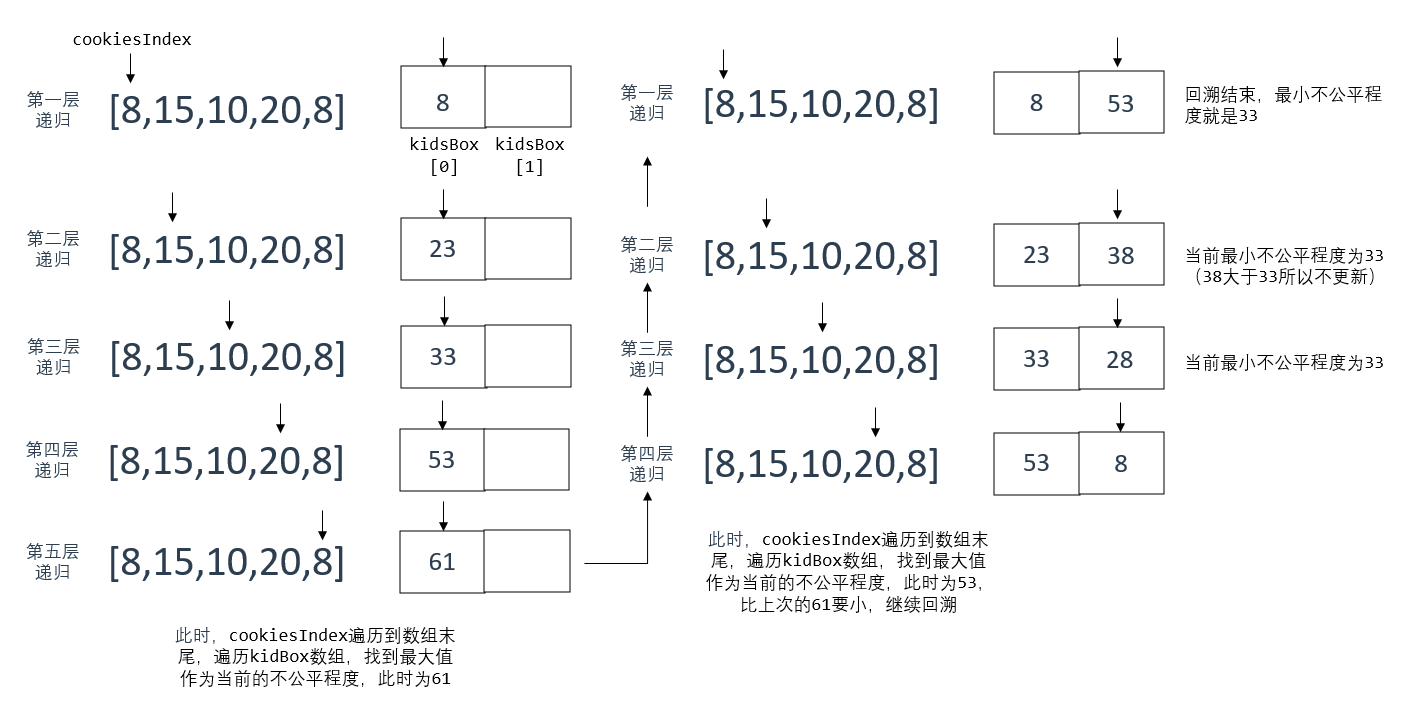
以上是示例1在递归回溯时的全过程

首先，按小朋友个数定义一个kidsBox用于存放分发饼干的累加值

这里的终止条件是饼干数组cookies遍历结束

当遍历下标cookiesIndex到达数组末尾时，我们开始遍历kidsBox，找出当前获得饼干最多的小朋友

将饼干数量更新到用于记录不公平程度的变量并返回

此时触发回溯，从当前层回溯至上一层递归，上一层递归的for循环继续进行下一轮，此时指向kidsBox中的第二个小朋友，累加饼干

（这里又触发了递归，所以又会将for循环卡在第二个小朋友这里，直到cookiesIndex再次到达数组末尾，这个过程很快，以第五层回溯第四层为例，再遍历一次（二号小朋友累加一次）即可触发不公平程度的更新条件）

直到回溯完成，此时记录的不公平程度就是最小的

代码

仍然是按回溯三部曲来写，具体就不拆开写了，直接看代码

使用回溯解决此题也是需要剪枝的，不然必定超时

剪枝点：

1、如果当前小朋友的饼干已经比miniUnfairness多，那就没有必要触发递归再去累加这个小朋友的饼干，因为永远不会是最优值

2、如果当前小朋友的饼干数与上一个小朋友的相同，则跳过当前小朋友，给下一个（同时可以默认将第一包饼干给第一个小朋友）

class Solution {
private:
    int miniUnfairness = INT_MAX;//初始化最小不公平程度变量
    void traversal(vector<int>& cookies, int cookiesIndex, vector<int>& kidsBox){
        //确定终止条件
        //当遍历到饼干数组cookies的最后一个元素时结束，此时遍历小朋友数组kidsBox，找出分得最多饼干的那个人，然后更新miniUnfairness
        if(cookiesIndex == cookies.size()){//遍历到饼干数组末尾
            int tmpMax = INT_MIN;
            for(auto kid : kidsBox){
                if(kid > tmpMax) tmpMax = kid;//找出小朋友数组kidsBox中获得饼干最多的小朋友
            }
            miniUnfairness = min(miniUnfairness, tmpMax);//不断获取最小不公平程度，在数值上，最小不公平程度肯定会先由大变小
            return;
        }
        
        //确定单层处理逻辑
        //注意，每层递归中都有一个for循环，目的是用于处理本层递归的横向遍历过程
        for(int i = 0; i < kidsBox.size(); ++i){
            //剪枝1：如果当前小朋友的饼干已经比miniUnfairness多，那就没有必要触发递归再去累加这个小朋友的饼干，因为永远不会是最优值
            if(kidsBox[i] > miniUnfairness) return;

            //剪枝2：如果当前小朋友的饼干数与上一个小朋友的相同，则跳过当前小朋友，给下一个（同时可以默认将第一包饼干给第一个小朋友）
            if(i > 0 && cookiesIndex == 0) return;

            kidsBox[i] += cookies[cookiesIndex];//尝试将cookiesIndex包饼干给第i个小朋友
            traversal(cookies, cookiesIndex + 1, kidsBox);
            kidsBox[i] -= cookies[cookiesIndex];//本层递归处理完毕，回溯至上一层
        }
        return;
    }

public:
    int distributeCookies(vector<int>& cookies, int k) { 
        vector<int> kidsBox(k);//创建小朋友数组
        sort(cookies.begin(), cookies.end(), greater<int>());//从大到小排序饼干数组
        traversal(cookies, 0, kidsBox);
        return miniUnfairness;
    }
};

完成所有工作的最短时间

https://leetcode.cn/problems/find-minimum-time-to-finish-all-jobs/

给你一个整数数组 jobs ，其中 jobs[i] 是完成第 i 项工作要花费的时间。

请你将这些工作分配给 k 位工人。所有工作都应该分配给工人，且每项工作只能分配给一位工人。工人的 工作时间 是完成分配给他们的所有工作花费时间的总和。请你设计一套最佳的工作分配方案，使工人的 最大工作时间 得以 最小化 。

返回分配方案中尽可能 最小 的 最大工作时间 。

示例 1：

输入：jobs = [3,2,3], k = 3
输出：3
解释：给每位工人分配一项工作，最大工作时间是 3 。

示例 2：

输入：jobs = [1,2,4,7,8], k = 2
输出：11
解释：按下述方式分配工作：
1 号工人：1、2、8（工作时间 = 1 + 2 + 8 = 11）
2 号工人：4、7（工作时间 = 4 + 7 = 11）
最大工作时间是 11 。

提示：

1 <= k <= jobs.length <= 12
1 <= jobs[i] <= 107

思路

和分饼干一模一样，改一下变量名直接ac

代码

虽然可以直接套用分饼干的代码，但是本题在剪枝上应该还有更好的方法，直接套用代码的运行时间大约为476ms，有很大的优化空间

class Solution {
private:
    int costTime = INT_MAX;//初始化最小不公平程度变量
    void traversal(vector<int>& jobs, int jobsIndex, vector<int>& workBox){
        //确定终止条件
        //当遍历到工作数组jobs的最后一个元素时结束，此时遍历工人数组workBox，找出分得最多饼干的那个人，然后更新costTime
        if(jobsIndex == jobs.size()){//遍历到jobs数组末尾
            int tmpMax = INT_MIN;
            for(auto work : workBox){
                if(work > tmpMax) tmpMax = work;//找出工人数组workBox中获得工作时长最多的工人
            }
            costTime = min(costTime, tmpMax);//不断获取最短工作时间，在数值上，最短工作时间肯定会先由大变小
            return;
        }     
        //确定单层处理逻辑
        //注意，每层递归中都有一个for循环，目的是用于处理本层递归的横向遍历过程
        for(int i = 0; i < workBox.size(); ++i){
            //剪枝1：如果当前工人的工作时间已经比costTime多，那就没有必要触发递归再去累加这个工人的工作时间，因为永远不会是最优值
            if(workBox[i] > costTime) return;

            //剪枝2：如果当前工人的工作时间数与上一个工人的相同，则跳过当前工人，给下一个（同时可以默认将第一个工作给第一个工人）
            // if(i > 0 && jobsIndex == 0) return;
            if(i > 0 && workBox[i] == workBox[i-1]) continue;

            workBox[i] += jobs[jobsIndex];//尝试将jobsIndex对应的工作时长给第i个工人
            traversal(jobs, jobsIndex + 1, workBox);
            workBox[i] -= jobs[jobsIndex];//本层递归处理完毕，回溯至上一层
        }
        return;
    }

public:
    int minimumTimeRequired(vector<int>& jobs, int k) {
        vector<int> workBox(k);//创建小朋友数组
        sort(jobs.begin(), jobs.end(), greater<int>());//从大到小排序工作时长数组

        traversal(jobs, 0, workBox);
        return costTime;
    }
};