【LeetCode排序专题02】最小k个数,关于快速排序的讨论
最小k个数
https://leetcode.cn/problems/smallest-k-lcci/
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
限制:
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000
快速排序
快排是一种冒泡法的优化版本,逻辑上使用了分治思想,代码实现上使用了递归的方式,直接上例子来说
以下是一个无序数组,使用快排对其进行排序,核心代码逻辑如右侧所示
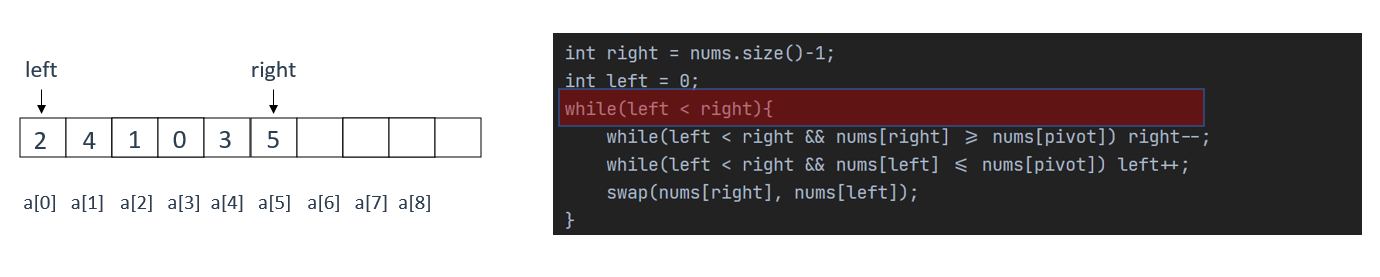
默认以left初始时指向的最左侧元素为基准值
基准值也称为pivot,即"轴"。不断移动左右指针,与轴比较,比轴大的放在轴的右边,比轴小的放在轴的左边
在这里,pivot = 2,即nums[0]
此时满足最外层循环条件,进入循环

大循环内还有两个循环,用于移动左右指针
当前右指针大于基准值pivot(5 > 2),移动right,到3处,还是大,继续移动
到0处不满足条件,执行下一个小循环,判断左指针移动情况

当前左指针等于基准值pivot(2 = 2),满足第二个小循环条件,移动left
此时左指针等于4,大于基准值2,退出小循环,继续执行后面的语句

此时,将左右指针指向的值进行交换
当前左右指针并没有相交,因此继续执行大循环内的两个小循环

(后面的过程同理,就不画图了)
右指针的值还是大于pivot,right左移
此时不满足条件,往后执行第二个小循环
左指针的值小于pivot(0 < 1),left右移
左右指针相交,大循环结束,此时两指针相交的位置就是当前pivot需要移动到的位置

如图所示,pivot(2)移动到相交处
此时,我们就以pivot为基准对数组进行了第一次划分
总结一下过程:
1、先确定基准值,一般用数组最左边的值。
2、然后用右指针和基准值比较,如果右指针指向的值大就不用动当前指向值,向左移动右指针,继续比较,直到右指针指向的值小于基准值(注意,此时还不能交换左右指针值),开始移动左指针
3、使用左指针的值与基准值比较,如果左指针指向的值小就不用动当前指向值,向右移动左指针,继续比较,直到左指针指向的值大于基准值,此时再交换左右指针的值
4、完成一轮移动,如果当前左右指针相交了就结束循环,最左边的基准值和当前相交位置的值互换
5、此时数组被分为左右区间,分别在这两个区间触发递归,继续排序
可见,关键点在于:一定要右指针、左指针都移动完毕之后再交换左右指针指向的值,然后再判断左右指针是否相交
继续
当前,pivot(2)左边的都是小于2的数,pivot(2)右边的都是大于2的数
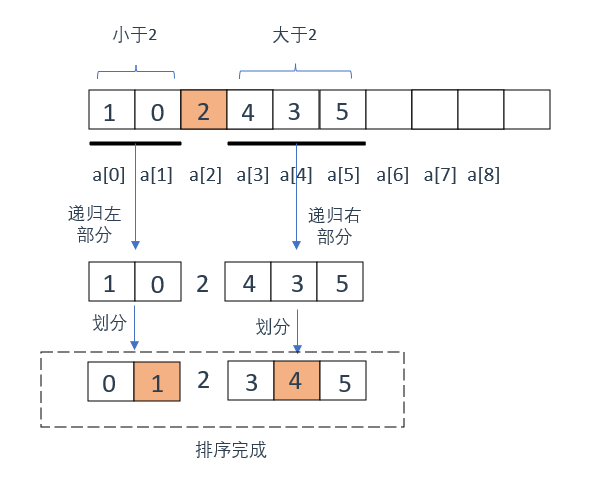
然后,对当前pivot划分的左右区间再次进行划分(方法相同)
这里就是快排需要使用递归的原因,我们需要不断的划分剩余的区间,直到最后排好序
下面来看代码实现
代码分析
凡是涉及递归的都可以按照三部曲来写
1、确认递归函数的参数和返回值
这里是对数组进行排序操作,不需要返回值;
输入参数为待排序的数组以及需要排序的区间
class Solution {
private:
//对数组进行排序操作,不需要返回值,输入参数为待排序的数组以及需要排序的区间
void quickSort(vector<int>& arr, int left, int right){
}
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
}
};
2、确定终止条件
终止条件肯定是左右指针相交
class Solution {
private:
//对数组进行排序操作,不需要返回值,输入参数为待排序的数组以及需要排序的区间
void quickSort(vector<int>& arr, int left, int right){
//确定终止条件
if(left > right) return;
}
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
}
};
3、处理单层递归逻辑
在代码实现时,我们可以直接将left指针指向的值视为pivot(也就是说不用单独定义一个pivot变量,一是影响性能,二是在交换变量时容易逻辑混乱)
循环之前,定义两个循环变量i、j分别初始化为left和right的值
class Solution {
private:
//对数组进行排序操作,不需要返回值,输入参数为待排序的数组以及需要排序的区间
void quickSort(vector<int>& arr, int left, int right){
//确定终止条件
if(left >= right) return;
//处理单层逻辑
//单独定义循环变量
int i = left, j = right;
// int pivot = left;//不用多余再定义一个变量
while(i < j){
//右指针指向的数要大于基准值的话就不用动,仅移动指针(此时,基准值由left充当)
while(i < j && arr[j] >= arr[left]) j--;
while(i < j && arr[i] <= arr[left]) i++;//同理
swap(arr[i], arr[j]);//不满足上述条件就交换
//将right指向的但是小的数放到pivot左边,将left指向的但是大的数放到pivot右边
}//大循环结束,此时左右指针相交,把pivot移动到相交位置
swap(arr[i], arr[left]);//写j也行
//此时已经将数组分为左区间(小于pivot)和右区间(大于pivot)
//调用递归对左右区间再次进行划分,直到排序完成
quickSort(arr, left, i - 1);//左区间递归排序(左指针left重置为数组最左边元素)
quickSort(arr, i + 1, right);//右区间递归(右指针right重置为数组最右边元素)
}
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
}
};
完整代码
class Solution {
private:
//对数组进行排序操作,不需要返回值,输入参数为待排序的数组以及需要排序的区间
void quickSort(vector<int>& arr, int left, int right){
//确定终止条件
if(left >= right) return;
//处理单层逻辑
int i = left, j = right;
// int pivot = left;//不用多余再定义一个变量
while(i < j){
//右指针指向的数要大于基准值的话就不用动,仅移动指针(此时,基准值由left充当)
while(i < j && arr[j] >= arr[left]) j--;
while(i < j && arr[i] <= arr[left]) i++;//同理
swap(arr[i], arr[j]);//不满足上述条件就交换(即右指针、左指针按顺序移动完毕)
//将right指向的但是小的数放到pivot左边,将left指向的但是大的数放到pivot右边
}//大循环结束,此时左右指针相交,把pivot移动到相交位置
swap(arr[i], arr[left]);//写j也行
//此时已经将数组分为左区间(小于pivot)和右区间(大于pivot)
//调用递归对左右区间再次进行划分,直到排序完成
quickSort(arr, left, i - 1);//左区间递归排序(左指针left重置为数组最左边元素)
quickSort(arr, i + 1, right);//右区间递归(右指针right重置为数组最右边元素)
}
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
//调用递归函数
quickSort(arr, 0, arr.size() - 1);
vector<int> res(arr.begin(), arr.begin() + k);//排序后,取数组中"前k大的元素"构成结果数组
return res;
}
};
优化版
这里其实有个可以优化的点
在每次划分完毕后,基准值都会在arr[i]的位置(i为循环变量)
因为题目要求是:返回数组中“前k个最小的数”,只要返回就行,这些数有无顺序均可以
因此可以根据k与i的关系来决定是否继续排序
- 若k < i,代表第 k + 1 小的数字在 左子数组 中,则递归左子数组
- 若k > i,代表第 k + 1 小的数字在 右子数组 中,则递归右子数组
- 若k = i,代表此时
arr[k]即为第 k + 1小的数字,则直接返回数组前 k 个数字即可;
在代码上,需要把递归函数的返回值改为数组,因为要依据i与k的大小关系来决定递归左区间还是右区间,并且,k也需要作为参数输入到递归函数中
TBD


 浙公网安备 33010602011771号
浙公网安备 33010602011771号