【LeetCode排序专题01】由旋转数组的最小数字引出的关于排序算法的讨论（冒泡排序、二分查找+暴力法）
旋转数组的最小数字
剑指 Offer 11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
示例 1：
输入：numbers = [3,4,5,1,2]
输出：1
示例 2：
输入：numbers = [2,2,2,0,1]
输出：0
提示：
n == numbers.length
1 <= n <= 5000
-5000 <= numbers[i] <= 5000
numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转
思路
这题要ac的话其实不难，无非就是对数组进行某种排序，然后返回最小值
本题的价值其实在于讨论各种排序算法
因此，本题可以看成：用哪种排序方法可以更好的把数组排序并返回数组的最小值
冒泡
冒泡法就不用多说了，肌肉记忆了属于是
//冒泡
class Solution {
public:
int minArray(vector<int>& numbers) {
int tmp = 0;
for(int i = 0; i < numbers.size() - 1; ++i){
for(int j = 0; j < numbers.size() - 1 - i; ++j){
if(numbers[j] > numbers[j + 1]){
tmp = numbers[j];
numbers[j] = numbers[j + 1];
numbers[j + 1] = tmp;
}
}
}
return numbers[0];
}
};
这题用冒泡实现虽然能ac，但是性能非常难看（这也是我写这篇记录的原因，因为想尝试其他的排序方法，干脆就一起梳理一下得了）
二分法
二分法其实之前刷代码随想录的时候有用过，但都是用于"查找"某个元素，而不是用来排序
实际上，单纯的使用二分法也不好做到排序
所谓的"二分排序"，更多的是指用二分法+暴力搜索来进行排序
对于本题而言，数组内元素可能有两种情况：无重复值和有重复值
二分法负责"分治"的部分（无重复值），暴力搜索负责在不满足二分条件的情况下对指针进行移动（有重复值）
什么意思呢？下面来讲
数组元素无重复值
一般在进行二分查找的时候有两个要求：
- 顺序存储（通过下标即可得到关键字）
- 元素有序（任取一个关键字的值即可确定target在其前面还是后面）
不论是有无重复值，顺序存储的条件都是满足的，因为都是用数组来保存嘛
无重复值时，元素有序的条件也部分满足，为什么说部分呢？因为旋转后的数组整体上肯定是无序的，但是用于调换的两个部分中的元素还是有序的
例如：
[1,2,3,4,5] -----> [3,4,5,1,2]
[3,4,5] 和 [1,2] 还是有序的
在本题中，所谓的分治，就是对这两个有序部分分开处理，对于有序的元素不再进行排序，而是找到两个有序部分的分界点，逐步将整体变为有序
下面通过一个例子来看
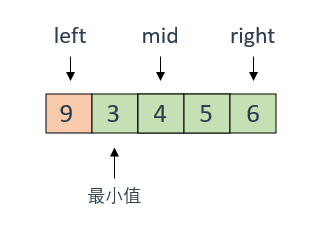
这里定义左右指针以及mid，可以看到，mid指向的值小于right指向的值，即 numbers[mid] < numbers[right]
因为数组是经过旋转而不是打乱的，所以此时可以判定mid后面是有序的，于是移动right到mid的位置，去mid前面找需要排序的元素
此时新的mid为 mid = (right - left)/2 + left
此时，mid还是小于right，说明两个有序部分的交界点还在mid前面，继续去mid前面找
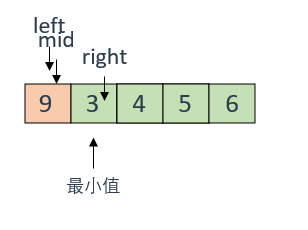
这时，mid大于right了（numbers[mid] < numbers[right]），说明交界点在mid的右边，对右边进行寻找left = mid + 1
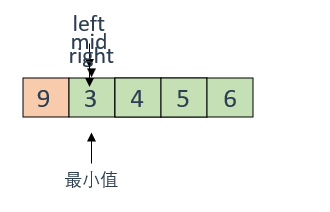
到这一步就触发了二分查找的终止条件，即 left == right ，退出循环，此时就找到了数组中的最小值 numbers[left]（right也行）
以上是数组中没有重复数字的情况
那么有重复数字会怎么样呢？
数组元素有重复值
如果数组中有重复数字，那么可能出现一种特殊情况，即mid指向的值等于right指向的值
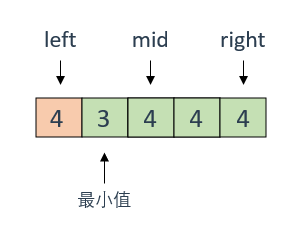
即numbers[mid] = numbers[right]
此时就不能确定分界点在mid的前面还是后面，所以需要暴力法来协助解决
具体来说就是使右指针暴力的从右向左遍历，每次移动一位，同时mid也要相应的移动（还是按之前的公式计算）
直到再次满足mid小于right（移动右指针到mid）或者大于right（移动左指针到mid）的情况，然后使用无重复值时的逻辑（即二分查找）解决即可
代码
class Solution {
public:
int minArray(vector<int>& numbers) {
int left = 0;//设定左右指针
int right = numbers.size() - 1;
if(right == 0) return numbers[0];
while(left < right){
int mid = (right - left)/2 + left;//计算mid值
if(numbers[mid] < numbers[right]){//此时mid右侧是有序的，移动right到mid处，到mid前面找
right = mid;
}else if(numbers[mid] > numbers[right]){//此时mid左侧是有序的，移动left到mid处，到mid后面找
left = mid + 1;
}else{//遇到重复值的情况，右指针从右向左移动
right--;
}
}
return numbers[right];
}
};
