【LeetCode贪心#09】用最少数量的箭引爆气球,无重叠区间,合并区间(涉及区间重叠情况判断与处理)
用最少数量的箭引爆气球
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
- 输入:points = [[10,16],[2,8],[1,6],[7,12]]
- 输出:2
- 解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
- 输入:points = [[1,2],[3,4],[5,6],[7,8]]
- 输出:4
示例 3:
- 输入:points = [[1,2],[2,3],[3,4],[4,5]]
- 输出:2
示例 4:
- 输入:points = [[1,2]]
- 输出:1
示例 5:
- 输入:points = [[2,3],[2,3]]
- 输出:1
提示:
- 0 <= points.length <= 10^4
- points[i].length == 2
- -2^31 <= xstart < xend <= 2^31 - 1
思路
题意理解
题干描述套了一个“打气球”作为背景,搞得有点抽象,其实就是给一个二维数组,寻找里面子数组的重合区间的一个问题
题意图解如下:
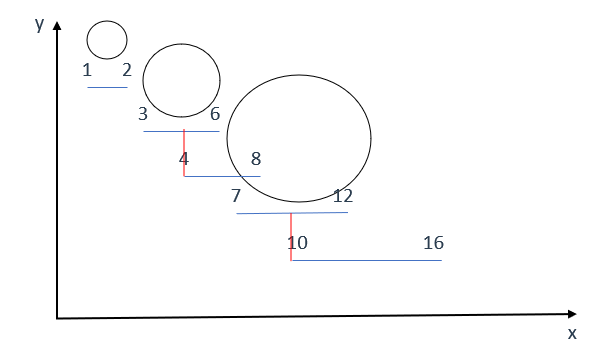
- 输入:points = [[1,2],[3,6],[4,8],[7,12],[10,16]]
- 输出:3
如图所示,[1,2]和[3,6]两个区间所代表的的“气球”没有重合,因此不能同时打爆
而[3,6]和[4,8]位置的两个“气球”是有重合的,因此可以使用一支箭同时打爆
同理[7,12]和[10,16]位置也可以消耗一支箭打爆两个气球,因此要打爆所有气球,最少使用的箭数是3
你可能会想:那为什么不能同时打爆[4,8]和[7,12]位置的气球呢?
如果是上面这种打法,那不重叠的[3,6]和[10,16]区间又分别需要消耗两支箭,导致整体使用箭数不是最少
因此同时打爆[4,8]和[7,12]位置的气球不是最优解
由上述讨论可以得出贪心思路:
局部最优:让重叠区间尽可能多的在一块,好一次打完
全局最优:使用最少的箭打完所有气球
本题难点有两个:
1、如何模拟射气球的过程
2、如何记录重叠数组
过程模拟
模拟射气球时,不需要真的去删除被射中的气球数组,只需计数即可
还是以上面的图为例
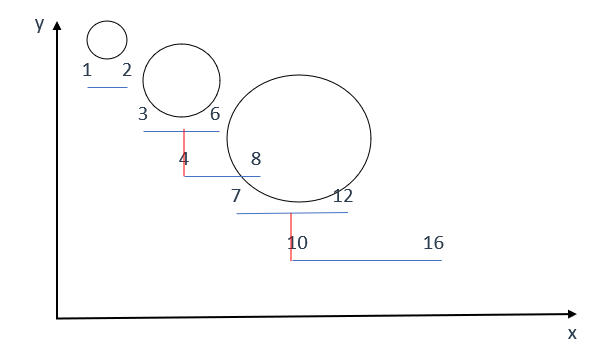
先将所有气球按照左边界排序
情况1:不重叠,需要额外使用箭
以[1,2]和[3,6]为例,[3,6]的左边界3大于[1,2]的右边界2,因此这两个区间无重叠,需要两支箭分别射击,即:
if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2
res++;//使用弓箭数增加
}
情况2:重叠检查并更新右边界
以[3,6]和[4,8]为例,显然这两个位置的气球时重叠的,那肯定就不满足情况1的条件,因此我们可以接着情况1写在else里面
if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2
res++;//使用弓箭数增加
}else{//(points[i][0] <= points[i - 1][1]的情况
}
为什么有等于?因为题目说了挨着的气球也可以一次打爆
当气球有重合时,我们不需要使用新的弓箭。但是如果遍历到下一个区间,它也与之前的区间有重合,我们怎么去处理这种情况?
这个时候就需要在遇到重叠区间时,记录当前最小的右边界以提供给下一个区间进行重叠判断
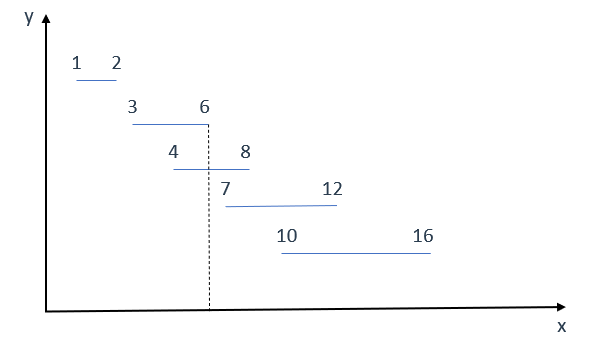
如图所示,当下标i遍历到[4,8]区间时,其与下标为i - 1的[3,6]区间有重合
此时不知道之后会不会还有区间与这两个区间有重合,所以需要记录下这两个区间中最小的那个右边界用于后续判断
最小右边界显然是6,当下标i遍历到[7,12]时,[7,12]的左边界大于当前的最小右边界6
所以[7,12]没有与[3,6]、[4,8]有重叠部分,因此需要额外的弓箭来射击(满足情况1)
所以情况2的代码逻辑如下:
if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2
res++;//使用弓箭数增加
}else{//(points[i][0] <= points[i - 1][1]的情况
points[i][1] = min(points[i - 1][1], points[i][1]);//取两个重合区间中最小的右边界作为当前右边界
}
代码
根据上述分析可以总结出以下步骤:
1、自定义比较规则cmp,按左边界对数组先进行排序
2、判断数组为0的情况
2、初始化弓箭数量变量(注意初始值为1,因为0的情况已经判断过,所以之后的情况至少需要一支弓箭)
3、遍历数组,判断两种情况
- 情况1,无重叠,更新res值记录所需的新弓箭
- 情况2,有重叠,更新最小右边界,即
(points[i] [0] <= points[i - 1] [1]
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b){
return a[0] < b[0];
}
int findMinArrowShots(vector<vector<int>>& points) {
if (points.size() == 0) return 0;//先判断数组为0的情况
//对二维数组进行排序
sort(points.begin(), points.end(),cmp);
int res = 1;//记录弓箭使用数量,因为0的情况已经判断过,所以之后的情况至少需要一支弓箭
//遍历数组
for(int i = 1; i < points.size(); ++i){//从1开始,不然比到最后会有负数
//判断左右边界情况,即重叠情况
if(points[i][0] > points[i - 1][1]){//情况1,无重叠
res++;
}else{//情况2,有重叠,更新最小右边界//(points[i][0] <= points[i - 1][1]
points[i][1] = min(points[i - 1][1], points[i][1]);
}
}
return res;
}
};
无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
- 输入: [ [1,2], [2,3], [3,4], [1,3] ]
- 输出: 1
- 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
- 输入: [ [1,2], [1,2], [1,2] ]
- 输出: 2
- 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
- 输入: [ [1,2], [2,3] ]
- 输出: 0
- 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路
做过射气球那题之后,这题就很好理解了
整体思路无非也是排序(左右边界均可,这里还是和上题保持一致,用左边界)后找出重叠区间,然后进行对应的处理
代码
和上题一样,没意思
步骤:
1、自定义排序
2、定义变量记录需要删除的区间的个数
3、遍历区间,判断重叠情况
- 左边界大于等于右边界(区别于上一题,本题相邻的情况也算作不重叠),无重叠,不进行任何操作
- 左边界小于右边界,区间重叠,当前区间为待删除区间,更新删除区间的数量
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b){
return a[0] < b[0];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
//排序
sort(intervals.begin(), intervals.end(), cmp);
int removeNums = 0;//记录移除区间数量,从1开始
//遍历
for(int i = 1; i < intervals.size(); ++i){
if(intervals[i][0] >= intervals[i - 1][1]){//不重叠,无操作
}else{//区间重叠
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]);//更新当前重叠区间中的最细小右边界的
removeNums++;//记录需要移除的区间
}
}
return removeNums;
}
};
总结
TBD
合并区间
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
- 输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
- 输出: [[1,6],[8,10],[15,18]]
- 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
- 输入: intervals = [[1,4],[4,5]]
- 输出: [[1,5]]
- 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
- 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
思路
大体思路和上两题(气球、无重叠区间)类似,就是找重叠区间,只不过这里找到之后需要进行合并操作
这里如果直接写的话有个坑,就是容易在“合并”操作上搞得很复杂(比如取重叠区间的左右区间重新新建一个区间然后保存)
因为我们在遍历数组之前事先进行了排序,因此我们可以对合并操作进行简化
当遍历到第一个区间时,可以直接将其加入结果集
然后遍历后续区间时,就用结果集内的最后一个区间(刚开始就是第一个区间)的右边界去比较遍历区间的左边界,判断是否重叠。
如果重叠,就更新结果集中区间的右边界(取大的)
如果不重叠,就将遍历区间加入结果集,重复上述过程,直到遍历结束
代码
步骤:
1、对数组进行自定义排序,处理数组为空的情况
2、将第一个区间加入结果集
3、遍历数组,用结果集内的最后一个区间的右边界与当前遍历区间的左边界进比较
- 右边界大于新区间的左边界,有重叠,合并重叠区间(即更新结果集中区间的右边界)
- 无重叠,则将当前区间加入结果集
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b){
return a[0] < b[0];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> res;// 定义结果数组
if (intervals.size() == 0) return res; // 区间集合为空直接返回
sort(intervals.begin(), intervals.end(), cmp);
res.push_back(intervals[0]);// 先将第一个区间加入结果集,如果后面有重叠就直接合并
for(int i = 1; i < intervals.size(); ++i){//从1开始
if(res.back()[1] >= intervals[i][0]){//右边界大于新区间的左边界,有重叠,合并重叠区间
//只更新右边界即可,因为左边界排序了的,一定是最小的
res.back()[1] = max(intervals[i][1], res.back()[1]);
}else{//无重叠,将当前区间加入结果集
res.push_back(intervals[i]);
}
}
return res;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号