【LeetCode二叉树#20】二叉搜索树转换为累加树，巩固二叉树的遍历（特殊的中序遍历）
将二叉搜索树转换为累加树
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。
示例 1：
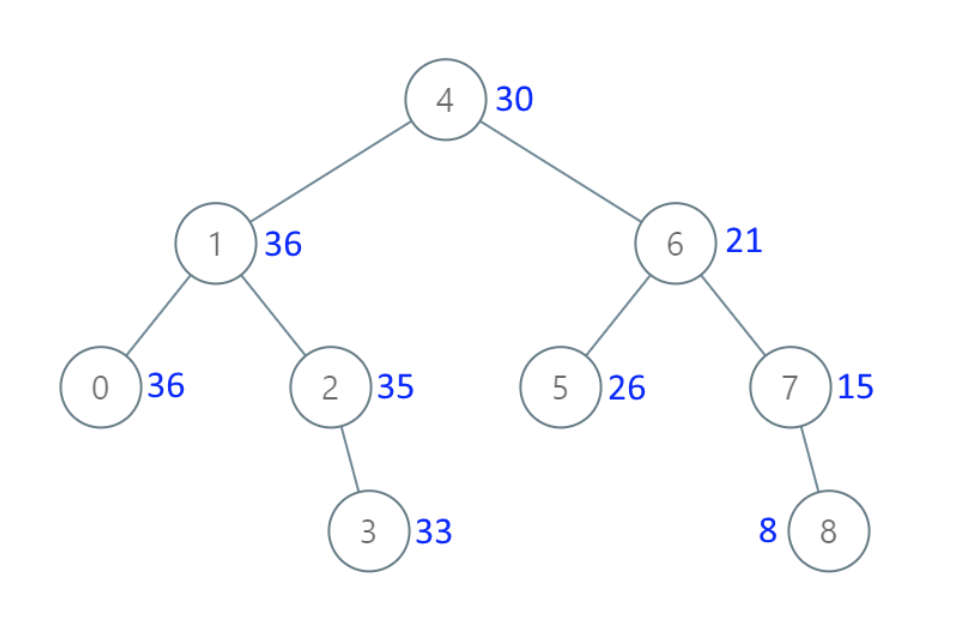
- 输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：
- 输入：root = [0,null,1]
- 输出：[1,null,1]
示例 3：
- 输入：root = [1,0,2]
- 输出：[3,3,2]
示例 4：
- 输入：root = [3,2,4,1]
- 输出：[7,9,4,10]
提示：
- 树中的节点数介于 0 和 104 之间。
- 每个节点的值介于 -104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
思路
题目的意思是从二叉搜索树的右子树的最右边一个节点开始，不断累加前一个节点的值并更新为当前节点的值
感觉就算这么说还是不太好理解
二叉搜索树知道吧？如果按照中序遍历（不记得就看这里）获取到整颗树的节点值，那么将构成一个升序数组
此时，如果我们倒着遍历这个数组并将每个元素前面的值累加到当前值位置，不就完成了题目的要求吗？
举个例子：
一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]
因此，本题中遍历二叉搜索树的顺序应该是右中左，这样得到的结果就是一个降序数组，即从二叉搜索树的右子树的最右边一个节点开始的数组
递归法
先用递归做做
1、确定递归函数参数和返回值
只是要操作一颗二叉树，不涉及回溯返回节点值，不需要返回值
参数是当前节点指针
2、确定终止条件
遍历操作嘛，当前指针指向空就可以停止递归了
3、单层处理逻辑
按照前面讨论的，我们使用右中左的顺序来遍历，目的是得到一个降序的数组
当遍历到中节点时，让当前节点的值累加上前一节点的值即可
class Solution {
public:
int pre = 0;//用于保存前一节点值
//确定递归函数参数和返回值
void traversal(TreeNode* cur){
//确定终止条件
if(cur == NULL) return;
//确定单层处理逻辑
//调用递归
//右
traversal(cur->right);
//中，处理累加逻辑
cur->val += pre;
pre = cur->val;
//左
traversal(cur->left);
}
TreeNode* convertBST(TreeNode* root) {
traversal(root);
return root;
}
};
迭代法
迭代法解的话就是经典模板套用即可，详见
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
//定义栈
stack<TreeNode*> st;
//定义当前指针
TreeNode* cur = root;
//定义变量保存前一节点值
int pre = 0;
//遍历
while(!st.empty() || cur != NULL){
if(cur != NULL){//cur不为空，后面还有数，继续遍历
//压栈
st.push(cur);
cur = cur->right;//右
}else{//为空，说明遍历到了当前分支的叶子节点
cur = st.top();//中，取出节点
st.pop();
cur->val += pre;//累加
pre = cur->val;//记录前一节点值
//判断每个出栈的节点是否有左右子节点
//如果有，则又会触发if的第一个条件，继续将右子节点压栈
cur = cur->left;//左
//不存在的话cur指向空就又来到else这
}
}
return root;
}
};
注意点
从栈中取节点之后别忘了弹出
