【LeetCode二叉树#09】路径总和I+II,以及求根节点到叶节点数字之和(回溯回溯,还是™的回溯)
路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
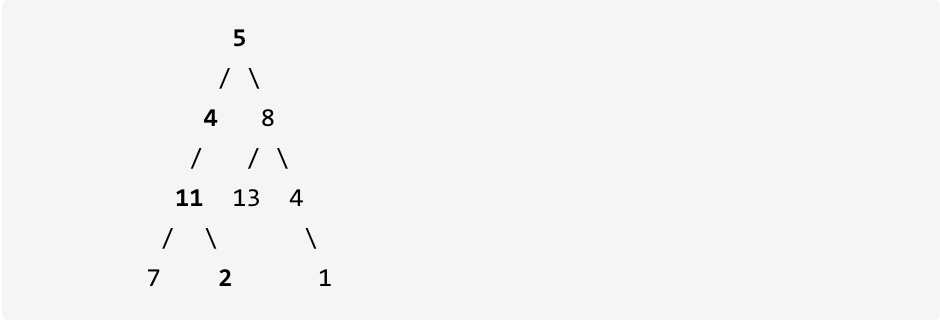
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2
思路
用递归的方法做,传入target值,没遍历到一个节点就与其做差
如果最后遍历到叶子节点时target值变成0,那么就说明本条路径的节点之和满足target值
递归法
1、确定递归函数参数和返回值
输入肯定是根节点了,因为还需要把target传入,所以还需要一个计数变量int count
那么,返回值如何确定?或者说需不需要返回值?
这里引申一个问题:递归函数什么时候需要返回值?
可以总结为如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (236. 二叉树的最近公共祖先 (opens new window))
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
因为题目只要求我们找出一条符合路径值等于target的路径,所以我们有可能不需要完整遍历整颗二叉树。且一旦找到满足条件的路径,需要及时返回
因此递归函数的返回值应该是bool
bool traversal(TreeNode* node, int count){
}
2、确定终止条件
这里要考虑如何统计全部路径节点的值
注意,不要使用累加的方式(即遍历一个节点加一个,然后最后再判断是否满足target),这种方式虽然很容易想到,但是代码实现比较麻烦
因此,我们将count设置为target的大小,让其在递归遍历的过程中递减
那么结束的条件就有以下两种:
1、遇到叶子节点(遍历结束),且当前count已经递减至0
2、遇到叶子节点(遍历结束)但count不为0
bool traversal(TreeNode* node, int count){
if(node->left == NULL && node->right == NULL && count == 0) return true;
if(node->left == NULL && node->right == NULL) return false;
}
3、确定单层处理逻辑
调用递归函数,当我们找到满足条件的路径或者已经到达叶子节点后,需要通过回溯将count值再加回原来的初值状态(等于target)
因为递归函数设置了返回值,如果我们找到符合条件的路径,就可以立刻返回true
没找到就返回false
bool traversal(TreeNode* node, int count){
//确定终止条件
//到叶子节点并找到路径
if(node->left == NULL && node->right == NULL && count == 0) return true;
//到叶子节点但没找到路径
if(node->left == NULL && node->right == NULL) return false;
//确定单层处理逻辑
//调用递归函数
if(node->left){
count -= node->left->val;//不断递减
//如果递归函数返回true,则找到路径,可以直接返回true
if(traversal(node->left, count)) return true;
count += node->left->val;//回溯,撤销处理结果
}
if(node->right){
count -= node->right->val;//不断递减
//如果递归函数返回true,则找到路径,可以直接返回true
if(traversal(node->right, count)) return true;
count += node->right->val;//回溯,撤销处理结果
}
return false;//没找到返回false
}
代码
class Solution {
public:
//使用递归,遍历出所有路径,将路径之和与target比较
//确定递归函数的参数和返回值
bool traversal(TreeNode* node, int count){
//确定终止条件
//到叶子节点并找到路径
if(node->left == NULL && node->right == NULL && count == 0) return true;
//到叶子节点但没找到路径
if(node->left == NULL && node->right == NULL) return false;
//确定单层处理逻辑
//调用递归函数
if(node->left){
count -= node->left->val;//不断递减
//如果递归函数返回true,则找到路径,可以直接返回true
if(traversal(node->left, count)) return true;
count += node->left->val;//回溯,撤销处理结果
}
if(node->right){
count -= node->right->val;//不断递减
//如果递归函数返回true,则找到路径,可以直接返回true
if(traversal(node->right, count)) return true;
count += node->right->val;//回溯,撤销处理结果
}
return false;//没找到返回false
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == NULL) return false;//先判断根节点是否为空
int count = targetSum - root->val;//根节点也算在路径中,所以count也要减去其值
return traversal(root, count);
}
};
迭代法
TBD
注意点
1、在主函数中,必须确认根节点是否为空,否则必错
2、在主函数中,不要忘记把根节点的值加入递减计数
二刷问题
递归函数的停止条件顺序不能互换
class Solution {
public:
//使用递归,遍历出所有路径,将路径之和与target比较
//确定递归函数的参数和返回值
bool traversal(TreeNode* node, int count){
//确定终止条件
//到叶子节点并找到路径
if(node->left == NULL && node->right == NULL && count == 0) return true;
//到叶子节点但没找到路径
if(node->left == NULL && node->right == NULL) return false;
//错误:
//if(node->left == NULL && node->right == NULL) return false;
//if(node->left == NULL && node->right == NULL && count == 0) return true;
这是因为当根节点没有左右子树时,需要特别处理。
在第一个if语句中,如果count等于0,则说明从根节点到叶子节点的路径上所有节点之和正好等于目标值targetSum,因此返回true。在第二个if语句中,如果没有匹配到第一个if语句的条件,则说明到达了叶子节点但是总和不等于目标值targetSum,此时应该返回false,表示没有符合条件的路径。
如果将两个if语句的顺序互换,会导致遍历到叶子节点时无法正确判断是否存在一条符合条件的路径。当叶子节点没有左右子树时,先进入第二个if语句中的条件判断,返回false,而不检查路径和是否等于目标值,因此会误判。
也就是说,到了叶子节点必须先判断一路上的路径值,如果满足条件就要返回true,如果上述代码顺序颠倒,则会把一些正确的满足条件的结果漏掉,直接判断为false,从而导致错误
记得回溯
到当前叶子节点的路径不满足条件时要往回走,记得要再把count加回来,也就是进行回溯操作
路径总和II
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
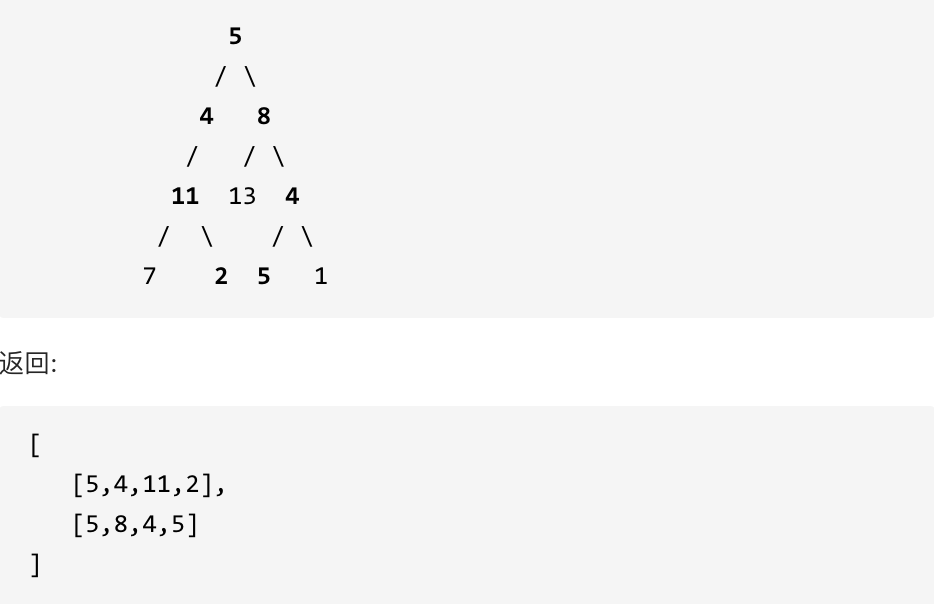
思路
因为题目要求的是返回所有路径节点和满足target的路径
所以,我们需要遍历整棵树
按照前面的讨论,这种情况下,递归函数不需要返回值(因为不需要满足条件就返回)
这里只介绍递归法,迭代法太麻烦了,写了也记不住
本题中,用于存放路径的数组path和存放结果的二维数组res需要定义在递归函数外
1、确定递归函数的参数和返回值
与路径总和的基本思路一致,输入是根节点和一个计数变量(通过递减来寻找满足条件的路径)
返回值是不需要的
2、确定终止条件
终止条件也与路径总和一致,共两种:
- 遇到叶子节点,且路径满足条件
- 遇到叶子节点但不满足条件
3、确定单层逻辑
在这一步中,我们除了对计数变量count进行递减和回溯,还需要将当前节点的值加入路径数组path中,并在回溯时将元素pop掉
代码
class Solution {
public:
vector<vector<int>> res;//存放最值输出结果
vector<int> path;//存放当前满足条件的路径
//确定递归函数的参数和返回值
//输入参数为根节点和计数变量
//本题中,需要找出所有路径节点之和满足条件的路径,因此需要遍历整棵树,故没有返回值
void traversal(TreeNode* node, int count){
//确定终止条件
//遇到叶子节点,且路径满足条件
if(node->left == NULL && node->right == NULL && count == 0){
//保存此时path中记录的路径
res.push_back(path);
return;
}
//遇到叶子节点但不满足条件
if(node->left == NULL && node->right == NULL) return;
//确定单层逻辑
if(node->left){
//保存当前节点值到path
path.push_back(node->left->val);
//计数递减
count -= node->left->val;
traversal(node->left, count);//调用递归
//回溯,包括计数变量和路径数组
count += node->left->val;
path.pop_back();
}
if(node->right){
//保存当前节点值到path
path.push_back(node->right->val);
//计数递减
count -= node->right->val;
traversal(node->right, count);//调用递归
//回溯,包括计数变量和路径数组
count += node->right->val;
path.pop_back();
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
//确认根节点不为空
if(root == NULL) return res;
int count = targetSum - root->val;//将根节点加入递减计数
path.push_back(root->val);//将根节点值加入数组
traversal(root, count);
return res;
}
};
注意点
1、用于存放路径的数组path和存放结果的二维数组res需要定义在递归函数外
2、在主函数中,必须确认根节点是否为空
3、在主函数中,不要忘记把根节点的值加入递减计数,以及路径数组
求根节点到叶节点数字之和
https://leetcode.cn/problems/sum-root-to-leaf-numbers/
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:

输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10
思路
与路径总和II类似,因为要遍历完二叉树的所有路径,因此递归函数无需返回值,只需去操控一个vector即可
在本题中,以何种方式遍历二叉树是无所谓的
下面来三部曲
确定递归函数+终止条件
前面说了,因为要遍历整个树,所以递归函数不需要返回值。显然,其输入是当前节点
class Solution {
private:
void traversal(TreeNode* cur){
if(cur->left == nullptr && cur->right == nullptr){//遍历到叶子节点
res += vec2Int(path);
return;
}
}
public:
int sumNumbers(TreeNode* root) {
}
};
当前节点为叶子节点时,将一路上收集到的各个节点的值(path数组)转换为整数
(注意叶子节点的判断依据:即左右子节点为空)
此时,需要一个辅助函数vec2Int,可以注意一下该函数的实现,这是一种整数转换的方法
class Solution {
private:
int res = 0;
vector<int> path;
int vec2Int(vector<int>& path){//用于处理数组path,将其转换为整数
int sum = 0;
for(int i = 0; i < path.size(); ++i){
sum = sum*10 + path[i];
}
return sum;
}
void traversal(TreeNode* cur){
if(cur->left == nullptr && cur->right == nullptr){//遍历到叶子节点
res += vec2Int(path);
return;
}
}
public:
int sumNumbers(TreeNode* root) {
}
};
确定单层处理逻辑
这里就跟路径总和II的处理方式一样了,先判断左右子节点是否存在,如果存在就将其值加入路径数组
class Solution {
private:
int res = 0;
vector<int> path;
int vec2Int(vector<int>& path){//用于处理数组path,将其转换为整数
int sum = 0;
for(int i = 0; i < path.size(); ++i){
sum = sum*10 + path[i];
}
return sum;
}
void traversal(TreeNode* cur){
if(cur->left == nullptr && cur->right == nullptr){//遍历到叶子节点
res += vec2Int(path);
return;
}
if(cur->left){//递归遍历左分支
path.push_back(cur->left->val);
traversal(cur->left);
path.pop_back();
}
if(cur->right){//递归遍历右分支
path.push_back(cur->right->val);
traversal(cur->right);
path.pop_back();
}
return;
}
public:
int sumNumbers(TreeNode* root) {
}
};
注意记得回溯
代码
class Solution {
private:
int res = 0;
vector<int> path;
int vec2Int(vector<int>& path){//用于处理数组path,将其转换为整数
int sum = 0;
for(int i = 0; i < path.size(); ++i){
sum = sum*10 + path[i];
}
return sum;
}
void traversal(TreeNode* cur){
if(cur->left == nullptr && cur->right == nullptr){//遍历到叶子节点
res += vec2Int(path);
return;
}
if(cur->left){//递归遍历左分支
path.push_back(cur->left->val);
traversal(cur->left);
path.pop_back();
}
if(cur->right){//递归遍历右分支
path.push_back(cur->right->val);
traversal(cur->right);
path.pop_back();
}
return;
}
public:
int sumNumbers(TreeNode* root) {
if(root == nullptr) return 0;
path.push_back(root->val);//不要忘了先把当前节点压入数组
traversal(root);
return res;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号