【LeetCode二叉树#07】左叶子节点之和(基于栈的迭代法前中后序遍历复习)
左叶子节点之和
计算给定二叉树的所有左叶子之和。
示例:

思路
注意审题,这里是要求 左叶子节点 之和
不是二叉树中的左侧节点之和,因此使用层序遍历是不合适的
我们要明确的是,到底什么是左叶子节点
举个例子:
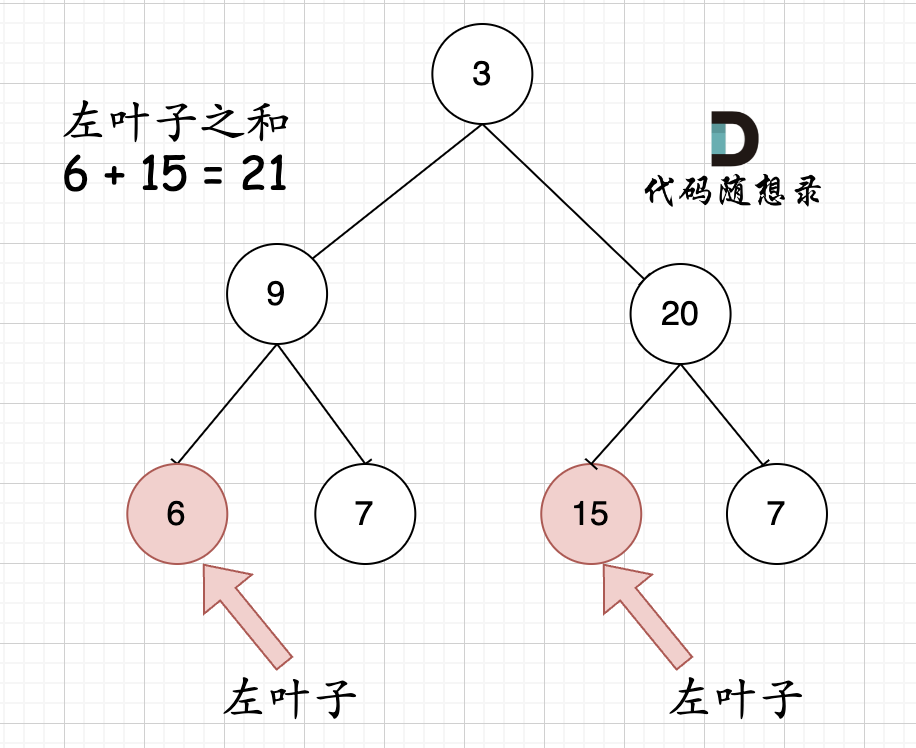
根据上图以及题目给的例子可知,我们无法直接判断当前节点是否为左叶子节点(因为无法将其与左侧节点区分)
所以需要通过当前节点的父节点来判断其左孩子是不是左叶子
即:如果某一节点的左子节点不为空,但该左子节点自身的左右节点为空,则找到一个左叶子节点
处理逻辑:
if(node->left != NULL && node->left->left == NULL && node->right->right == NULL){
//左叶子节点处理逻辑
}
本题仍然有递归和迭代两种解法
递归法
分析
三部曲
1、确定递归函数的参数和返回值
输入是根节点(每次的输入节点即为本次递归的根节点),返回值是左叶子节点之和,即int
2、确定终止条件
终止条件有两个,因为这里输入递归函数的“根节点”其实就是当前节点
如果当前节点为空,那么终止
如果当前节点以及是做叶子节点,那么也应该终止
if(root == NULL) return 0;
if(root->left == NULL &&root->right == NULL) return 0;
3、确定单层处理逻辑(即当前递归层的处理逻辑)
使用后序遍历的方式通过递归不断遍历左右子节点,并寻找左右子节点下的左叶子节点
如果遇到的话,就获取该节点的val,然后在每层递归返回值的时候累加左右子节点下的左叶子节点的值之和
//定义变量,存放左子节点的左叶子节点的值之和
int leftSum = sumOfLeftLeaves(root->left);//左
//找到左叶子节点
if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){
leftSum = root->left->val;
}
//以上两行代码对应过程是”使用父节点来判断其左孩子是不是左叶子节点“
int rightSum = sumOfLeftLeaves(root->right);//右
int sum = leftSum + rightSum;//中
return sum;
一定要明确左叶子节点的概念
虽然我们也遍历右节点,但是是为了寻找右节点下是否有左子节点,该子节点下又是否进一步存在左叶子节点
所以当遍历到某个右节点,那之后的递归操作一定会持续到触发leftSum为止(即在该右节点的子节点中找到叶子节点)
代码
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
//确定终止条件
if(root == NULL) return 0;
if(root->left == NULL && root->right == NULL) return 0;
//确定单层处理逻辑
//后序遍历
//定义变量,存放左子节点的左叶子节点的值之和
int leftSum = sumOfLeftLeaves(root->left);//左
//找到左叶子节点
if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){
leftSum = root->left->val;
}
//以上两行代码对应过程是”使用父节点来判断其左孩子是不是左叶子节点“
int rightSum = sumOfLeftLeaves(root->right);//右
int sum = leftSum + rightSum;//中
return sum;
}
};
注意
TBD
迭代法
分析
使用前中后序遍历都可以,具体操作和使用栈进行迭代法遍历一致
代码
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
//创建一个栈
stack<TreeNode*> st;
//判断根节点
if (root != NULL) st.push(root);
//定义结果变量
int res = 0;
while(!st.empty()){
//取出栈顶节点
TreeNode* node = st.top();
//弹出
st.pop();
//判断左叶子节点
if(node->left != NULL && node->left->left == NULL && node->left->right == NULL){
res += node->left->val;
}
//遍历左右子节点,压栈
if (node->left) st.push(node->left);
if (node->right) st.push(node->right);
}
return res;
}
};
注意
使用栈进行迭代法的前后序遍历时,要与层序遍历区分清楚
在while中,迭代法前后序遍历不需要记录当前栈的长度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号