【LeetCode二叉树#06】获取二叉树的所有路径(分析递归中的回溯机制)
二叉树所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

思路
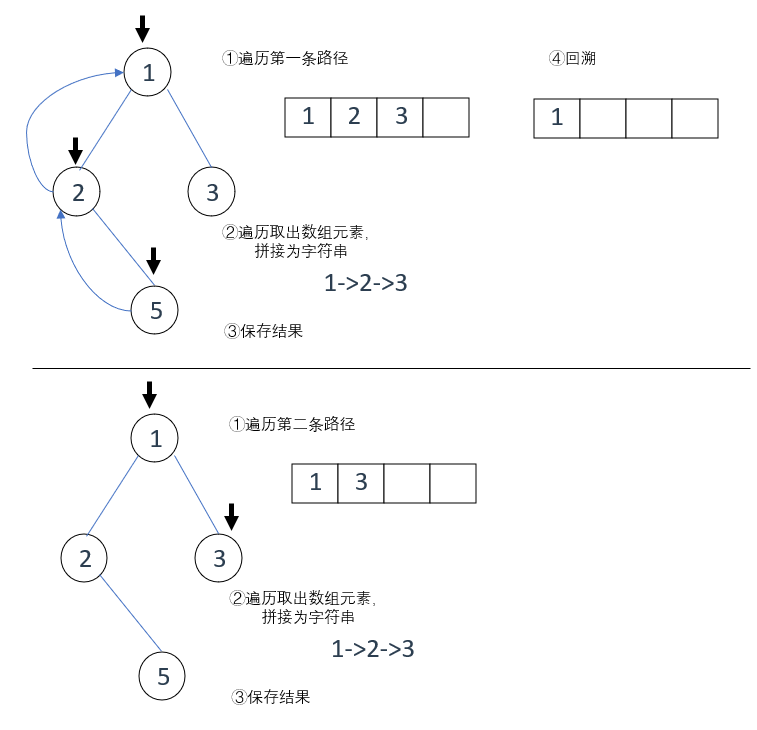
根据题意,每次遍历至子节点,我们都需要返回根节点然后从另外一条路径继续遍历
关键点是:返回,实现这个机制需要使用递归与回溯
且最后输出结果的顺序是根节点->子节点->叶子节点,也就是从上到下的顺序,因此可以使用前序遍历
代码
先写递归逻辑,还是递归的三部曲
1、确定递归函数的参数、返回值
需要传入的是根节点,然后记录每一条路径path,并保存至结果数组res;
不涉及返回值
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
}
在记录路径时,一开始我们是通过递归不断保存路径上每个节点的值,因此需要使用数组来保存
之后按照题目要求,输出时需要将一段路径用"->"连接,因此结果数组中保存的应该是字符串类型的路径
2、确定终止条件
由题意可知,从根节点到叶子节点才算构成一条完整路径
那么我们的终止条件可以设置为:当前节点是否为叶子节点
即
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
if(node->left == NULL && node->right == NULL){//左右子节点均为空时
//终止时的处理代码
}
}
因为使用vector来存放路径,所以在结束一条路径的遍历时,我们需要将path数组的值遍历出来,转换为string并拼接箭头
最后存放至res结果数组中。
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
if(node->left == NULL && node->right == NULL){//左右子节点均为空时
//终止时的处理代码
//定义一个string变量存放路径字符串
string spath;
//遍历path数组
for(int i = 0; i < path.size() - 1; ++i){
spath += to_string(path[i]);//将元素转换为字符串类型
spath += "->";//拼接箭头
}
//单独把最后一个节点(叶子节点)接上,因为其后不需要接箭头,所以不放在循环里
spath += to_string(path[path.size() - 1]);
//保存一条路径至结果数组
res.push_back(spath);
return;//结束
}
}
3、确定单层处理逻辑
这里的遍历逻辑是前序遍历,中左右
按理来说,“中”(处理中间节点)应该和“左右”一块放在终止条件后面
但是,这里情况比较特殊,中间节点就是我们需要记录的路径节点,因此需要先将其放入path中,即
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
path.push_back(cur->val);//将当前节点值放入path
if(node->left == NULL && node->right == NULL){//左右子节点均为空时
...
}
}
然后,左右的遍历处理与往常一样,不过得先判断左右子节点是否存在
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
path.push_back(cur->val);//将当前节点值放入path
if(node->left == NULL && node->right == NULL){//左右子节点均为空时
//终止时的处理代码
//定义一个string变量存放路径字符串
string spath;
//遍历path数组
for(int i = 0; i < path.size() - 1; ++i){
spath += to_string(path[i]);//将元素转换为字符串类型
spath += "->";//拼接箭头
}
//单独把最后一个节点(叶子节点)接上,因为其后不需要接箭头,所以不放在循环里
spath += to_string(path[path.size() - 1]);
//保存一条路径至结果数组
res.push_back(spath);
return;//结束
}
if(node->left != NULL){
traversal(node->left, path, res);
}
if(node->right != NULL){
traversal(node->right, path, res);
}
}
然后,重要的点来了
前面我们在梳理思路的时候分析了,当找到叶子节点后,我们就在path数组中记录了一条完整路径
那么此时我们需要将记录的节点“弹出”,直到只剩下根节点,然后再去寻找系下一条路径
上述过程即为 回溯
如何实现回溯呢?我们在前序遍历中遍历左右子节点时使用了 递归 ,那么当递归一层一层的执行,最后我们会找到某个叶子节点
此时按照递归的逻辑,最内层的递归会将获取到的结果层层返回
因为我们在最里层递归中已经将完整路径字符串保存到结果数组,所以我们可以利用递归返回值的过程,将每层递归记录的路径节点逐个pop掉
最后只剩下根节点,然后开始下一条路径的遍历
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
path.push_back(node->val);//将当前节点值放入path
//左右子节点均为空时找到叶子节点
if(node->left == NULL && node->right == NULL){//已终止递归,开始保存记录的路径节点
//终止时的处理代码
//定义一个string变量存放路径字符串
string spath;
//遍历path数组
for(int i = 0; i < path.size() - 1; ++i){//减一是因为最后一个节点需要在循环外处理
spath += to_string(path[i]);//将元素转换为字符串类型
spath += "->";//拼接箭头
}
//单独把最后一个节点(叶子节点)接上,因为其后不需要接箭头,所以不放在循环里
spath += to_string(path[path.size() - 1]);
//保存一条路径至结果数组
res.push_back(spath);
return;//结束
}
if(node->left != NULL){
traversal(node->left, path, res);
res.pop_back();//在递归返回过程中(回溯)不断删除之前记录的路径节点
}
if(node->right != NULL){
traversal(node->right, path, res);
res.pop_back();
}
}
完整代码
class Solution {
public:
//创建递归函数
//确定递归函数的参数和返回值
void traversal(TreeNode* node, vector<int>& path, vector<string>& res){
path.push_back(node->val);//将当前节点的值放入path //中
//确定终止条件
//左右子节点均为空时找到叶子节点
if(node->left == NULL && node->right == NULL){//已终止递归,开始保存记录的路径节点
//定义变量保存路径字符串
string spath;
//遍历path取出记录的路径节点
for(int i = 0; i < path.size() - 1; ++i){//减一是因为最后一个节点需要在循环外处理
spath += to_string(path[i]);//将元素转换为字符串类型
spath += "->";//使用箭头拼接
}
//单独把最后一个节点(叶子节点)接上,因为其后不需要接箭头,所以不放在循环里
spath += to_string(path[path.size() - 1]);
//保存一条完整路径
res.push_back(spath);
return;
}
//确定单层处理逻辑
if(node->left){//左
traversal(node->left, path, res);
path.pop_back();//在递归返回过程中(回溯)不断删除之前记录的路径节点
}
if(node->right){//右
traversal(node->right, path, res);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> path;
vector<string> res;
traversal(root, path, res);
return res;
}
};
注意点:
1、真的,别忘了输入参数时以引用方式输入
2、一般在递归三部曲的第三步:确认当前递归层的处理逻辑中,都会再次调用递归函数


 浙公网安备 33010602011771号
浙公网安备 33010602011771号