【LeetCode二叉树#04】判断对称二叉树、相同的树、另一棵子树、树的子结构(二叉树相等判断)
对称二叉树
给定一个二叉树,检查它是否是镜像对称的。

思路
本题中,不能单纯去比较左右子节点的是否对称(都有值且不为空)
因为如果按上面那样做的话,到子节点后就肯定是不对称的(对于左半边而言),但整体上看可能还是对称的,仍然满足题意,由此就会出现错误
因此,我们需要比较的是当前左右节点下的外侧和内侧的节点是否对称,如图所示:
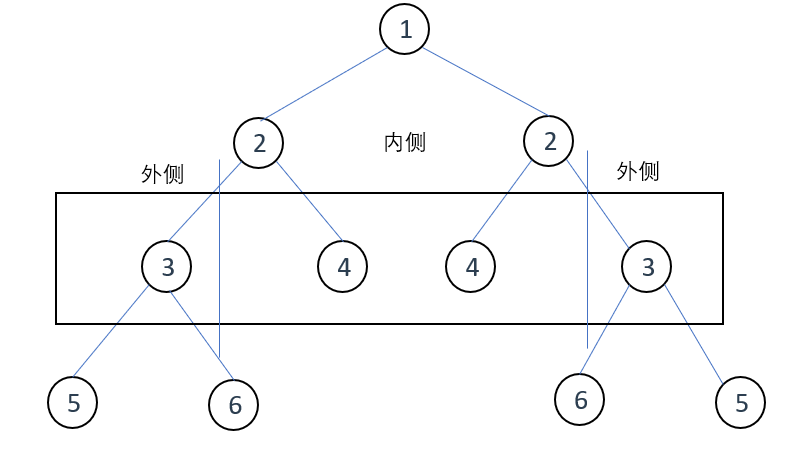
上图中,显然整课二叉树是对称的
我们在判断的时候只需将左2节点与右2节点的子节点按内侧与外侧区分,再进行比较即可
代码
递归法
按照递归三步走来:
1、确定递归函数的参数和返回类型
2、确定递归的终止条件
3、处理下一层的递归逻辑
class Solution {
public:
//确定递归函数的参数和返回值
bool cmp(TreeNode* left, TreeNode* right){
//确定终止条件
//四种情况
//空节点情况
//左节点为空,右节点不为空
if(left == NULL && right != NULL) return false;
//左节点不为空,右节点为空
else if(left != NULL && right == NULL) return false;
//左节点为空,右节点为空
else if(left == NULL && right == NULL) return true;
//非空但值不相等情况
//左右节点均不为空但值不相等
else if(left->val != right->val)return false;
//以下是左右节点均不为空且值相等的情况
//启用递归去判断他们的子节点(下一层)是否满足对称
//处理单层逻辑
bool outside = cmp(left->left, right->right);//外侧
bool inside = cmp(left->right, right->left);//内侧
bool res = outside && inside;
return res;//记得返回最终结果
}
bool isSymmetric(TreeNode* root) {
//判断根节点是否为空
if(root == NULL) return 0;
return cmp(root->left, root->right);
}
};
迭代法
定义两个节点,同时放入 队列 中,然后同时取出判断是否相等,直到遍历结束

class Solution {
public:
bool isSymmetric(TreeNode* root) {
//创建队列
queue<TreeNode*> que;
//判断根节点是否为空,为空直接对称
if (root == NULL) return true;
//获取左右节点(相对于root来说的)
//加入队列
que.push(root->left);
que.push(root->right);
//队列不为空则遍历
while(!que.empty()){
//取出队列中的两个节点
TreeNode* left = que.front();
que.pop();
TreeNode* right = que.front();
que.pop();
// //左节点为空,右节点有值//左节点有值,右节点为空//左右节点有值但不同
// if(left == NULL && right != NULL || left != NULL && right == NULL || left->val != right->val){
// return false;
// }else if(left == NULL && right == NULL){
// continue;
// }
//左右节点均为空
if(left == NULL && right == NULL){
continue;
}
//队列中如果没有同时放入两个节点就直接代表不对称了,即有一个为空就可以下判断
//其实还是对应之前的三种情况,只是在队列中表现方式不同
if((right == NULL || left == NULL|| (left->val != right->val))){
return false;
}
//排除上面的情况后就剩下不为空且对称的情况
//继续加入当前左右节点的子节点,依旧遵循内外侧原则
//外侧
que.push(left->left);
que.push(right->right);
//内侧
que.push(left->right);
que.push(right->left);
}
//完成上述遍历没返回false就是对称的
return true;
}
};
注意点
1、因为已经使用了队列,每次我们都需要放入两个节点,如果某次发现取的时候只有一个,那直接就可以判定当前情况为不对称‘
相同的树
https://leetcode.cn/problems/same-tree/
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
输入:p = [1,2,1], q = [1,1,2]
输出:false
思路
与对称二叉树的解法类似
只不过这里递归函数中,我们输入的分别是两个树的root
在处理单层逻辑时,要遵循以下原则:
二叉树A的左侧节点与二叉树B的左侧节点比较;
二叉树A的右侧节点与二叉树B的右侧节点比较;
上述结果完全相同才能证明两树相同
代码
使用递归法的思路
class Solution {
public:
//确定递归函数参数与返回值
bool cmp(TreeNode* p, TreeNode* q){
//确定终止条件(当前遍历节点为空)
if(p == NULL && q == NULL) return true;
else if(p == NULL || q == NULL)return false;
else if(p->val != q->val)return false;
//处理单层逻辑
bool leftside = cmp(p->left, q->left);
bool rightside = cmp(p->right, q->right);
bool res = leftside && rightside;
return res;
}
bool isSameTree(TreeNode* p, TreeNode* q) {
return cmp(q,p);
}
};
另一颗子树
https://leetcode.cn/problems/subtree-of-another-tree/
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
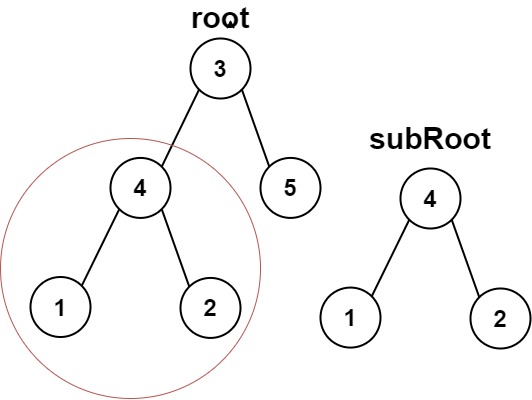
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:
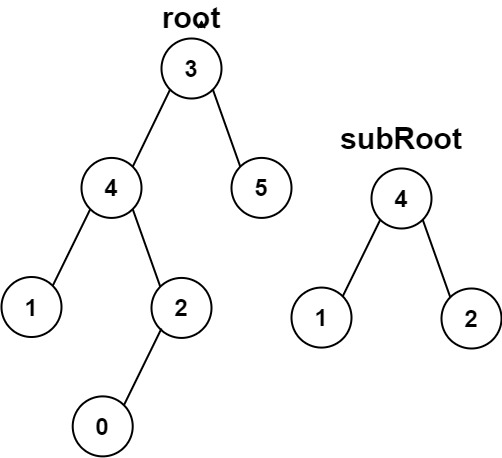
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104
思路
先读懂题目,题目要求我们在root中寻找一个与subRoot相等的子树,如果存在该子树返回true,否则返回false
那么会有以下几种情况:
1、root与subRoot直接就是相等的
- 两者都为NULL
- 两者满足相等条件
2、subRoot是root的左子树
3、subRoot是root的右子树
分别针对上述情况进行处理即可
两颗二叉树怎么才算相等?
两颗二叉树相等的定义是它们的结构相同且对应节点的值也相同。
具体来说,以下条件满足时,两颗二叉树才算相等:
- 两棵树的根节点的值相等。
- 递归比较两棵树的左子树和右子树是否相等。如果都相等,则这两棵树相等;如果至少有一棵子树不相等,则这两棵树不相等。
需要注意的是,如果一棵树的节点为空,而另一棵树对应节点不为空,则这两棵树不相等。
代码
主函数
一般来说,如果涉及递归操作,都应该先讲递归函数
但是这里有点特殊,我想先说一下主函数(不然会不清楚递归函数要达到的目的)
class Solution {
public:
//先得有一个用于判断相等数的函数
//确定递归函数参数与返回值
bool traversal(TreeNode* p, TreeNode* q){
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
//root不能为空
if(root == NULL) return false;
//root与subRoot相同,true
// if(traversal(root, subRoot))return true;
if(root->val == subRoot->val && traversal(root, subRoot)) return true;
//分别判断root的左边和右边有无与subRoot相同的,满足一边即可
// return isSameTree(root->left, subRoot) || isSameTree(root->right, subRoot);
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
};
在主函数isSubtree中,我们要判断的root中是否存在subRoot
首先得确定root的根节点不为空
然后判断当前节点(根节点)的值是否与subRoot当前节点的值相等【两棵树的根节点的值相等】
除此之外,还要判断root中是否存在与subRoot相等的子树【结构上相等】
判断结构的时候就需要使用递归函数遍历所有节点了,待会讲递归函数
如果在结构和数值上都相等,那么可以返回true
否则需要在再继续去root的左右子树中找与subRoot相等的子树
具体到操作上就是:递归调用主函数
是的,就是因为这个迷惑的操作,所以需要先说主函数逻辑。。。
在递归查找root左右子树时,只要有一边找到与subRoot相等的子树,主函数就可以返回true
递归函数
根据上述分析,整体代码中其实使用了两处递归
主函数递归负责在root中递归查找左右子树;
而traversal则负责在主函数递归中,判断当前root的子树是否与subRoot相等;
class Solution {
public:
//先得有一个用于判断相等数的函数
//确定递归函数参数与返回值
bool traversal(TreeNode* p, TreeNode* q){
//确定终止条件(当前遍历节点为空)
if(p == NULL && q == NULL) return true;//当前root子树和subRoot均为空的情况,相等
else if(p == NULL || q == NULL) return false;//当前root子树和subRoot一方为空的情况,不相等
else if(p->val != q->val) return false;//当前root子树和subRoot值不相等,不相等
//处理单层逻辑
//递归查找当前root子树的左子树
bool leftside = traversal(p->left, q->left);
//递归查找当前root子树的右子树
bool rightside = traversal(p->right, q->right);
//综合左右子树情况,均返回true则表示结构上相等,判定当前root子树和subRoot相等
bool res = leftside && rightside;
return res;
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
}
};
完整代码
class Solution {
public:
//先得有一个用于判断相等数的函数
//确定递归函数参数与返回值
bool traversal(TreeNode* p, TreeNode* q){
//确定终止条件(当前遍历节点为空)
if(p == NULL && q == NULL) return true;//当前root子树和subRoot均为空的情况,相等
else if(p == NULL || q == NULL) return false;//当前root子树和subRoot一方为空的情况,不相等
else if(p->val != q->val) return false;//当前root子树和subRoot值不相等,不相等
//处理单层逻辑
//递归查找当前root子树的左子树
bool leftside = traversal(p->left, q->left);
//递归查找当前root子树的右子树
bool rightside = traversal(p->right, q->right);
//综合左右子树情况,均返回true则表示结构上相等,判定当前root子树和subRoot相等
bool res = leftside && rightside;
return res;
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
//root不能为空
if(root == NULL) return false;
//root与subRoot相同,true
// if(traversal(root, subRoot))return true;
if(root->val == subRoot->val && traversal(root, subRoot)) return true;
//分别判断root的左边和右边有无与subRoot相同的,满足一边即可
// return isSameTree(root->left, subRoot) || isSameTree(root->right, subRoot);
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
};
树的子结构
https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof/
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000
思路
与上一题思路一致
代码
代码方面,递归函数的停止条件需要做一下变化
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
bool traversal(TreeNode* A, TreeNode* B){
//确定停止条件
if(B == NULL) return true;//当B遍历到了叶子节点,意味着B树是A树的子结构
//A、B同时为空表示没找到相同子结构,A先为空则表示B不可能为子结构,均返回false
if(A == NULL && B == NULL || A == NULL) return false;
if(A->val != B->val) return false;
// if(A == NULL || A->val != B->val) return false;//也可以这样判断
//确定单层处理逻辑
bool leftside = traversal(A->left, B->left);
bool rightside = traversal(A->right, B->right);
bool res = leftside && rightside;
return res;
}
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
if(A == NULL || B == NULL) return false;
if(A->val == B->val && traversal(A, B)) return true;//确保结构一致
return isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号