【LeetCode二叉树#00】二叉树的基础知识
基础知识
分类
满二叉树
如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。
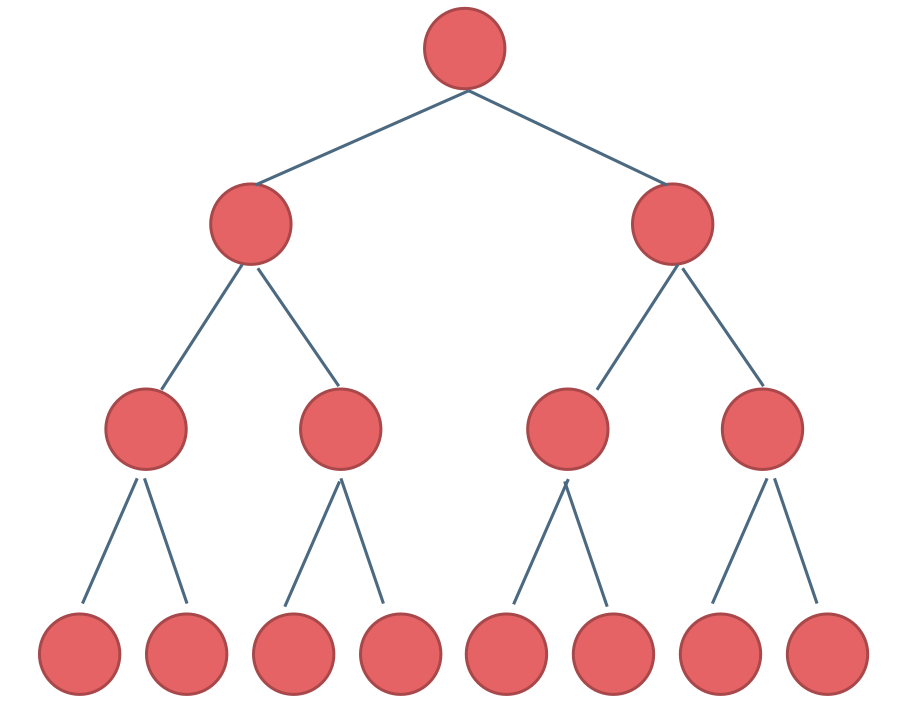
完全二叉树
除了底层外，其他部分是满的，且底层从左到右是连续的，称为完全二叉树
满二叉树一定是完全二叉树
举个例子：
完全二叉树
1
/ \
2 3
/ \ / \
4 5 6
不是完全二叉树
1
/ \
2 3
/ \ / \
4 5 6
二叉搜索树
例如：
6
/ \
3 9
/ \ / \
1 4 8 10
二叉搜索树里面的节点是有顺序的
左子树（左半边）的所有节点都小于中间节点
右子树（右半边）的所有节点都大于中间节点
并且在左/右子树的子树中也满足该规律
平衡二叉搜索树
左子树和右子树高度差的绝对值不能大于1
什么意思呢？例如:
0 6
/
1 3
/ \
2 1 4
上述二叉树不是平衡二叉搜索树
左子树的高度是2，右子树的高度是0，作差绝对值为2
再如：
0 6
/ \
1 3 9
/ \
2 1 4
这个就是平衡二叉搜索树
左子树的高度是2，右子树的高度是1，作差绝对值为1（右子树再加1个节点仍然还是）
又如：
0 6
/ \
1 3 9
/ \ /
2 1 4 8
/
3 0
这个还是平衡二叉搜索树
其左子树本身（从3开始往下的）满足条件，整棵树的左右子树也满足条件
C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。
平时在使用容器时要有意识去了解其底层实现是什么数据结构（这样才知道所使用的数据结构中的元素是否有序、时间复杂度是多少、为什么）
存储方式
链式存储
如图所示
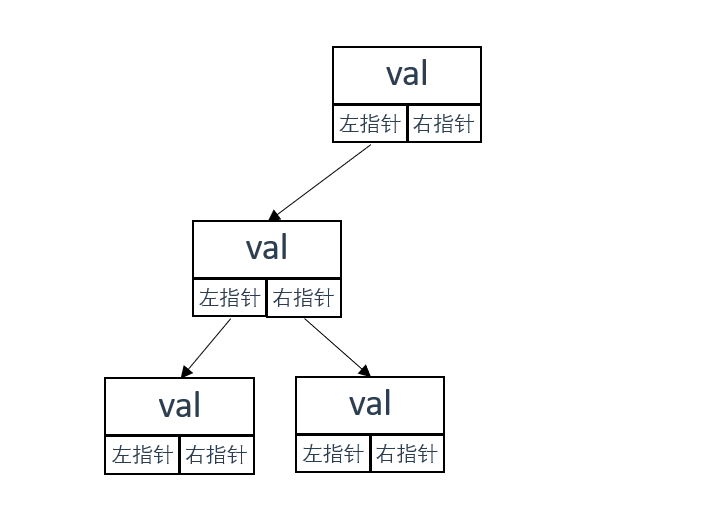
链式存储顾名思义就是使用指针（类似链表）的方式表示树
线性存储（了解）
其实就是用数组来存储二叉树，顺序存储的方式如图：
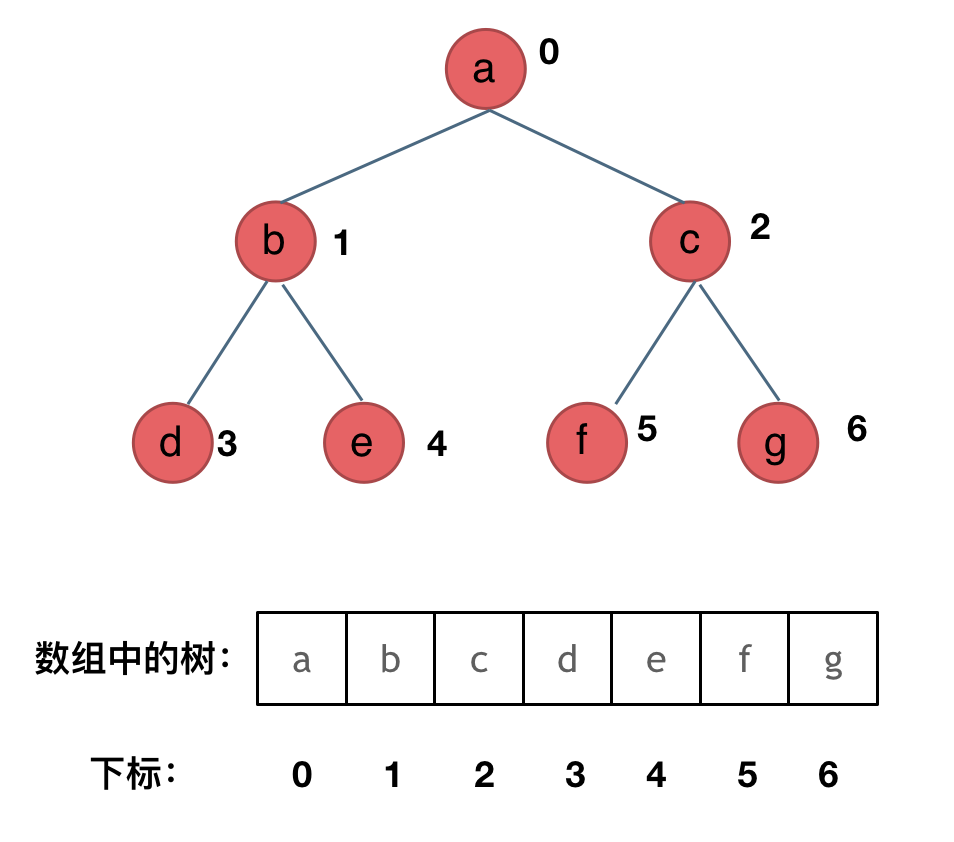
用数组来存储二叉树如何遍历的呢？
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。
但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。
所以大家要了解，用数组依然可以表示二叉树。
注意（构造二叉树）
LeetCode上在做题时，二叉树通常是封装好的
但是实际面试的时候，有可能要手写待传入的数据。比如：请传入一个二叉树
因此，需要掌握构造一个二叉树的方法
平时做题的时候我们通常使用链式存储老保存一个二叉树
其实说白了就是一个链表，只不过这个链表的节点上有两个指针，分别指向左右子节点
（那就是双向链表咯）
于是，我们可以构造一个双向链表来表示一颗二叉树，在传入二叉树时将该链表的头结点传入即可
二叉树遍历方式
二叉树的遍历方式实际上对应与图论中的两种遍历方式：深度优先搜索和广度优先搜索
深度优先搜索
一般用 递归 的方式实现
前序遍历、中序遍历以及后序遍历均数据深度优先搜索
描述一下就是：在选定一个节点后，一直沿一跳路径搜索到末尾，然后递归回到最开始的位置再换方向继续搜索
当然使用非递归的方式也可以实现，一般使用 迭代法（即采用 栈 去模拟递归）
理论上，用递归解决的遍历问题都可以用相对应的迭代法解决（只是有些可能会麻烦一些）
（实际上计算机在实现递归时，底层就是用的栈）
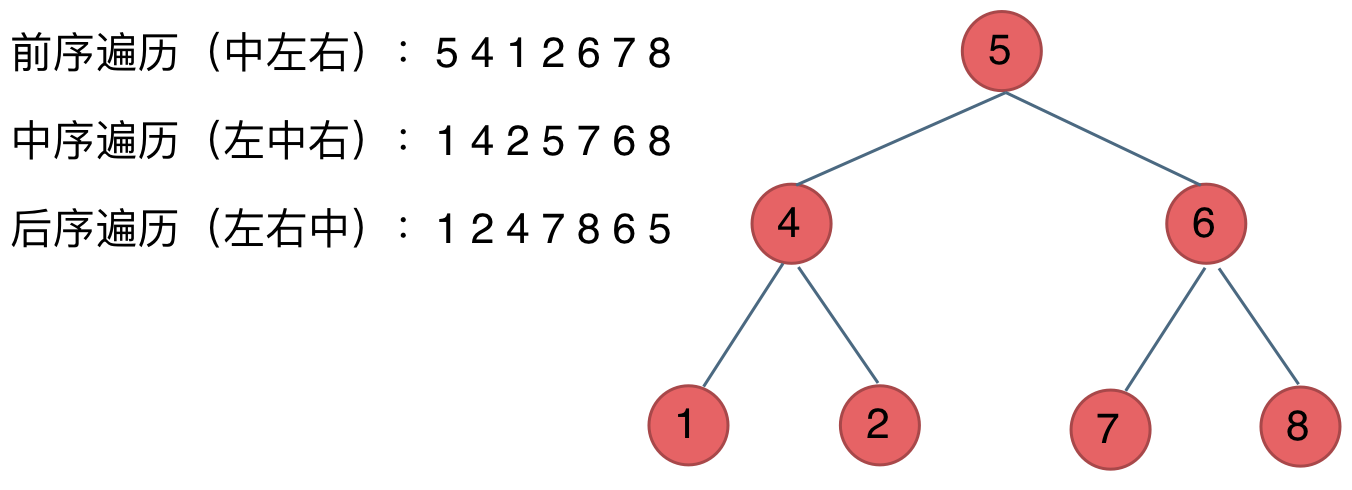
区分前/中/后序遍历
首先明确，这三种方式都是一条路先搜索到头再换方向的
那么他们的区别就是遍历时候的方向顺序
前序：中左右
中序：左中右
后序：左右中
其实“前中后”描述的就是"中"的位置
例如：
广度优先搜索
通常指一层一层遍历二叉树的方式（在图论中是一圈一圈的遍历）
常见方法是：层序遍历
一般使用 队列 实现
二叉树定义方式
顺序存储就是用数组来存，这个定义没啥可说的，我们来看看链式存储的二叉树节点的定义方式。
C++代码如下：
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
二叉树的定义 和链表是差不多的，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右子节点。
**在现场面试的时候 面试官可能要求手写代码，所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。
