【LeetCode字符串#05】基于个人理解的KMP算法图解,以及应用到strStr()函数实现
KMP算法(用于实现 strStr())
strStr()函数是用来在一个字符串中搜索是否存在另一个字符串的函数,其匹配字符串方式为KMP算法
KMP算法基础理论
假设有如下两个字符串
文本串 aabaabaaf
模式串 aabaaf
我们希望在文本串中匹配出模式串
Intro
暴力法
使用两层for循环逐个匹配,当匹配不上时,模式串整体后移一位,继续逐个匹配

从代码实现的复杂度来看,这种做法最坏的情况复杂度是O(m*n),即:文本串长度 * 模式串长度
下面来看看KMP是怎么做的
KMP
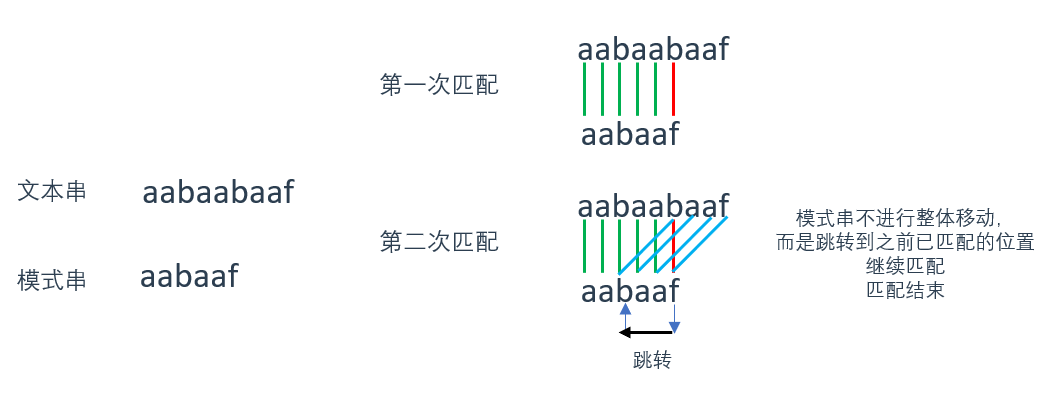
使用KMP算法,当遇到不匹配值 f 时,当前指针会跳转到 b 处继续匹配
看到这里肯定有疑问:为什么知道要跳转到 b 处继续匹配?
因为KMP算法中使用到了 前缀表
前缀表
上面的讨论中
"当出现不匹配的值跳转到b处继续匹配"
这件事情用具体的理论来表述是:
当出现不匹配值 f 时,f 的前面的子串是 aabaa ,该子串的后缀是 aa
根据KMP算法,我们要找到子串 aabaa 前缀与后缀相同的位置
显然这个位置就是 b 所在之处,因此从这里开始继续匹配
也就是说:"当出现不匹配值时,我们要看不匹配值前面的子串,找出该子串最长相等前后缀是多少"
下面对以上出现的新名词做解释
什么是前/后缀?
举个例子
aabaaf
|___|
即:
a
aa
aab
aaba
aabaa
如上面,前缀是包含首字母,不包含尾字母的所有子串
aabaaf
|___|
即:
f
af
aaf
baaf
abaaf
而后缀是只包含尾字母,不包含首字母的所有子串
如何求最长相等前后缀?
以aabaaf为例
aabaaf
a 0(理论上a没有前后缀,所以为0)
aa 1(前缀a,后缀a,因此是1)
aab 0(a、b不等,为0)
aaba 1
aabaa 2
aabaaf 0
前缀表在哪?
这里得到了一个序列(从上到下):[0, 1, 0, 1, 2, 0]
那么这个就是所谓的前缀表
使用前缀表
根据上面的讨论,我们得到了模式串的前缀表
aabaaf
010120
那么如何使用前缀表进行匹配?

我们在子串 aabaa 的 后缀aa 的后面遇到了不匹配值,那么我们就要从子串 aabaa 的 前缀aa 的后面(b处)继续往后匹配。
说白了就是:
子串aabaa(不匹配值前面的子串)它的最长相等前后缀的长度就是我们要继续匹配的位置
最长相等前后缀在前缀表中记录为2,那么我们就要跳到字符串中2的位置
012345
aabaaf
010120
↑
也就是b的位置(即,前缀的后面)
这里用于存放前缀表的数组一般称为next数组,如何去求,后面再说
KMP算法实现
前缀表的实现需要依赖next数组,因此我们需要构建它
构造next数组
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
初始化
定义两个指针 i 和 j ,j 指向前缀末尾位置(不匹配值的前一个位置),i 指向后缀末尾位置。
从判断前后缀是否相同的角度解释
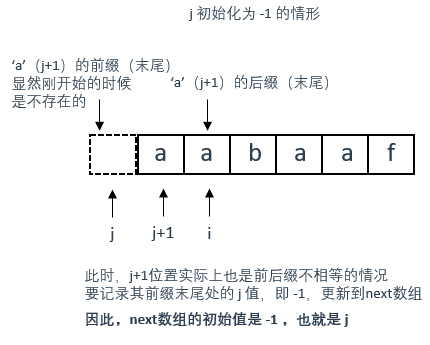
从初始化的角度解释
初始化值如下:
int j = -1;
next[0] = j;
其实 j 也不一定初始化为 - 1
例如之前的前后缀示例中,我们的初始化值为0
这里是为了让next数组中的元素统一为:0,-1,1,才将 j 初始化为 -1 的
next[i] 表示 i(包括i)之前最长相等的前后缀长度(详见上面的解释,其实就是 j )
同理,next[j+1]表示 j+1(包括j+1)之前最长相等的前后缀长度
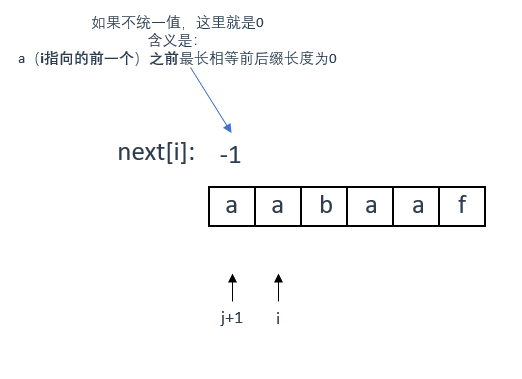
详见之前的求最长相等前后缀示例,对照来看
规定好指针的定义后,现在要开始遍历判断前后缀的情况了
判断前后缀是否相同(j初始化为-1)
这里我先画一个图来模拟整个过程
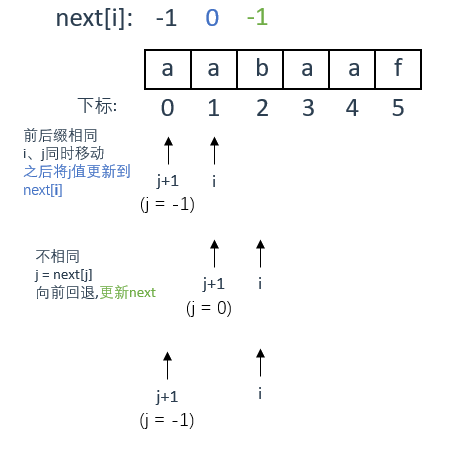
刚开始的时候,j+1指向 a ,i 指向 a
前后缀相等
此时 s[j+1] = s[i] ,前后缀相等。
故两个指针同时后移一位(但具体过程是 j 先 ++,然后再到for循环的 i++),更新 j 的值到next[i](注意是i)
代码如下:
//如果找到匹配值,j++(也就是把j+1往后移),并保存匹配值的位置(j值)到next数组
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j;
要明确一点: next数组(前缀表的具体实现)用来寻找前后缀相等时 j (指向前缀末尾位置)的位置 ,其存放的是
图示角度解释
因为这里 j 初始化为-1,所以从图中来看,next保存的是当前位置(j+1指向)的前一个位置,这也和前缀的定义是相符的,即不包含j+1指向位置的元素
(实在不理解就当成是初始化就行,j+1指向的'a'前面没有子串,也就没有前缀,所以给个初始值-1)
代码角度解释
虽然当满足 s[j+1] = s[i] 时,立刻进行 j++,但此时外层for循环并没有结束,我们仍可以通过 i 找到 j++之前的 j 值指向的位置,并将当前更新后 j 值保存到 next数组中(对应图示中的行为)
注意,这里next数组中存的是 j 的值,不是 j+1的值
j 值才是前缀末尾位置,而 j+1只是遍历当前模式串使用的一个指针
通过next数组我们可以找到最近一次满足 s[j+1] = s[i] 条件时,指针j+1的位置
前后缀不相等
第二轮,j+1指向 a ,i 指向 b

此时 s[j+1] != s[i] ,前后缀不相等,那么指针 j+1要向前回退
怎么回退呢?根据之前理论部分的讨论,遇到不匹配的值,要看当前 j+1 的前一位在next数组中对应的值,使用该值作为回退的依据,对应到图中就是让 j 等于next中当前位置(j+1指向的)前一位的值(也就是next[j])
简单来说,就是从next数组中找到上次前后缀相等时指针 j+1指向的位置
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
注意这里是要循环去回退,因为可能要回退多次,所以不能用 if
并且还要注意加上条件,判断是否已经退到头了(j >= 0)
代码构造next数组的逻辑流程动画如下:

整体代码:
void getNext(int* next, const string& s){
//初始化j和next数组
int j = -1;
next[0] = j;
//开始遍历模式串
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
//如果没找到匹配值,使用next数组回退
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 不断地从next数组中找上次前后缀相等时指针 j+1指向的位置
}
//如果找到匹配值,j++(也就是把j+1往后移),并保存匹配值的位置(j值)到next数组
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}
总结
实际上这样捋一遍可能还是有点乱,我认为原因之一是初始化的问题
即:为了将 next数组中的值统一成[-1,0,1]这三种,在初始化时将 j 初始化为-1
但是只要记住一下几点应该还是能够想明白的:
1、两个指针 i 和 j 的定义
j 指向的是前缀末尾位置(不匹配值的前一个位置)
i 指向的是后缀末尾位置
2、遵循"循环不变量"原则
在KMP算法中,循环不变量指的是:每当我们遇到不匹配的值时,总是去找其前一个值所在位置下标在next数组中对应的记录值,然后由此回退到上次前后缀相等(s[i] == s[j + 1])的位置
3、next数组存的是什么
next数组存放的是最后一次前后缀相等的位置
实现 strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1: 输入: haystack = "hello", needle = "ll" 输出: 2
示例 2: 输入: haystack = "aaaaa", needle = "bba" 输出: -1
说明: 当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。 对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
思路
利用上面介绍的KMP算法
先求出needle 字符串(即 模式串)的next数组
然后还是用双指针去遍历haystack 字符串(即 文本串)和needle 字符串
如果值匹配,两个指针同时向后移动,不匹配则通过next数组返回上次匹配的位置,继续比较
步骤如下:
1、实现getNext函数用于计算模式串前缀表
2、创建一个数组作为next数组(长度与模式串相等)
3、定义指针 j (规则要与计算next数组是保持一致,之前是-1,这里也要是-1)
4、从0开始遍历文本串
- 不匹配的就去next里找位置回退
- 匹配的,令 j 和 i 指针继续往下走(j后移就相当于j+1后移)
5、当 j 来到模式串的末尾,搜索结束,此时需要返回
- 文本串指针i遍历到的当前位置减去模式串的长度(从0开始数的)再加1就可以得到文本串中出现模式串第一个字符的位置
代码
明确两个指针分别遍历的是谁
j 指针负责模式串;
i 指针负责文本串;
class Solution {
public:
//先定义计算next数组的函数
void getNext(int* next, string& s){
//初始化j和next数组
int j = -1;
next[0] = j;
//开始遍历模式串
for(int i = 1; i < s.size(); ++i){//注意i从1开始
//如果没找到匹配值,使用next数组回退
while(j >= 0 && s[j + 1] != s[i]){
j = next[j];//不断地从next数组中找上次前后缀相等时指针 j+1指向的位置
}
//如果找到匹配值,j++(也就是把j+1往后移),并保存匹配值的位置(j值)到next数组
if(s[j + 1] == s[i]){
j++;
}
next[i] = j;//因为j已经++,利用i来把更新后的j值存到++之前下标对应的next中的位置
}
}
//使用next函数计算needle的前缀表
int strStr(string haystack, string needle) {
//判断needle是否为空
if(needle.size() == 0){
return 0;
}
//定义一个数组作为next数组,长度与模式串相等
int next[needle.size()];
//计算needle的next数组
getNext(next, needle);
//定义指针j,因为我们计算next数组时j初始化为-1,这里也保持一致
int j = -1;
//开始遍历文本串
for(int i = 0; i < haystack.size(); ++i){
//判断是否匹配的代码与getNext中一致
while(j >= 0 && haystack[i] != needle[j + 1]){//不匹配时,从next数组找回退位置
j = next[j];
}
if(haystack[i] == needle[j + 1]){//匹配,i、j同时后移
j++;
}
//判断一下是否匹配结束
//因为j是用来遍历模式串的,如果j到达模式串尾部,那么说明文本串中出现了模式串,结束
if(j == needle.size() - 1){
//用文本串指针i遍历到的当前位置减去模式串的长度(从0开始数的)再加1就可以得到文本串中出现模式串第一个字符的位置
return (i - needle.size() + 1);
}
}
return -1;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号