【LeetCode链表#11】环形链表II(双指针)
环形链表II
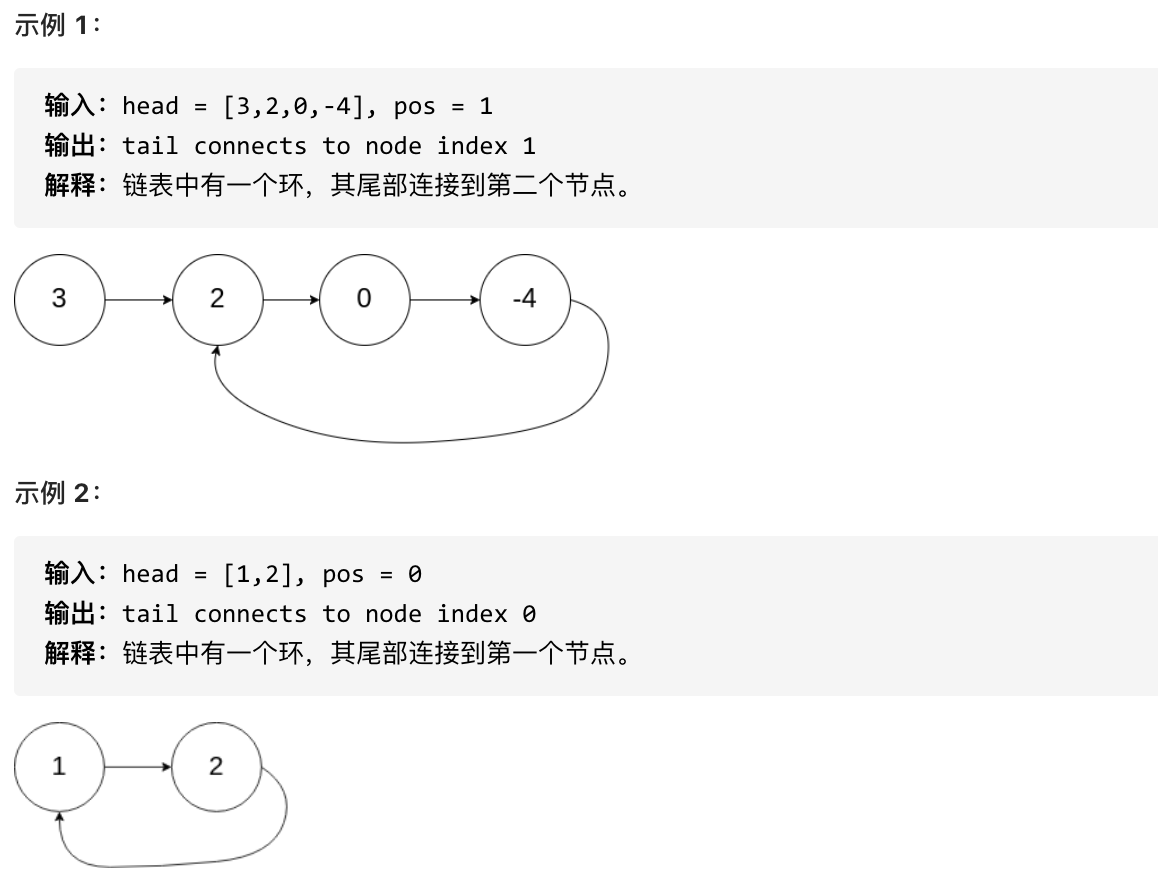
题意: 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
思路
首先,要明确题目需要什么
"给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null"
我们要做的不仅是判断链表是否有环,而是要返回链表开始入环的第一个节点
也就是链表环的起始位置(如示例1中的节点2)
那么解决问题的过程就分为两部分:判断是否存在环和找到环的入口
判断环(双指针法)
可行性解释
判断是否存在环结构可以使用快慢指针实现
想象一下,如果链表中没有环,那么走在前面的快指针是不可能与慢指针相遇的(追不上)
反之,如果存在环结构,那么快指针在进入环结构之后会在环内不断循环,此时慢指针经过一段时间后也会进入环结构,最终被快指针追上,两者相遇,从而证明环的存在。
因此,快慢指针判断环是可行的。
快慢指针如何定义?
在说明可行性时,我们没有具体给出快慢指针要怎么定义
设定:快指针每次移动两个节点,慢指针每次移动一个节点
为什么?
还是像之前说的,一定是快指针先进入环
当慢指针也进入环之后,就形成了快指针追慢指针这样一个情况
此时由于我们的设定,快指针相对于慢指针的移动速度是一个节点
也就是说,在环内,快指针以每次移动一个节点的速度去接近慢指针
因此最终快慢指针一定会相遇

上述过程也解释了为什么不能把快指针的速度设置为3,因为这样两个指针在环内的相对移动速度就会变成2,快指针就有可能跳过慢指针导致两者不能相遇。
找到环的入口
设置变量
现在可以开始找环结构的入口
注意:这个才是题目的要求,而不是要你直接返回快慢指针在环内相遇时的位置
从快慢指针相遇这个时间节点开始分析,我们可以设出几个变量
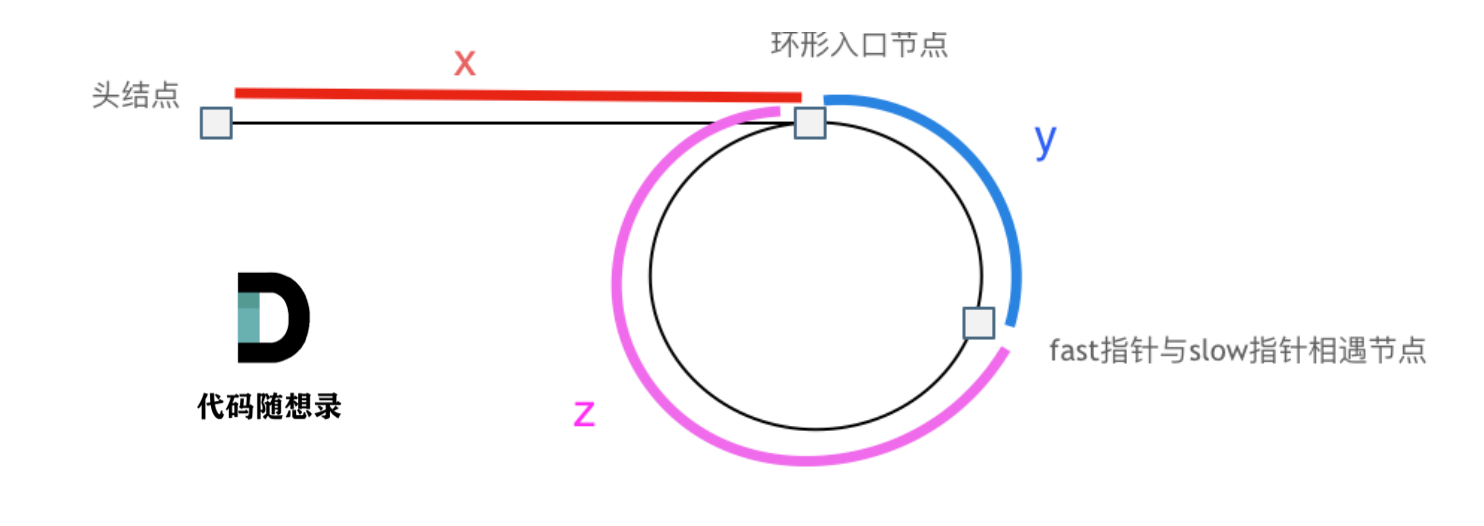
设:
从头结点到环形入口节点的节点数为x;
环形入口节点到fast指针与slow指针相遇节点节点数为y;
从相遇节点再到环形入口节点节点数为z;
一些推导
可以用这些变量来描述快慢指针的行为:
快指针至少走过了x+y个节点,并且在环内转了 n 圈,即:
$$
fast = x+y+n(y+z)
$$
而慢指针从头节点开始到进入环并被快指针追上,经过的节点数就是x+y,即:
$$
slow=x+y
$$
因为快慢指针的移动速度是 2:1 ,因此可以得到以下等式:
$$
fast=2slow
$$
$$
x+y+n(y+z) = 2(x+y)
$$
经过化简可以得到:
$$
n(y+z) = x+y
$$
$$
x = n(y+z) - y
$$
在上述式子中,单看x和-y是没有什么关系的
因此,人为调整公式里的圈数n将负数转化掉来寻找规律(快指针在环内转几圈都是无所谓的,因此n是几可以按需调整)
$$
x = (n-1)(y+z)+ (y+z)- y
$$
$$
x = (n-1)(y+z)+z
$$
快指针在环内至少转一圈以后才会与慢指针相遇(快指针要在环里等慢指针,想想)
因此,n>=1
当 n=1 时,可以得到
$$
x = z
$$
结论
上面的推导只是为了得出寻找入口的方法
最后的结果非常关键,x = z 说明了:当快慢指针在环内相遇后,此时分别在相遇点和头节点处各设一个指针,那么这两个指针一定会在环的入口处相遇
由此我们便可以找到环的入口
n不等于1时成不成立呢?也是成立的
因为 n 代表的是快指针在环内经过的圈数,经过1圈在入口处相遇和经过10圈在入口处相遇没有区别,相遇的位置永远是要找的入口。(关键是 z 字段距离是多少)
代码
代码实现也是分为两部分
先使用快慢指针找到环结构,然后定义新的两个指针去找到环入口
public class Solution {
public ListNode detectCycle(ListNode head) {
//定义快慢指针
ListNode fast = head;
ListNode slow = head;
//快指针只要没指向空就不断往后走
while(fast != null && fast.next != null){//fast一次跳两步,因此还需要判断next
fast = fast.next.next;
slow = slow.next;
//如果找到环
if(fast == slow){
//定义两个新的指针用来找入口
ListNode crossIndex = fast;//等于slow也行,现在这俩一样
ListNode headIndex = head;//位于头节点的新节点
while(headIndex != crossIndex){
crossIndex = crossIndex.next;
headIndex = headIndex.next;
}
return crossIndex;//return谁都可以,这俩也一样现在
}
}
return null;
}
}
c++版
步骤:
1、定义两个指针(快慢指针)指向头节点
2、while循环遍历链表,快指针一次走两步,慢指针一次走一步
3、当快慢指针相遇(相等),定义两个新指针,一个指向头节点,一个指向当前相遇位置
4、使用while不断遍历这两个指针,直到它们相遇,返回当前指针位置(返回谁都可以)
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;//定义快慢指针
ListNode* slow = head;
//遍历链表,fast每次走两格,slow每次走一格
while(fast != nullptr && fast->next != nullptr){//快指针一次走两步,因此还需要判断其下一步是否为空
fast = fast->next->next;
slow = slow->next;
//如果找到环,设定两个新指针
if(fast == slow){//在头节点和此处分别定义两个新指针
ListNode* crossIndex = fast;//slow也行
ListNode* headIndex = head;
while(crossIndex != headIndex){
crossIndex = crossIndex->next;
headIndex = headIndex->next;
}
return crossIndex;
}
}
return NULL;
}
};
二刷问题
1、fast设置问题
fast和slow初始时都应该指向head,区别是遍历过程中,fast每次走两步(fast = fast->next->next;),而slow每次只走一步。
因此,在第一部分寻找环结构时,while遍历的结束条件应该是:fast遇到空时结束(与slow无关),且因为fast一次走两步,所以还需要判断fast的下一个节点是否为空
2、公式推导
如果要推导公式的话,先把三个点有环的情况画出来,设置x、y、z,然后写公式,下面我把公式总结一下
fast = x+y+n(y+z);
slow = x+y;//这个容易忘,需要特别记一下
fast = 2*slow;
x+y+n(y+z) = 2*(x+y);
x+y = n(y+z);
x = (n-1)y+nz;
= (n-1)(y+z)+z;
根据分析,快指针至少需要在环内走一圈才会遇上慢指针,因此n是大于等于1的,当n = 1时,得到解题需要的结论,即x = z;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号