【算法day4】堆结构、堆排序、比较器以及桶排
堆与堆结构(优先级队列结构)
知识点:
- 堆结构就是用数组实现的完全二叉树结构
- 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
- 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
- 堆结构的heaplnsert与heapify操作
- 堆结构的增大和减少
- 优先级队列结构,就是堆结构
一段连续的数组是可以想象成完全二叉树结构的
例如
[3,5,2,7,1,9,6]
[0,1,2,3,4,5,6]
对应到完全二叉树结构中得到
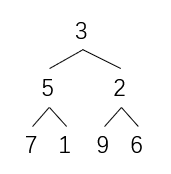
连续的一段数组可以用一个"size"描述,表示一个连续的数组到达的位置(与数组长度无关)
这个例子中的size = 7
若用数组下标表示该完全二叉树,则
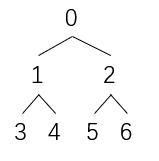
那么生成树的对应规则是:
i位置(0~6)对应的左分支为:2*i+1
例如,
0的左分支是2*0+1=1;
1的左分支是2* 1+1=1,2的左分支是2*2+1=5;
3的没有左分支,因为按照公式计算后所得超过了size,456同理
i位置(0~6)对应的右分支为:2*i+2
i位置(0~6)对应的父分支为:(i-1)/2
例如,
5位置的父分支节点是(5-1)/2=2,6位置的父分支节点是(6-1)/2=2.5,取整为2
大/小根堆
定义:在完全二叉树中,每一棵子树的最大值就是头节点的值
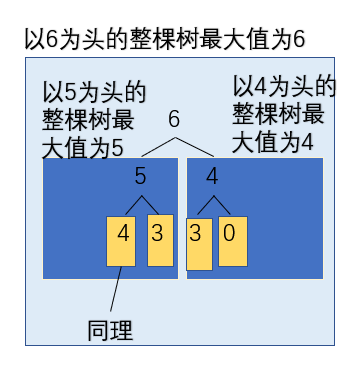
反之,则为小根堆
将连续数组表示为堆(heapinsert,将大数往上移)
假设,现在有一个数组[],设一个变量为heapsize = 0

heapsize = 0意味着数组中从0出发的连续的0个数现在构成一个堆
此时,用户给了一个数,假设是5
那么根据heapsize的指示,5被放在0位置上,heapsize+1 = 1
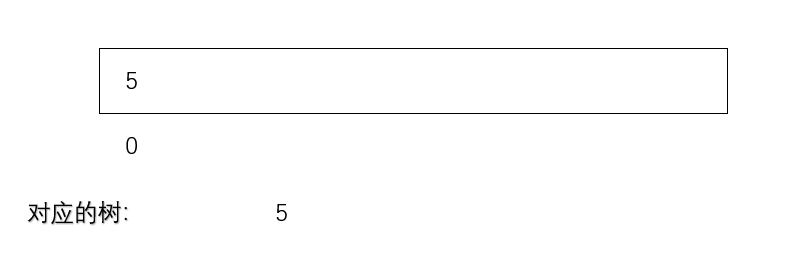
用户又给了一个数3,根据heapsize的指示,3被放在1位置上,heapsize+1 = 2

用户再给一个数6,根据heapsize的指示,6被放在2位置上,heapsize+1 = 3
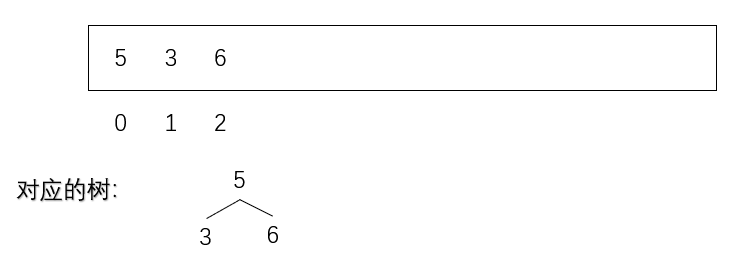
此时的树不满足“大根堆”要求,于是6就需要和自己的父去做比较
6的位置是已知的(heapsize还没变)
根据生成树的规则可以找到6的父值
父分支=(i-1)/2=(2-1)/2=0.5,取整为0
于是6需要与0位置的数(也就是5)比较大小
6比5大,于是两者交换位置,树又满足大根堆的要求了
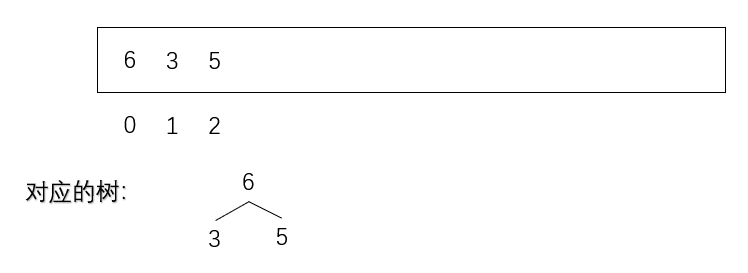
如果再进来一个更大的数也是同样的操作
规律就是,新来的数一直与自己的父值比较,若大于父值则交换,直到比较完所有的父值或者来到整棵树的头部就停止。
若小于就不动。
这样操作后可以保证用户给的每一个数到了数组里,形成的结构均为大根堆
heapify
在现有的堆中插入一个数,该数较小不符合当前位置,为了整体结构仍满足大根堆,要将其往下移,该操作称为heapify,代码实现如下

堆排序
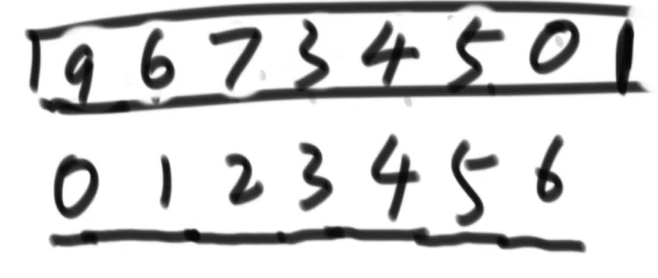
假设有数组
[3,5,9,4,6,7,0]
[0,1,2,3,4,5,6], heapsize = 0
现在按照之前的方法从0位置到6位置让该数组排成大根堆
排完之后结果如下
数组变为由大到小的排序
对应的树结构是,当前heapsize = 7
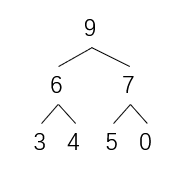
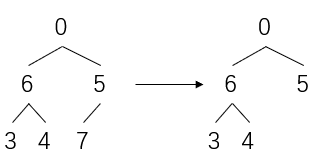
此时,将0位置的最大值与6位置的最小值交换
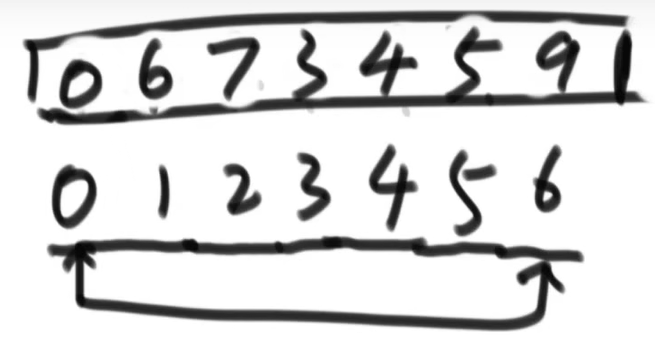
heapsize -- = 6
这样做的目的是让最大值来到堆的末尾,然后让最大值与堆断开联系(因为它是已经排好的数,堆没必要再包含它)
那么当前的树结构变为
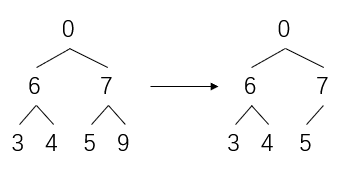
舍弃堆末尾的最大值9
然后让剩下的数继续做heapify,把0再弄到堆的末尾
排完之后结果如下

树结构
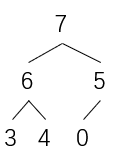
此时,又将0位置的最大值与5位置的最小值交换
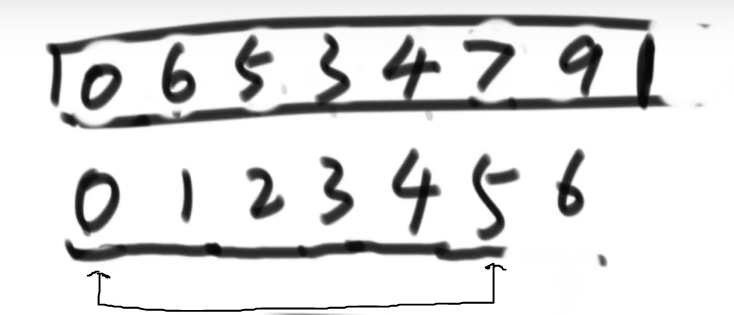
heapsize -- = 5
当前的树结构变为
舍弃堆末尾的最大值7
然后让剩下的数继续做heapify,周而复始直到堆减为0结束
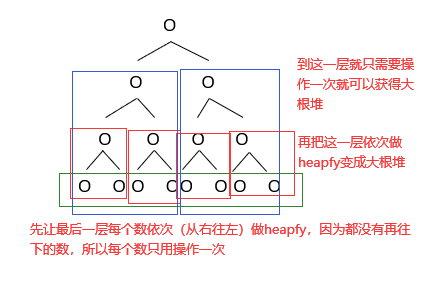
更优化的方式获取大根堆
如果我们已经知道数组中的所有数,并且只需要得到大根堆(不做别的操作)
tips:
1、堆结构底层是由数组支持实现的,如果堆在不断扩大的过程中超过了数组的长度,那么数组要成倍的加长
例如,原来的数组长度是100,用完之后系统会直接给它加到200,再用完就变成400
这样,算法的空间复杂度仍然不变
2、高级语言自带的堆方法只是一个黑盒,我们可以通过add和poll与之交互,本质就是我给它一个数,它给我一个数
虽然这样在简单场景下高效,但是针对一些具体问题就不好用了
比如,我想从已经规定好的堆结构里取一个数,然后让堆仍然保持大/小根堆,自带的堆方法效率很低,只能自己手写一个
这就是为什么面试的时候经常会要求手写堆结构的原因
比较器
1)比较器的实质就是重载比较运算符
2)比较器可以很好的应用在特殊标准的排序上
3)比较器可以很好的应用在根据特殊标准排序的结构上
在C++里也叫重载运算符
简单来说,就是在比较数的时候自定义一些的规则,让比较结构变成我们想要的
例子1,
比如我调用了.sort()方法去给数组排序
排序的本质就是比较数的大小
如果上面都不加,系统可能默认从大到小排出结果
但是,我现在希望从小到大(或者指定哪些数先排等一些更复杂的排序)排,那么我就可以传一个比较器给.sort()
.sort()就可以按照比较器规定的方式进行排序(比较)
例子2,
PriorityQueue是java中的优先级队列结构(也就是系统提供的堆方法)
当不指定时,默认生成的是小根堆
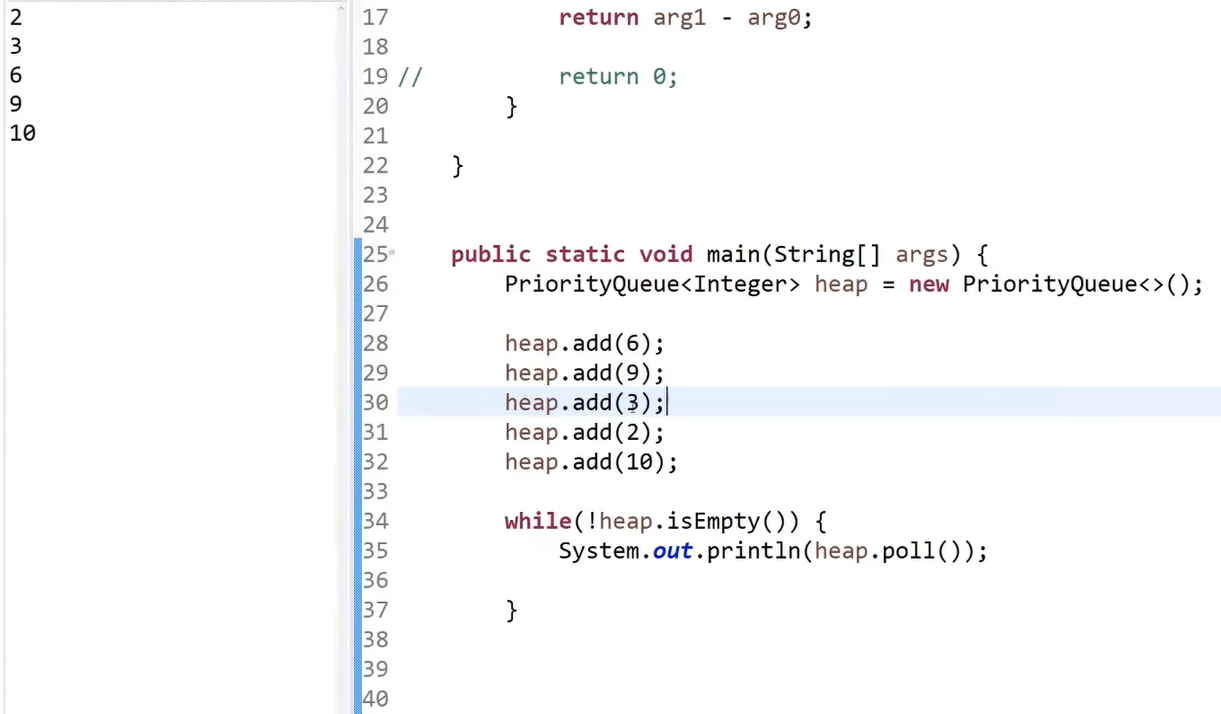
往里面添加数后poll,会按照从小到大的顺序返回值
此时,给它传一个比较器如下


这样PriorityQueue就会以大根堆的方式去构建了
比较器的应用场景
可以用于定义复杂的比较策略
例如,
我有两个数据:班级和年龄
如果想让整个数组整体按年龄来排序(小的在前),但是年龄一样的时候,班级大的排在前面
这时候可以定义比较器去实现(代码量少)
tips:
到目前为止,所有的排序算法都是基于"比较"进行的排序
也有不依靠"比较"进行的排序,但需要针对数据进行定制,往往只在特定情况下高效,使用范围较小
桶排序(基数排序)
桶排序思想下的排序
1)计数排序
2)基数排序
分析:
1)桶排序思想下的排序都是不基于比较的排序
2)时间复杂度为0(N),额外空间负载度0(M)
3)应用范围有限,需要样本的数据状况满足桶的划分
假设有以下数
[17,13,25,100,72]
里面最大的是三位数,所以其他的数要补成三位
[017,013,025,100,072]
现在设置一些“桶”用于存放数据(桶的底层一般是队列、数组或栈,这里用的是队列)
因为是十进制的数,所以理论上最多需要十个“桶”
具体到当前问题,实际上只用了0、1、2、3、5、7这几个
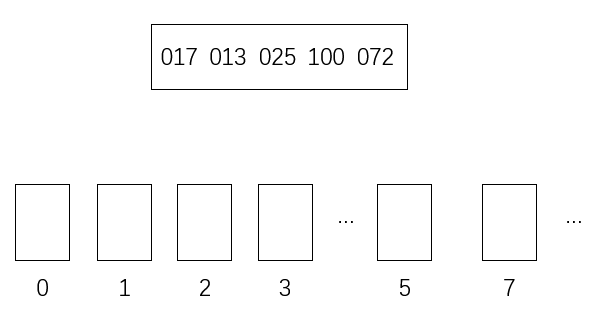
然后,从左到右按个位数将数放入桶里
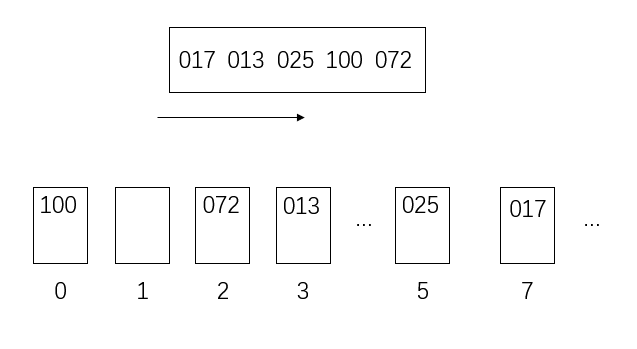
然后把桶里的数从左往右倒出来,数组更新
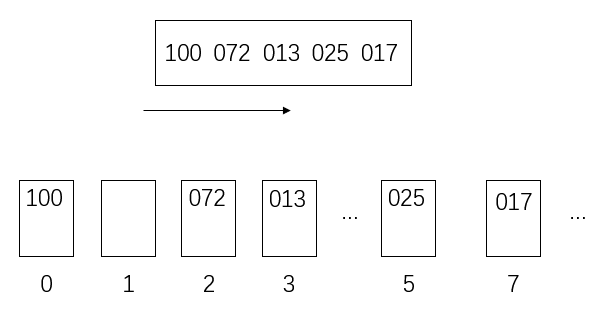
再从左到右按十位数将数放入桶里
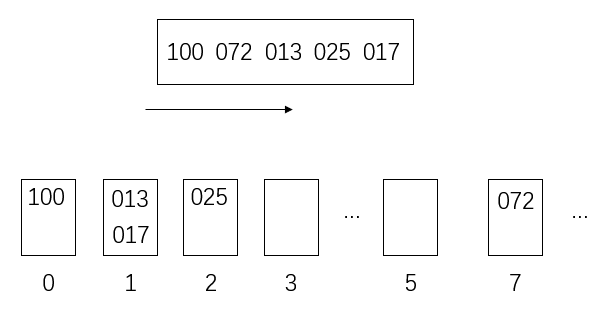
更新
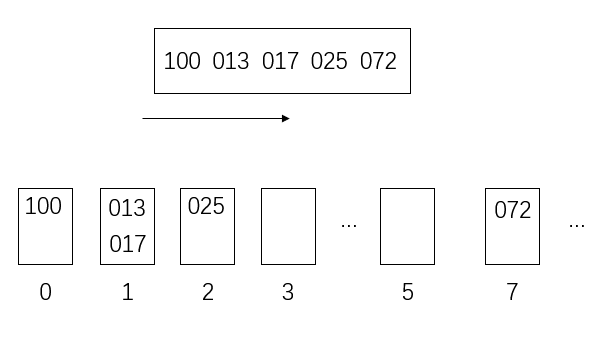
最后按百位数将数放入桶里
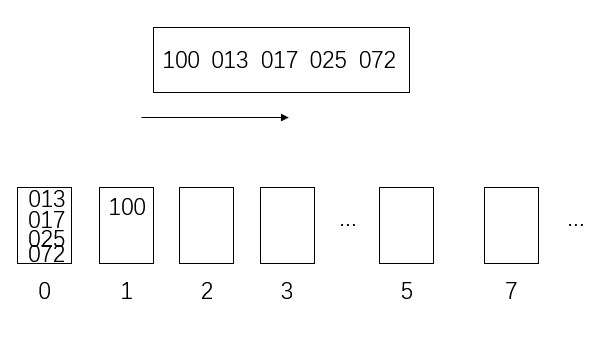
更新

排序结束
因为高位数是晚排序的,所以它优先级就会高,因此就会跑到最右边去
同理可区分十位和个位
代码实现讲解(2:11:25):https://www.bilibili.com/video/BV13g41157hK?p=5&spm_id_from=333.880.my_history.page.click


 浙公网安备 33010602011771号
浙公网安备 33010602011771号