【算法day3】小和、荷兰国旗、快排
小和问题
现有数组[1,3,4,2,5]
1左边是0(小于1),所以1的小和为0
3左边是1(小于3),所以3的小和为1
4左边是1、3(均小于4),所以4的小和为1+3=4
2左边是1、3、4(只有1小于2),所以2的小和为1
5左边是1、3、4、2(均小于5),所以5的小和为1+3+4+2=10
数组的小和为0+1+4+1+10=16
上述方法是从“左边有几个数比当前数小”的角度去解决
还可以转化为“右边有几个数比当前数大”来解
现有数组[1,3,4,2,5]
1右边有4个数大于1,有4个小和(4);
3右边有2个数大于3,有2个小和(6);
4右边有1个数大于4,有1个小和(4);
2右边有1个数大于2,有1个小和(2);
5右边没有(0)
4+6+4+2+0=16
荷兰国旗问题
问题一
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度O(N)
思路:
准备一个变量表示小于等于num的右边界【num定为5算了】
≤)[3,5,6,7,4,3,5,8]
↑
i
此时有两种逻辑:
1、 当前数[i]≤num,则把当前的数[i]和小于等于区域"≤)"中的下一个数交换,然后"≤)"向右扩,i++;
2、当前数[i]>num,直接跳下一个数,i++;
≤)[3,5,6,7,4,3,5,8]
↑
i
当指针来到3时,3≤5,区域"≤)"向右扩,i++
≤[3),5,6,7,4,3,5,8]
↑
i
≤[3,5),6,7,4,3,5,8]
↑
i
到5时同理
到6时满足第二种条件,直接跳下一个数,i++
≤[3,5),6,7,4,3,5,8]
↑
i
≤[3,5),6,7,4,3,5,8]
↑
i
到7时同理,直接跳下一个数,i++
到4时满足条件1,把4与"≤)"区域的下一个数交换,4与6交换,区域"≤)"向右扩,i++
≤[3,5),4,7,6,3,5,8]
↑
i
≤[3,5,4),7,6,3,5,8]
↑
i
≤[3,5,4),7,6,3,5,8]
↑
i
以此类推,当区域"≤)"扩到整个数组范围时结束
问题二(荷兰国旗问题)
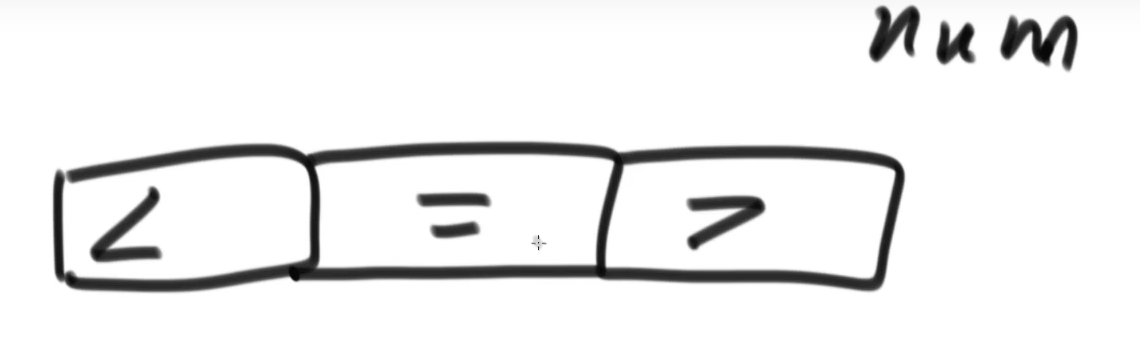
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度0(N)
思路:
还是跟前一个问题类似,准备两个变量,一个表示小于5的右边界,另一个表示大于5的左边界
<)[3,5,6,3,4,5,2,6,9,0](>
↑
i
此时每来到一个置就会有3种情况
1、当前数[i]<num,则把当前的数[i]和小于区域"<)"中的下一个数交换,然后"<)"向右扩,i++;
2、当前数[i]=num,,直接跳下一个数,i++;
3、当前数[i]>num,则把当前的数[i]和大于区域">)"中的前一个数交换,然后">)"向左扩,i++;
当指针来到3时,3<5,区域"<)"向右扩,i++
<[3),5,6,3,4,5,2,6,9,0](>
↑
i
<[3),5,6,3,4,5,2,6,9,0](>
↑
i
当指针来到5时,等于5,直接跳下一个
<[3),5,6,3,4,5,2,6,9,0](>
↑
i
<[3),5,0,3,4,5,2,6,9,6](>
↑
i
<[3),5,0,3,4,5,2,6,9,(6]>
↑
i
当指针来到6时,6>5,6和大于区域">)"中的前一个数交换,6和0交换,i原地不动(因为还没检查过它)
此时,检查新交换到i位置的数,发现其<5,则0和小于区域"<)"中的下一个数交换,然后"<)"向右扩,i++;
<[3),5,0,3,4,5,2,6,9,(6]>
↑
i
<[3),0,5,3,4,5,2,6,9,(6]>
↑
i
<[3,0),5,3,4,5,2,6,9,(6]>
↑
i
以此类推,当i遇到大于区域的边界时停止
最后两边就剩下大于小于的区域,而中间是等于的
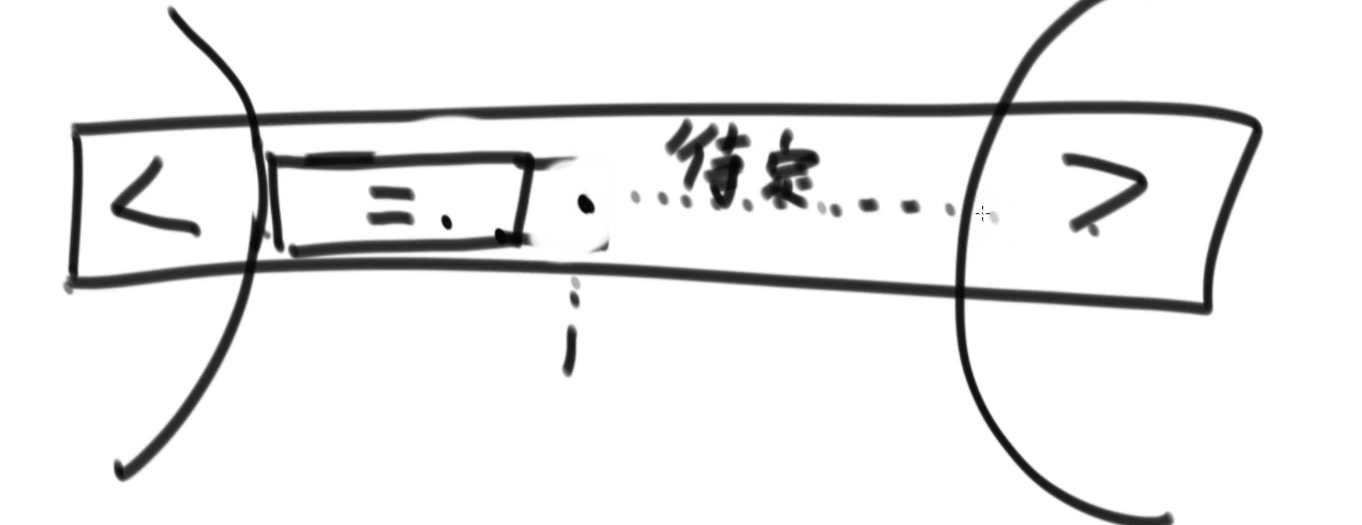
结束
快排
1.0版
例如
现在有一个数组,拿数组的最后一个数作为划分值

然后让它前面的一段做到左边的为≤num,右边的为>num,设num为5吧
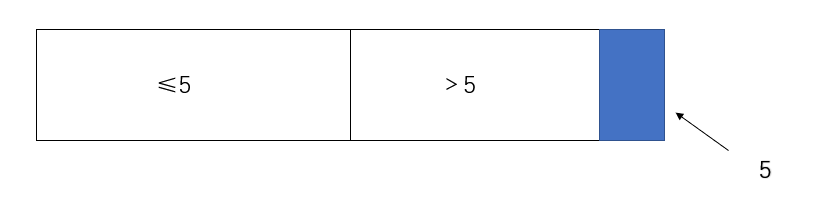
然后5和大于区域的第一个数做交换
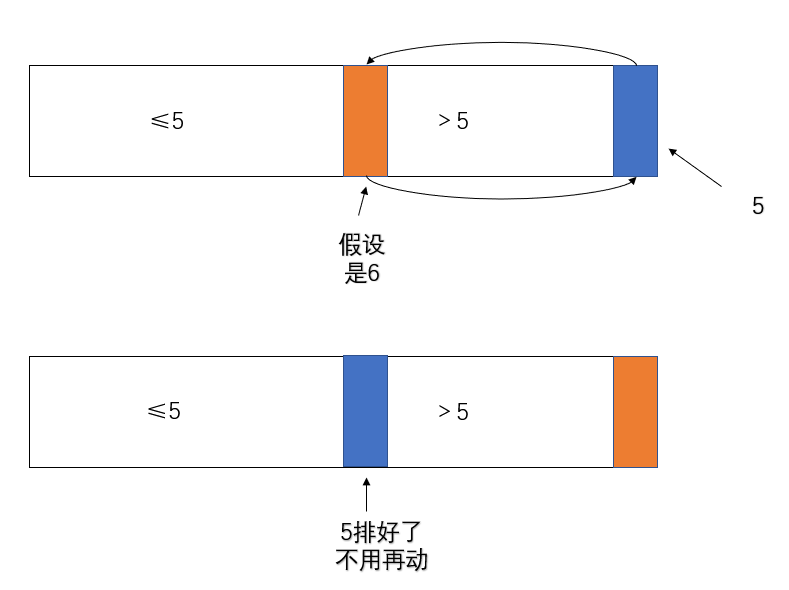
然后再把圈上的区域再重复进行之前的操作(拿最后一个数作为划分值)
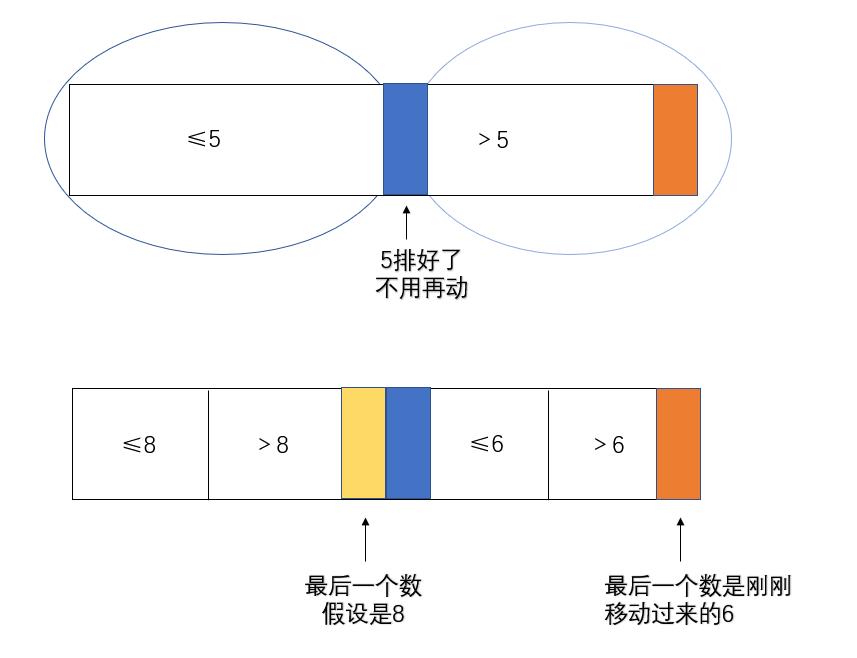
例如:
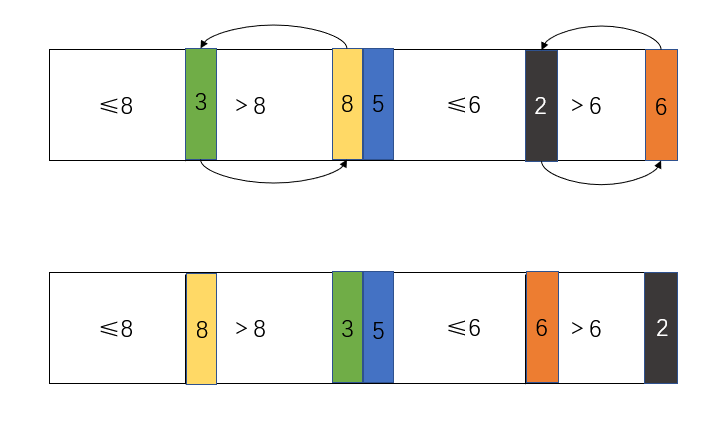
因为每次只保证一个数排好,所以递归到最后一定是有序的
2.0版
是以荷兰国旗问题为基础,也是最开始选数组的最后一个数作为划分值,不同的是,每次排完数组中间都是等于划分值的数,相当于每次搞定一批数的排序。
然后再在小于和大于区域重复上述操作直到排序结束
以5为例子
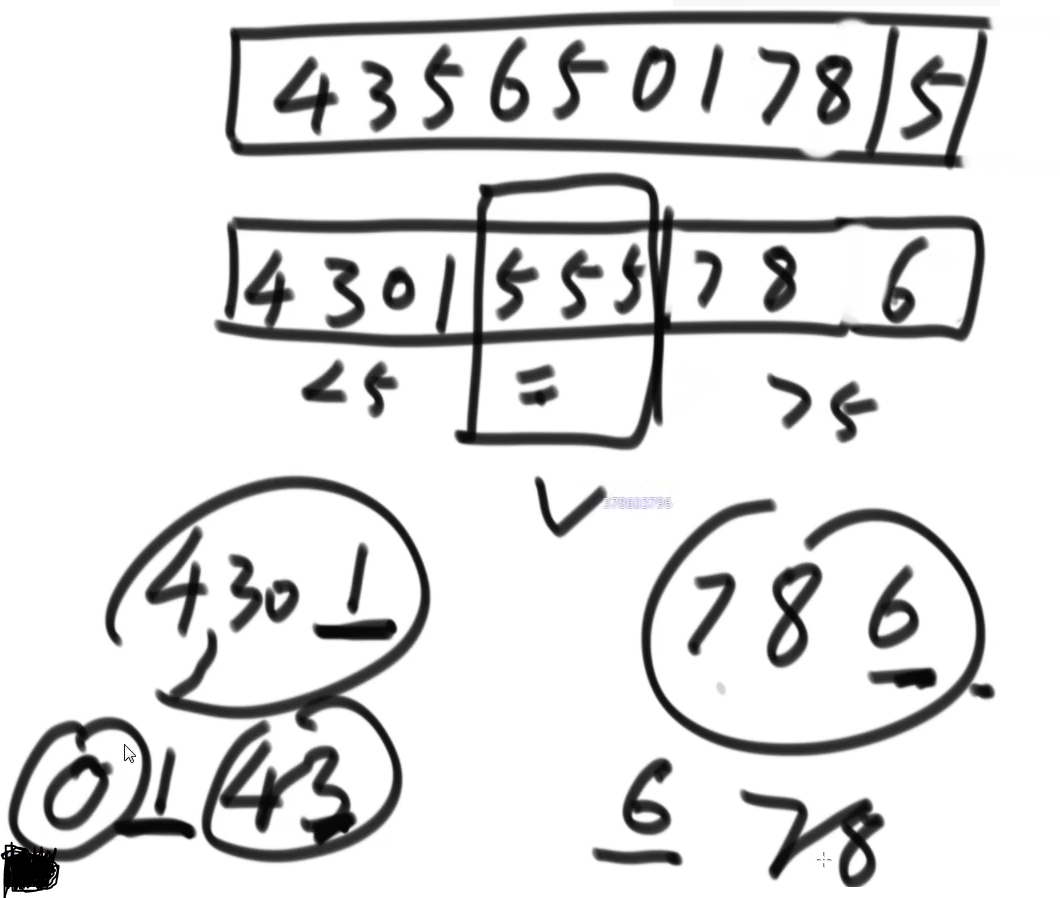
2.0和1.0在一些人为构建的数据中有可能会存在复杂度降低(好情况)或变高(坏情况)的情况
3.0版
在数组中随机选一个数作为划分值,将该数与数组最后一个数做交换再划分
由此,划分时出现好情况和坏情况就变成了概率事件,而且是等概率事件,因此该算法通过数学计算后的显示复杂度为O(Nlog2N)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号