【算法day2】复杂度和简单排序算法（2）
插入排序
有以下数组
数组：[2,4,3,6,1]
序号：[0,1,2,3,4]
第一次排序（范围0~0）：2左边没东西，不动
第二次排序（范围0~1）：4左边是2,4大不动
第三次排序（范围0~2）：3左边是4,移动，再左边是2，3大不动
第四次排序（范围0~3）：以此类推，直到排序结束
这个过程有点像拿扑克牌，把抽到的牌插到适合的地方
注：算法的时间复杂度是按照其最差情况下的来算的
插入排序与冒泡排序之间的区别：https://www.cnblogs.com/AraragiTsukihi/p/6339928.html
二分法
1)在一个有序数组中，找某个数是否存在【经典二分】
方法1：遍历（时间复杂度O(N)）
方法2：二分法（时间复杂度O(log2N)）
设要找的数是num，每次取数组的中间值x与num比较
若x>num，那么数组中位于x右边的数不用找了，在x左边继续取中间值比较
若x<num，那么数组中位于x左边的数不用找了，在x右边继续取中间值比较
若x=num,...
直到找到num
2）在一个有序数组中，找>=某个数最左侧的位置
3）局部最小值问题【一般二分用于有序情况，但无序也可以用】
局部最小定义：
在一个无序数组中，人格相邻数一定不相等
- 对于0位置的数（a），如果其小于1位置的数（b），那么0位置处局部最小
- 对于N-1位置的数,如果其小于N-2位置的数,那么N-1位置处局部最小
- 对于中间位置的数i，它同时比左边的数i-1和右边的数i+1小，那么i位置处局部最小
例：在无序数组中找到一个局部最小值
先做两个判断：
0位置是否存在局部最小；（有就直接返回0位置）
N-1位置是否存在局部最小；（有就直接返回N-1位置）
若上述局部最小不存在，则0位置到N-1位置上比存在局部最小
再取中间位置M，判断局部最小是否存在（有就直接返回M位置）
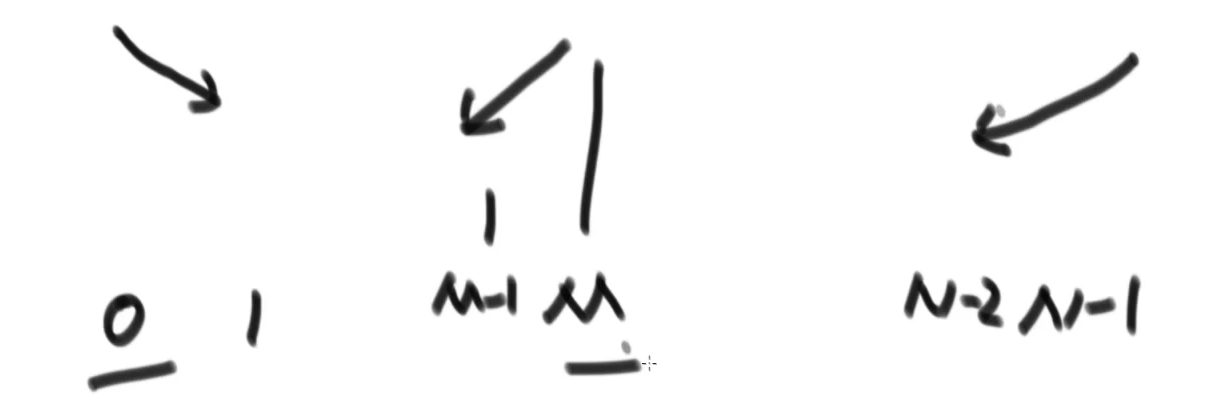
若上述局部最小不存在，取M的左边或者右边继续二分，直到找出一个局部最小即可
