【算法day1】复杂度和简单排序算法（1）
复杂度和简单排序算法
时间复杂度
以一个排序（选择排序）操作举例
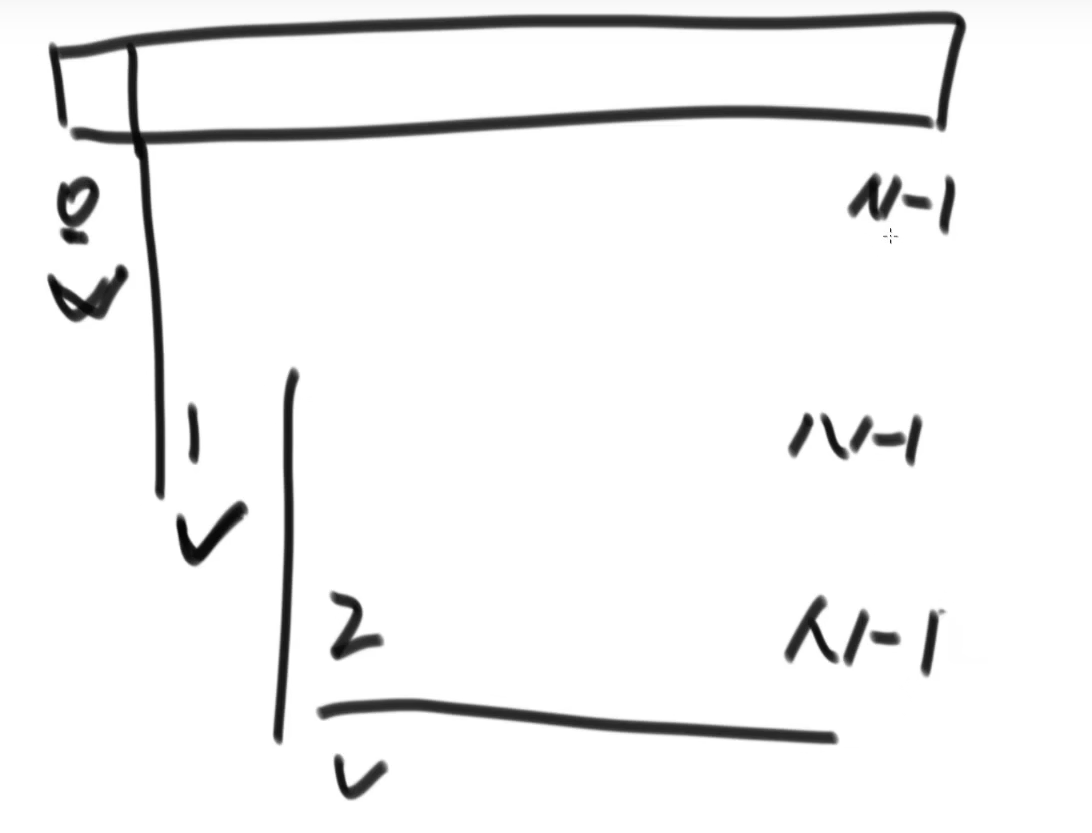
假设我有一个数组，我要找出其中的最小值放到0的位置上
那么
第一次我会遍历数组中N个数（在0位置处），找出最小的数交换到0位置【看了（寻址）N次，比较N次，一次交换】
第二次我会看遍历数组中N-1个数（在1位置处），找出最小的数交换到1位置【看了（寻址）N-1次，比较N-1次，一次交换】
第三次我会看遍历数组中N-2个数（在2位置处），找出最小的数交换到2位置【看了（寻址）N-2次，比较N-2次，一次交换】
以此类推，遍历的范围会缩小，数也按从小到大排好
总结一下：
一共看了N+(N-1)+(N-2)+(N-3)+...次（等差数列）
一共比了N+(N-1)+(N-2)+(N-3)+...次（等差数列）
一共换了N次
上述对常数的操作次数加起来可以写成：aN2+bN+C
那么时间复杂度就是在常数操作数量级的表达式（上式）中，最高次项的次数，例如上面这个排序的时间复杂度就是O(N2)
异或
结论：
1、0异或N对于N
2、N异或N对于0
3、满足交换、结合律
4、一批数要异或在一起，那么不论先后顺序，得到的结果是一样的
快速交换a、b的值
int a = 甲；int b = 乙；
那么只需
a = a⊕b;(a = 甲⊕乙,b = 乙)
b = a⊕b;(a = 甲⊕乙,b = 甲⊕乙⊕乙 = 甲)
a = a⊕b;(a = 甲⊕乙⊕甲 = 乙,b = 甲)
便可完成a、b交换(不用额外申请空间，前提是a、b指向两个不同的内存空间)
找奇偶数
问题描述：
在一个数组中
1、只有一个数出现奇数次，其余的出现偶次，把它找出来
2、有两个数出现奇数次，其余的出现偶次，把它找出来并且给出这两个数是什么
要求时间复杂度为O(N),空间复杂度为O(1)
思路：
1、第一种情况
准备一个数int eor = 0
用eor把数组从头异或到尾
假如数组是[a,b,c,...]
那么
eor = eor⊕a；
eor = eor⊕b；
eor = eor⊕c；
...
最后eor 就是出现次数为奇数的那个数
例如数组为[2,1,3,1,3,1,3,2,1]
用eor去异或，最后结果一定是3
因为上述数组在以后时无需考虑顺序，数组可看成
[1,1,1,1,2,2,3,3,3]
4个1异或完是0；
2个2异或完是0；
3个3异或完是它本身（3）；
结束
2、第二种情况
设这两个出现奇数次的数是a和b，并且我们知道两者不等
准备一个数int eor = 0
用eor把数组从头异或到尾，那么最后eor = a⊕b
先跟所有的偶数次的异或得到0，然后跟奇数次的a异或得a，再跟奇数次的b异或剩个b，最后成了a⊕b
因为a不等于b，所以eor不等于0，所以eor一定在某一位上不等于0（为1）
假设eor是在第8位上不为0，那么a和b的第8位一定是不一样的
再准备一个变量eor2
只有当数组中某个数的第8位是0（或者1），才把这个数同eor2异或，那么最后eor2会等于a或b的其中一个
之后再用eor异或eor2就可以得到另一个数
tips：
怎么着某一位是指定数的数？（比如第8位是1）
这个问题可以归结成：提取出最右侧的1
假设
k：1010111100
k取反：010100011
k取反+1：010100100
k&k取反+1 = 000000100，提取得到最右侧的1
在位运算中，需要把一个数最右侧的1提取出来
只需将这个数和它自身取反后加1的结果做与运算即可
结束
