钢条切割问题带你彻底理解动态规划
动态规划 （Dynamic Programming）
什么是动态规划?
动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一个子问题的解推出。
动态规划和分治法相似，都是通过分解，求解，并组合子问题来求解原问题。分治法将问题划分成相互独立互不相交的子问题，递归求解子问题，再将它们的解组合起来，求出原问题的解。与之相反，动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题。在这种情况下，分治算法会做出许多不必要的工作，它会反复的求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次，将结果保存到表格（数组）中，从而无需每次求解一个子子问题都要重新计算。
动态规划之钢条切割问题
假定我们知道某公司出售一段长度为i英寸的钢条的价格为p[i](i=1,2,3….)钢条长度为整英寸如图给出价格表的描述（任意长度的钢条价格都有）
现在先给一段长度为n的钢条，问怎么切割，获得的收益最大 rn?
考虑n=4的时候，有以下8种切割方式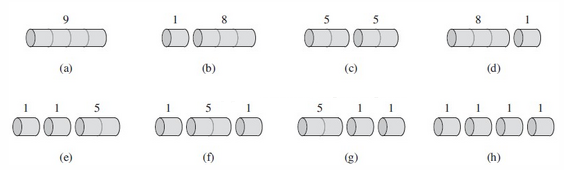
假如一个最优解把n段切成了k段（1<=k<=n）,那么最优切割方案：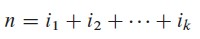
i及下标表示第i段的长度，n为钢条的总长度。
最大收益：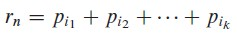
p及下标表示第i段的收益，r为钢条的总收益。
接下来对这个问题进行求解，我们先用普通的递归方法求解：
我们从钢条的左边切下长度为i的一段，只对右边剩下长度为n-i的一段继续进行切割，对左边的不再切割。
这样，当第一段长度为n的时候，收益为p[n]，剩余长度为0，收益为0（这也是递归的基本问题），对应的总收益为p[n]。
当第一段长度为i的时候，收益为p[i]，剩余长度为n-i，对应的总收益为p[i]加上剩余的n-i段再进行当第一段长度为i的时候，收益为p[i]，剩余长度为n-i-i，....直到剩余长度为0，收益为0。
所以递归方程式为：
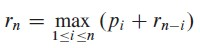pi就是就是p[i],可以看出每次都要进行从1到n的遍历。
代码实现 - 自顶向下递归实现
1 #include <iostream> 2 int UpDown(int n, int * p)//参数n是长度，参数p是价格表 3 { 4 if (n == 0) return 0;//递归的基本问题 5 int tempMaxPrice = 0; 6 for (int i = 1; i < n + 1; i++) 7 { 8 int maxPrice = p[i] + UpDown(n - i, p); 9 if (maxPrice > tempMaxPrice) 10 { 11 tempMaxPrice = maxPrice; 12 } 13 } 14 return tempMaxPrice; 15 } 16 int main() 17 { 18 int p[11]{ 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };//索引代表 钢条的长度，值代表价格 19 std::cout << UpDown(4,p) <<std::endl; 20 }
动态规划的方法进行求解
上面的方法之所以效率很低，是因为它反复求解相同的子问题。比如求r[9]和r[8]的时候都求解了r[7],就是说r[7]被求解了两次。因此，动态规划算法安排求解的顺序，对每个子问题只求解一次，并将结果保存到数组中。如果随后再次需要此子问题的解，只需查找保存的结果，不必重新计算。因此动态规划的方法是付出额外的内存空间来节省计算时间。
动态规划有两种等价的实现方法（我们使用上面的钢条切割问题为例，实现这两种方法）
第一种方法是 带备忘的自顶向下法：
此方法依然是按照自然的递归形式编写过程，但过程中会保存每个子问题的解（通常保存在一个数组中）。当需要计算一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了计算时间；如果没有保存过此解，按照正常方式计算这个子问题。我们称这个递归过程是带备忘的。
代码实现 - 自顶向下动态规划实现
1 #include <iostream> 2 int result[11]{ 0 }; 3 int UpDown(int n, int* p)//求得长度为n的最大收益 4 { 5 if (n == 0) return 0; 6 if (result[n] != 0)//这里直接返回记录的结果 7 { 8 return result[n]; 9 } 10 int tempMaxPrice = 0; 11 for (int i = 1; i < n + 1; i++) 12 { 13 int maxPrice = p[i] + UpDown(n - i, p); 14 if (maxPrice > tempMaxPrice) 15 { 16 tempMaxPrice = maxPrice; 17 } 18 } 19 result[n] = tempMaxPrice;//将计算过的长度为n的钢条切割的最大收益记录起来 20 return tempMaxPrice; 21 } 22 int main() 23 { 24 int p[11] = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };//索引代表 钢条的长度，值代表价格 25 std::cout << UpDown(4,p); 26 }
第二种方法是 自底向上法（常用的方法）：
首先恰当的定义子问题的规模，使得任何问题的求解都只依赖于更小的子问题的解。因而我们将子问题按照规模排序，按从小到大的顺序求解。当求解某个问题的时候，它所依赖的更小的子问题都已经求解完毕，结果已经保存到了数组中。
代码实现 - 自底向上动态规划实现
1 #include <iostream> 2 int result[11]{ 0 }; 3 int BottomUp(int n, int* p) 4 { 5 for (int i = 1; i < n + 1; i++) 6 { 7 int tempMaxPrice = 0; 8 for (int j = 1; j <= i; j++)//下面取得 钢条长度为i的时候的最大收益 9 { 10 int maxPrice = p[j] + result[i - j]; 11 if (maxPrice > tempMaxPrice) 12 { 13 tempMaxPrice = maxPrice; 14 } 15 } 16 result[i] = tempMaxPrice; 17 } 18 return result[n]; 19 } 20 int main() 21 { 22 23 int p[11] = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };//索引代表 钢条的长度，值代表价格 24 std::cout << BottomUp(4,p); 25 }
可以看出自顶向下的动态规划求解和普通的递归求解差不多，不过动态规划递归调用时带了备忘录，记录了已经解决的问题，所以对于上文提到的r[7]，我们只求解了一次。
自底向上的动态规划也用了备忘录，不过它只是迭代求解，并没有进行递归，所以这也是我们常用方法。
以上有什么不足的地方和应该改进的地方，欢迎各路大神批评指正，笔者一定虚心接受。谢谢！
