JZ043:往完全二叉树添加节点

------------恢复内容开始------------

title: 往完全二叉树添加节点

---

📃 题目描述

题目链接：往完全二叉树添加节点

🔔 解题思路

方法一：空间换时间的思想，采用层次遍历，遍历到第一个可插入 节点的 父节点，证明后续的节点都是可以作为父节点插入数据的，保存在队列中，如图：

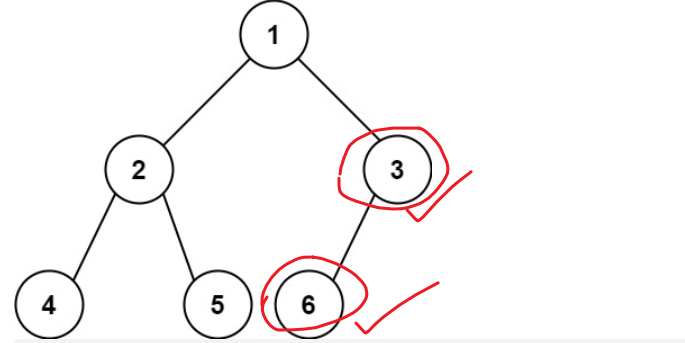
节点3就是可插入数据的第一个节点，节点6就是可插入数据的第二个节点；

class CBTInserter {
public:
    CBTInserter(TreeNode* root) : _root(root){
        _addPos.push(root);
        while (!_addPos.empty()) {
            int len = _addPos.size();
            bool last = false;//是否遍历到可插入的 叶子节点的父节点；
            for (int i = 0; i < len; i++) {
                TreeNode *tmp = _addPos.front();
                if (tmp->left !=nullptr) _addPos.push(tmp->left);
                if (tmp->right !=nullptr) _addPos.push(tmp->right);

                //如果左右孩子存在空，证明就是 可插入的 叶子节点的父节点；
                if (tmp->left == nullptr || tmp->right == nullptr) {
                    last = true;
                    break; //跳出循环，后序都是可插入的节点
                }
                _addPos.pop();//弹出不可插入的节点 
            }
            if (last == true) break;
        }
    }
    
    int insert(int v) {
        TreeNode *tmp = new TreeNode(v);
        TreeNode *cur = _addPos.front();
        if (cur->left == nullptr) {            
            cur->left = tmp;
        }
        //如果右边为空的话，证明这个节点已经无效了
        else if (cur->right == nullptr) {
            cur->right = tmp;
            _addPos.pop();
        }
        _addPos.push(tmp);
        return cur->val;
    }
    
    TreeNode* get_root() {
        return _root;
    }
private:
    TreeNode *_root;
    queue<TreeNode*> _addPos;
};

💥 复杂度分析

• 时间复杂度：o(1);
• 空间复杂度：O(n);

------------恢复内容结束------------