布隆过滤器概念及其公式推导 转载
公式推导内容转自博客 https://blog.csdn.net/houzuoxin/article/details/20907911
布隆过滤器概念
数据如何存入布隆过滤器
布隆过滤器是由一个很长的二进制矢量和一系列哈希函数组成的。
二进制矢量本质是一个位数组:数组的每个元素都只占1bit空间,并且每个元素只能为0或1。
布隆过滤器还拥有k个哈希函数,当一个元素加入布隆过滤器中的时候,会使用k个哈希函数对其进行k次计算,得到k个哈希值,并且根据得到的哈希值,在维数组中把对应下标的值置位1。
若要判断这个数是否在布隆过滤器中,就对该元素进行k次哈希计算,得到的值在位数组中判断每个元素是否都为1,如果每个元素都为1,就说明这个值在布隆过滤器中。
误判情况
布隆过滤器只能插入不能删除,所以插入的元素越来越多时,当一个不在布隆过滤器中的元素,经过同样规则的哈希计算之后,得到的值在位数组中查询,有可能这些位置因为其他的元素先被置1了。所以布隆过滤器存在误判的情况,但是如果布隆过滤器判断某个元素不在布隆过滤器中,那么这个值就一定不在。
如何补救这个情况呢,可以设立白名单,存储可能会被误判的元素。
综上所述,布隆过滤器可精确的代表一个集合,可精确判断某一元素是否在此集合中,精确程度由用户的具体设计决定,达到100%的正确是不可能的。但是布隆过滤器的优势在于,利用很少的空间可以达到较高的精确率。
实际应用面试题
不安全网页的黑名单包含100亿个黑名单网页,每个网页的URL最多占用64字节。现在想要实现一种网页过滤系统,可以根据网页的URL判断该网站是否在黑名单上,请设计该系统。要求该系统允许有万分之一以下的判断失误率,并且使用的额外空间不要超过30G。
解题:布隆过滤器的bitarray大小如何确定?
- 设bitarray大小为m,样本数量为n,失误率为p。
- 由题可知 n = 100亿,p = 0.01%
- 单个样本大小不影响布隆过滤器大小,因为样本会通过哈希函数得到输出值。
- 使用样本数量n和失误率p可以算出m,公式为:
![公式]()
- 求得 m = 19.19n,向上取整为 20n。所以2000亿bit,约为25G。
- 所使用哈希函数个数k可以由以下公式求得:
![公式]()
- 所以 k = 14,即需要14个哈希函数。
- 通过 m = 20n, k = 14,可以通过以下公式算出设计的布隆过滤器的真实失误率为0.006%。
![公式]()
公式推导
上面那些公式是怎么来的呢,很多地方都只写明了公式,但是没有解释公式怎么推导出来的。最终终于找到一个大佬写的很详细的推导过程,绝对看得懂,转自https://blog.csdn.net/houzuoxin/article/details/20907911,但是为了方便自己后续复习,所以现在将推导过程截图贴置这里,做一个大佬的搬运工。
误判概率即失误率的证明和计算
下面的图中红色框里,你可以看到 布隆过滤器长度m、误判率p 以及 哈希函数个数k 的求解过程。




其他使用场景
- 网页爬虫对URL的去重,避免爬去相同的URL地址
- 垃圾邮件过滤,从数十亿个垃圾邮件列表中判断某邮箱是否是杀垃圾邮箱
- 解决数据库缓存击穿,黑客攻击服务器时,会构建大量不存在于缓存中的key向服务器发起请求,在数据量足够大的时候,频繁的数据库查询会导致挂机。


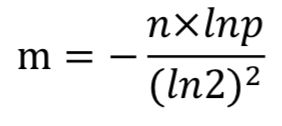
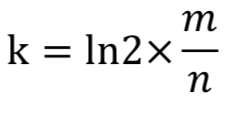
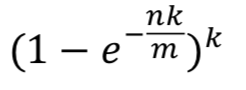

 浙公网安备 33010602011771号
浙公网安备 33010602011771号