[HNOI2017]礼物

因为可以加上一个常数C，说是非负整数，但其实A手环加上，就等于B手环减去，于是把m范围扩充到[-100,100]即可。

然后所求变为：

$$\sum (x_i-y_i+C)$$

接着拆开，可以得到：

$$\sum(x_i^2+y_i^2+C^2)+2*C*\sum(x_i-y_i)+2*\sum(x_i*y_i)$$

然后发现这些有常量，可变的C所对应的x和y是常数，而与顺序有关的x_i*y_i又是与C无关的。所以我们可以先求出的最大值x_i*y_i。如果我们将B手环在输入之后反转一下，可以发现当翻转前A与B发生错位之时，每一个错位都可以对应反转之后的B与A的FFT的乘积的各个项的系数。

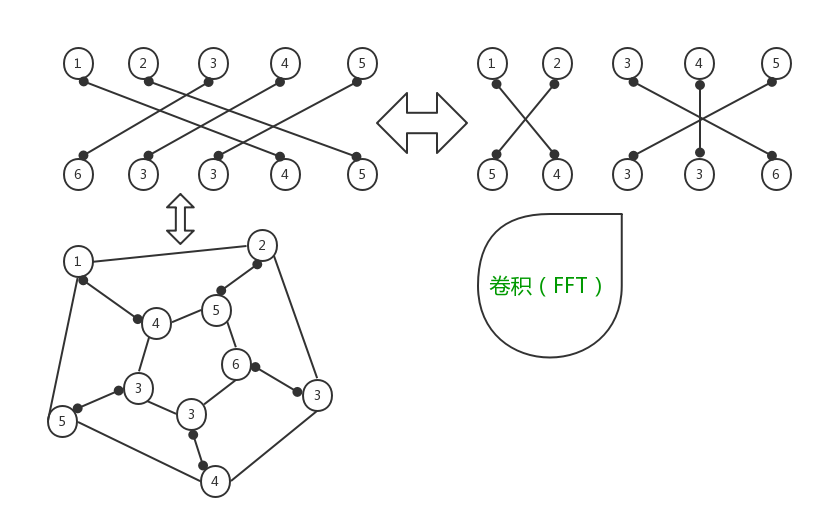
 然后再枚举C从[-m,m]那么答案就出来了。

不会FFT的就去学吧。

#include<cmath>
#include<cstdio>
#include<complex>
#include<iostream>
#include<algorithm>
#define C complex<double>
#define pf(a) ((a)*(a))
using namespace std;
const int MAXN=1000000,INF=0x3f3f3f3f;
const double pi=acos(-1.0);
int n,m,L,G,Max,Val,ans=INF,sum1,sum2;
int R[MAXN],V[MAXN];
C A[MAXN],B[MAXN];
inline int gi(){int res; scanf("%d",&res); return res;}
void FFT(C *a,int p)
{
  for(int i=0;i<n;i++)if(i<R[i])swap(a[i],a[R[i]]);
  for(int i=1;i<n;i<<=1)
    {
      C wn(cos(pi/i),sin(p*pi/i)),x,y;
      for(int j=0;j<n;j+=(i<<1))
        {
          C w(1,0);
          for(int k=0;k<i;k++,w*=wn)
            {
              x=a[j+k],y=w*a[j+k+i];
              a[j+k]=x+y;
              a[j+k+i]=x-y;
            }
        }
    }
}
int main()
{
  freopen("gift.in","r",stdin);
  freopen("gift.out","w",stdout);
  n=gi();Max=gi(); n--;
  for(int i=0;i<=n;i++)A[i]=gi();
  for(int i=0;i<=n;i++)B[i]=gi();
  for(int i=0;i<=n;i++)
    {
      sum1+=pf(A[i].real())+pf(B[i].real());
      sum2+=A[i].real()-B[i].real();
    }
  m=n+n; reverse(B,B+n+1);
  for(n=1;n<=m;n<<=1)L++;L--;
  for(int i=0;i<n;i++)R[i]=(R[i>>1]>>1)|((i&1)<<L);
  FFT(A,1); FFT(B,1);
  for(int i=0;i<=n;i++)A[i]*=B[i];
  FFT(A,-1);
  for(int i=0;i<=m;i++)V[i]=(int)(A[i].real()/n+0.5);
  n=m/2; Val=V[n];
  for(int i=0;i<=n-1;i++)
    if(Val<V[i]+V[n+i+1])
      Val=V[i]+V[n+i+1];
  Val*=2;
  for(int c=-Max;c<=Max;c++)
    ans=min(ans,sum2*2*c+(n+1)*c*c-Val);
  printf("%d\n",ans+sum1);
  return 0;
}