斗地主

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

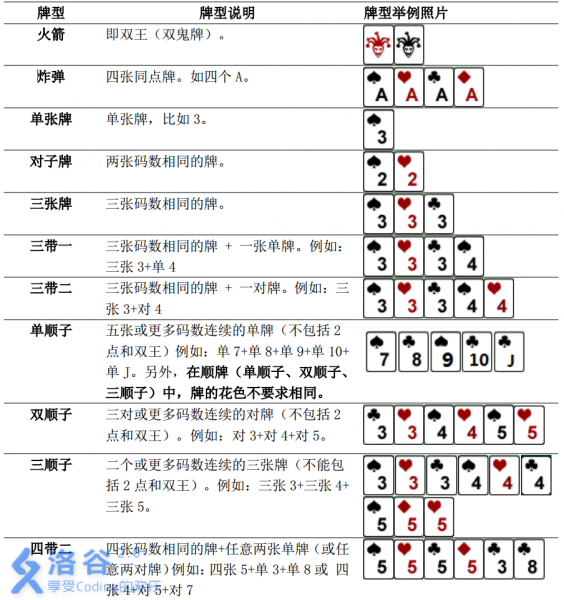
输入输出格式

输入格式：

 

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

 

输出格式：

 

共T行，每行一个整数，表示打光第i手牌的最少次数。

 

输入输出样例

输入样例#1：

1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

输出样例#1：

3

输入样例#2：

1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

输出样例#2：

6

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

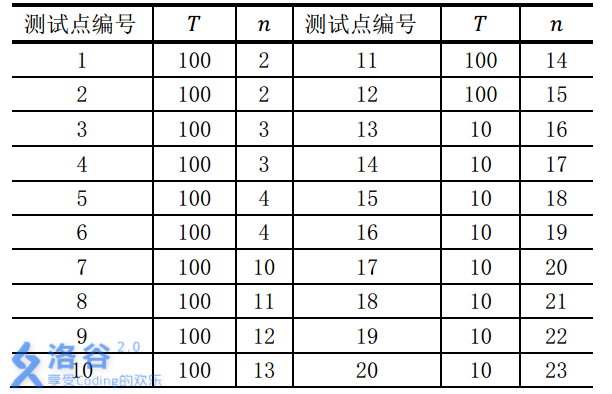
对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：

数据保证：所有的手牌都是随机生成的。

分析

仔细看，这道题着实想不到什么优美的算法，那么基本确定方向——dfs。 
先分析，这题的花色是没用的 
我们再分析，会发现这题的出牌顺序是不影响答案的 

首先我们把A存到a[12],把2存到a[13]中，这样处理顺子比较好处理

如果有四张的牌

首先我们肯定是带两张单牌比较优

然后是带两个对子优，之后是一个对子

因为对子组成顺子比单牌容易，所以优先搞单牌

三张的类似

然后枚举三种顺子

逐一枚举各种方案，去找最优解

因为顺子并不是越长越好的，打过斗地主的都知道吧

一个可行性剪枝是当现在的出牌的次数大于当前最优的方案就直接返回，不知道会快多少呢

每次的ans的初始值为23，因为最多的数据只有23张手牌，没有答案会比23大啦

#include <cstdio>
#include <iostream>
#include <algorithm> 
#include <cstring>
using namespace std;
int t,n;
int ans;
int a[16];
void in()
{
    memset(a,0,sizeof(a));//每次清零
    for(int i=1;i<=n;i++)
    {
      int x,y;
      scanf("%d%d",&x,&y); 
      if(x==0)
      a[14]++;
      if(x==1)
      a[12]++;
      if(x==2)
      a[13]++;
      if(x>=3)
      a[x-2]++;    
    }
} 
void dfs(int x)
{
    if(x>ans) return;
    int s1,s2,s3,s4;
    s1=s2=s3=s4=0;
    for(int i=1;i<=14;i++)//统计单牌与对子
    {
     if(a[i]==1) s1++;
     if(a[i]==2) s2++;
    }
    for(int i=1;i<=14;i++)//四带的牌
    if(a[i]==4) 
    { 
     s4++;
     if(s1>=2) s1-=2;
     else if(s2>=2) s2-=2;
     else if(s2>=1) s2--;
    }
    for(int i=1;i<=14;i++)//三带的牌
    if(a[i]==3)
    {
        s3++;    
        if(s1>=1) s1--;
        else if(s2>=1) s2--;
    }
    ans=min(ans,x+s1+s2+s3+s4);//手中没牌，更新方案
    int j;
    for(int i=1;i<=8;i++)//枚举单顺子，第一层枚举起点，第二层枚举长度
    {
     for(j=i;j<=12;j++)
      {
          a[j]--;
          if(a[j]<0) break;
          if(j-i>=4) dfs(x+1);
      }
      if(j==13) j--;
      while(j>=i) a[j--]++;//回溯过程
    } 
    for(int i=1;i<=10;i++)//枚举双顺子
    {
     for(j=i;j<=12;j++)
      {
          a[j]-=2;
          if(a[j]<0) break;
          if(j-i>=2) dfs(x+1);
      }
      if(j==13) j--;
      while(j>=i) a[j--]+=2;
    } 
    for(int i=1;i<=11;i++)//枚举三顺子
    {
     for(j=i;j<=12;j++)
      {
          a[j]-=3;
          if(a[j]<0) break;
          if(j-i>=1) dfs(x+1);
      }
      if(j==13) j--;
      while(j>=i) a[j--]+=3;
    } 
}
int main()
{
    scanf("%d%d",&t,&n);
    while(t--)
    {
        in();
        ans=23;
        dfs(0);
        printf("%d\n",ans);
    } 
    return 0;
}