Luogu 4001 [BJOI2006]狼抓兔子

BZOJ 1001……

并不会这个trick，所以笔记要详细一点。

前置知识 ： 平面图转对偶图    传送门

听说直接$Dinic$就好了，还跑得比正解快……

首先我们按照平面图的定义，把网格图中所有的平面以及另加的起点和终点在新图中标号，一共有$(n - 1) * (m - 1) * 2 + 2$个点，标完样例之后大概是这样子的：

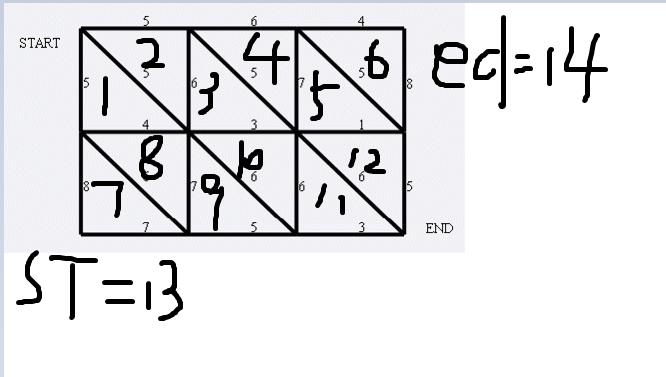
然后我们接着按照定义，把有相邻的边的点连上双向边，对于那些在边界上的边，我们分别选择和$st$和$ed$连边，具体来说是这样的：

红色的边和$st$连边，蓝色的边和$ed$连边，其他黑色的边和它相邻的两个联通块连边。

注意$n == 1$或者$m == 1$的时候其实是一条链的情况，只要把最小的边鸽掉就好了，这时候所有的边都是要从$st$出发连到$ed$的，但是我的写法会挂掉，所以需要拎出来特判一下。

容易发现这样子构图之后从$st$到$ed$的每一条路都对应了原图中左上角到右下角的一个鸽，这样子我们求一个最小鸽就变成了一个最短路，就能方便地跑过去了。

要注意一个细节就是说$st$和$ed$必须放在左下角和右上角（可以对调），因为我们在原图中是要从左上角到右下角求一个最小鸽，要不然就不代表从左上角到右下角的一个最小鸽了吧。

连完边之后的效果图大概是这个大神博客里面的样子。     戳这里

时间复杂度$O(nmlognm)$。

Code:

#include <cstdio>
#include <cstring>
#include <queue>
#include <iostream>
using namespace std;
typedef pair <int, int> pin;

const int N = 2e6 + 5;
const int M = 6e6 + 5;

int n, m, tot = 0, head[N], dis[N];
bool vis[N];

struct Edge {
    int to, nxt, val;
} e[M];

inline void add(int from, int to, int val) {
    e[++tot].to = to;
    e[tot].val = val;
    e[tot].nxt = head[from];
    head[from] = tot;
} 

inline void addEdge(int x, int y, int v) {
    add(x, y, v), add(y, x, v);
}

inline void read(int &X) {
    X = 0; char ch = 0; int op = 1;
    for(; ch > '9' || ch < '0'; ch = getchar())
        if(ch == '-') op = -1;
    for(; ch >= '0' && ch <= '9'; ch = getchar())
        X = (X << 3) + (X << 1) + ch - 48;
    X *= op;
}

priority_queue <pin> Q;
inline void dij(int st) {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    Q.push(pin(dis[st] = 0, st));
    for(; !Q.empty(); ) {
        int x = Q.top().second; Q.pop();
        if(vis[x]) continue;
        vis[x] = 1;
        for(int i = head[x]; i; i = e[i].nxt) {
            int y = e[i].to;
            if(dis[y] > dis[x] + e[i].val) {
                dis[y] = dis[x] + e[i].val;
                Q.push(pin(-dis[y], y));
            }
        }
    }
}

int main() {
//    freopen("5.in", "r", stdin);
    
    read(n), read(m);
    int st = (n - 1) * (m - 1) * 2 + 1, ed = st + 1;
    if(n == 1 || m == 1) {
        for(int i = 1; i <= n; i++)
            for(int j = 1; j < m; j++) {
                int val; read(val);
                addEdge(st, ed, val);
            }
        for(int i = 1; i < n; i++)
            for(int j = 1; j <= m; j++) {
                int val; read(val);
                addEdge(st, ed, val);
            }
        for(int i = 1; i < n; i++)
            for(int j = 1; j < m; j++) {
                int val; read(val);
                addEdge(st, ed, val);
            }
    } else {
        for(int i = 1; i <= n; i++)
            for(int j = 1; j < m; j++) {
                int val; read(val);
                if(i == 1) addEdge(ed, 2 * ((i - 1) * (m - 1) + j), val);
                if(i == n) addEdge(st, 2 * ((i - 2) * (m - 1) + j) - 1, val);
                if(i != 1 && i != n) addEdge(2 * ((i - 1) * (m - 1) + j), 2 * ((i - 2) * (m - 1) + j) - 1, val);
            }
        for(int i = 1; i < n; i++)
            for(int j = 1; j <= m; j++) {
                int val; read(val);
                if(j == 1) addEdge(st, 2 * ((i - 1) * (m - 1) + j) - 1, val);
                if(j == m) addEdge(ed, 2 * ((i - 1) * (m - 1) + j - 1), val);
                if(j != 1 && j != m) addEdge(2 * ((i - 1) * (m - 1) + j) - 1, 2 * ((i - 1) * (m - 1) + j) - 2, val);
            }
        for(int i = 1; i < n; i++)
            for(int j = 1; j < m; j++) {
                int val; read(val);
                addEdge(2 * ((i - 1) * (m - 1) + j) - 1, 2 * ((i - 1) * (m - 1) + j), val); 
            }
    }
    
    dij(st);
    
    printf("%d\n", dis[ed]);
    return 0;
}