Luogu 1268 树的重量

并不会这种构造题。

首先可以随意把一个叶子结点当作根，题目告诉了我们这样子不会改变答案。

然后我们考虑一个一个把叶子结点连到这一棵树里面去，对于每一个叶子结点，我们可以把它对答案的贡献看作它向根的连边的长度减去已经计算过的长度，相当于从一条已经连过的边拉出一条新的链把它连到树里面去，不容易发现只要对每一个连过的结点算一算贡献取最小值就可以了。

思考为什么这样子是对的。

随便画一个树：

 

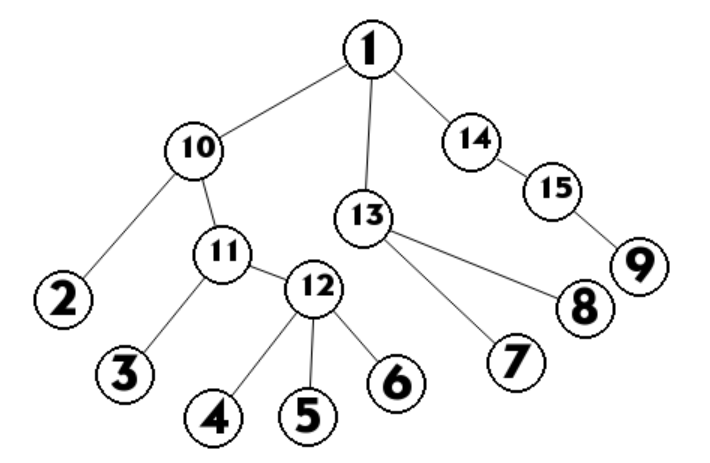
如图，$1$为根，假设$2,3,4,7$都已经算过了，现在要计算$5$的贡献，那么有：

$(2, 5) = (10, 11, 12, 5)$

$(3, 5) = (11, 12, 5)$

$(4, 5) = (12, 5)$

$(7, 5) = (1, 10, 11, 12, 5)$。

发现这个点到其他已经计算过的点的拉出的链其实是包含关系的，而多出来的部分其实在之前已经算过了，所以只要取最小值就是这个点的贡献了。

考虑一下怎么计算点的贡献，我们设根为$rt$，现在要从根到$x$的路径上拉出一条链把$y$连到树里面去，记$lca(x, y) = z$，

对照上面的图，发现贡献$res = dis(y, rt) - dis(z, rt) = (dis(y,rt) - dis(x, rt) + dis(x, y)) / 2$。

时间复杂度$O(Tn^{2})$。

Code：

#include <cstdio>
#include <cstring>
using namespace std;

const int N = 55;
const int inf = 1 << 30;

int n, d[N][N];

inline void read(int &X) {
    X = 0; char ch = 0; int op = 1;
    for(; ch > '9' || ch < '0'; ch = getchar())
        if(ch == '-') op = -1;
    for(; ch >= '0' && ch <= '9'; ch = getchar())
        X = (X << 3) + (X << 1) + ch - 48;
    X *= op;
}

inline void chkMin(int &x, int y) {
    if(y < x) x = y;
}

int main() {
    for(; ; ) {
        read(n);
        if(n == 0) break;
        for(int i = 1; i <= n; i++)
            for(int j = i + 1; j <= n; j++)
                read(d[i][j]), d[j][i] = d[i][j];
                
        int ans = d[1][2];
        for(int i = 3; i <= n; i++) {
            int res = inf;
            for(int j = 1; j < i; j++)
                chkMin(res, (d[1][i] - d[1][j] + d[i][j]) / 2);
            ans += res;
        }
        printf("%d\n", ans);
    }
    return 0;
}