FFT笔记

打开了政治书又合上了。

学考爆炸预定。

趁着自己还能记得一点东西稍微做一下笔记，要不然又会跟联赛前一样忘得一干二净。

attack大佬的blog

复数

定义$i^2 = -1$，那么所有复数可以表示成$a + bi$的形式（$a, b$为实数）。

在复平面中，$x$轴代表实数，$y$轴（除了原点外）代表虚数。

那么复数$(a + bi)$可以写成形如$(a, b)$的向量，这样子复数的加减运算就会满足平行四边形法则。

$$(a, b) + (c, d) = (a + c, b + d)$$

$$(a, b) - (c, d) = (a - c, b - d)$$

而乘法运算稍微有一些不一样

$$(a, b)*(c, d) = (a + bi) * (c + di) = ac + i * (bc + ad) + bd*i^2 = (ac - bd) + (bc + ad) * i$$

几何意义：模长相乘，幅角相加。

单位根

在负平面上画一个单位圆，然后把这个圆像这样平均分成$n$份（$n$是$2$的幂次）（盗图系列）：

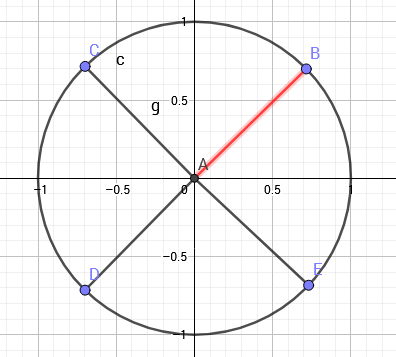
此图中$n = 8$，我们就把向量$AB$（幅角最小而且为正的第一个向量）表示的复数记为单位根$\omega_n$。

抄一段：以圆点为起点，圆的$n$等分点为终点，做$n$个向量，设幅角为正且最小的向量对应的复数为$\omega_n$，称为$n$次单位根。

按照复数运算的法则，剩下的$n - 1$个被划分出来的向量为$\omega_n^2$、$\omega_n^3$、$\omega_n^4$ … $\omega_n^n$。

显然有$\omega_n^0 = \omega_n^n = 0$。

单位根的计算方法涉及到欧拉公式：

$$\omega_n^k = \cos\frac{2\pi k}{n} + i\sin\frac{2\pi k}{n}$$

单位根的美妙性质

$$\omega_{2n}^{2k} = \omega_n^k$$

$$\omega_{n}^{k + \frac{n}{2}} = -\omega_n^k$$

证明可以看图$yy$或者代欧拉公式。

令$S(n) = \sum_{i = 0}^{n - 1}(\omega_n^k)^i$，代入等比数列求和公式

$$S(n) = \frac{(\omega_n^k)^n - 1}{\omega_n^k - 1} = \frac{(\omega_n^n)^k - 1}{\omega_n^k - 1} = \frac{0}{\omega_n^k - 1}$$

发现当$k = n$的时候，这个式子失去意义，但是这时候显然有$S(n) = n$，其他时候$S(n) = 0$。

多项式乘法

假设我们有了多项式$A(x) = \sum_{i = 0}^{n}a_i * x^i$、$B(x) = \sum_{i = 0}^{m}b_i * x^i$（这种表示方法被称为系数表示法），现在我们要计算$A * B$，那么我们会得到一个项数为$n + m + 1$的多项式$C(x)$，但是这样子是$O(n^2)$的时间复杂度。为了更好地计算多项式乘法，我们引入了点值表示法。

把一个多项式看作$n$次函数，这个函数可以由$n + 1$个点确定出来，但是只要得到了两个多项式的点值表示法，我们可以$O(n)$地计算这两个多项式的乘积。

那么$FFT$优化多项式乘法的步骤就有了：系数表示法 --- 点值表示法 --- 无脑乘起来 --- 点值表示法 --- 系数表示法。 

由于单位根的美妙性质，我们把单位根的幂次代入点值的横坐标计算纵坐标。

DFT

这是一个把多项式从系数表示法转化到点值表示法的过程。

用$A(x)$表示一个$n - 1$次的多项式，那么它可以被$n$个点唯一确定。

$$A(x) = \sum_{i = 0}^{n - 1}a_i * x^i$$

按照$i$的奇偶分类，记

$$A_1(x) = a_0 + a_2 * x + \dots + a_{n - 2} * x^{\frac{n}{2} - 1}$$

$$A_2(x) = a_1 + a_3 * x + \dots + a_{n - 1} * x^{\frac{n}{2} - 1}$$

有$A(x) = A_1(x^2) + x * A_2(x^2)$。

代入$\omega_n^{k}$（$k < \frac{n}{2}$）

$$A(\omega_n^{k}) = A_1(\omega_{\frac{n}{2}}^{k}) + \omega_{n}^{k}A_2(\omega_{\frac{n}{2}}^{k})$$

代入$\omega_n^{k + \frac{n}{2}}$

$$A(\omega_n^{k + \frac{n}{2}}) = A_1(\omega_{\frac{n}{2}}^{k}) - \omega_{n}^{k}A_2(\omega_{\frac{n}{2}}^{k})$$

这时候发现了这两个式子在一趟循环中可以一起算出来，如果我们已经算出了一半答案的值，只要从$0$到$\frac{n}{2} - 1$枚举$k$就可以算出另一半，这样子问题的规模就减少了一半。我们递归求解，可以把时间复杂度降到优秀的$O(nlogn)$。

IDFT

这是一个把多项式的从点值表示法转化到系数表示法的过程。

并不是很清楚为什么要这样子做，但是先记着。

假设有多项式$a_i$是多项式$A(x)$的系数，$y_i$表示我们DFT之后得到的点值表示，那么我们把原来得到的$y_i$看作系数，代入$\omega_n^{-k}$，假设我们重新代入之后的值表示为$b_k$，有

$$b_k = \sum_{i = 0}^{n - 1}y_i * (\omega_n^{-k})^i = \sum_{i = 0}^{n - 1}(\sum_{j = 0}^{n - 1}a_j * (\omega_n^i)^j)*(\omega_n^{-k})^i = \sum_{i = 0}^{n - 1}\sum_{j = 0}^{n - 1}a_j * (\omega_{n}^{j - k})^i = \sum_{j = 0}^{n - 1}a_j\sum_{i = 0}^{n - 1}(\omega_{n}^{j - k})^i = n * a_k$$

最后一步代入之前的$S(n)$的公式。

这样子把$k$变成$-k$再做一遍就解决了。

一些优化

然而递归调用了太多空间，这样子还是太慢了。

能不能迭代来实现呢？

思考按照下标的奇偶分类的过程，会得到这样子的结果（盗图 * 2）

 

我们发现按照这样子变换完之后的序列其实就是把下标的二进制表示翻转了一下，我们可以$O(n)$地去递推它。

$$pos_i = (pos_{i >> 1} >> 1) | ((i \& 1) << (l - 1))$$

其中$l$表示序列长度$2^k$次的那个$k$。

背一背这个公式。

这样子我们找到了最后的序列就可以模拟递归的过程实现了。

大大提高了效率。

板

丢个板背背

#include <cstdio>
#include <cmath>
using namespace std;
typedef double db;

const int N = 3e5 + 5;
const db Pi = acos(-1);

int n, m, pos[N], lim = 1;

struct Cpx {
    db x, y;

    inline Cpx(db _x = 0, db _y = 0) {
        x = _x, y = _y;
    }

    friend Cpx operator + (const Cpx u, const Cpx v) {
        return Cpx(u.x + v.x, u.y + v.y);
    }

    friend Cpx operator - (const Cpx u, const Cpx v) {
        return Cpx(u.x - v.x, u.y - v.y);
    }

    friend Cpx operator * (const Cpx u, const Cpx v) {
        return Cpx(u.x * v.x - u.y * v.y, u.x * v.y + u.y * v.x);
    }

} a[N], b[N];

template <typename T>
inline void swap(T &x, T &y) {
    T t = x; x = y; y = t;
}

inline void fft(Cpx *c, int opt) {
    for (int i = 0; i < lim; i++)
        if (i < pos[i]) swap(c[i], c[pos[i]]);
    for (int i = 1; i < lim; i <<= 1) {
        Cpx wn(cos(Pi / i), opt * sin(Pi / i));
        for (int len = i << 1, j = 0; j < lim; j += len) {
            Cpx w(1, 0);
            for (int k = 0; k < i; k++, w = w * wn) {
                Cpx x = c[j + k], y = w * c[j + k + i];
                c[j + k] = x + y, c[j + k + i] = x - y;
            }
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i <= n; i++) scanf("%lf", &a[i].x), a[i].y = 0;
    for (int i = 0; i <= m; i++) scanf("%lf", &b[i].x), b[i].y = 0;

    int l = 0;
    for (; lim <= n + m; lim <<= 1, ++l);
    for (int i = 0; i < lim; i++) pos[i] = (pos[i >> 1] >> 1) | ((i & 1) << (l - 1));

    fft(a, 1), fft(b, 1);
    for (int i = 0; i < lim; i++) a[i] = a[i] * b[i];
    fft(a, -1);

    for (int i = 0; i <= n + m; i++) 
        printf("%d%c", int(a[i].x / lim + 0.5), i == n + m ? '\n' : ' ');

    return 0;
}