物理数学强基基础

标题的意思是这一部分虽然是数学内容，但是解决物理强基问题的过程中可能会用到，所以做一些学习了解。

一.偏导

1.偏导基础

首先根据导数我们知道 \(f'(x)=\lim\limits_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\) 或者说 \(f'(x)=\dfrac{df(x)}{dx}=\dfrac{d}{dx}f(x)\)

个人理解，偏导类似于主元的思想，将不需要求导的未知数视为常数，于是我们记 \(\dfrac{\partial f}{\partial x}=\lim\limits_{\Delta x\to0}\dfrac{S(x+\Delta x,y)-S(x,y)}{\Delta x}\) ，也可以记作 \(\partial_xf=\dfrac{\partial f(x,y)}{\partial x}=\dfrac{\partial}{\partial x}f(x,y)\) ，求解偏导的过程与求导本质上没有区别，运算法则规律等等都适用。

下面来看几个例子

例1：求 \(F(x,y)=\cos (x^2+y^2)\) 的偏导

解： 直接根据偏导的定义： \(\dfrac{\partial F}{\partial x}=-2xsin(x^2+y^2)\)

​ 同理可得：\(\dfrac{\partial F}{\partial y}=-2ysin(x^2+y^2)\)

例2：求 \(F(x,y)=x^y\) 的偏导

**解： ** 直接根据偏导的定义： \(\dfrac{\partial F}{\partial x}=yx^{y-1}\)

​ 同理可得： \(\dfrac{\partial F}{\partial y}=x^y\cdot\ln x\)

2.偏导应用

偏导可以用来求解物理中的平衡点，也叫做函数的稳定值，对应到数学中可以用来求一个多项式的极值

我们直接来看一个例子来理解

例1：求 \(F(x,y)=x^2+y^2\) 的平衡点（稳定值）

解：

首先直接进行偏导可得： \(\dfrac{\partial F}{\partial x}=2x\) ，\(\dfrac{\partial F}{\partial y}=2y\)

\(F(x,y)\) 是一个二元函数，放在三维坐标系中稳定点一定意味着这个点的切平面是一个水平面

偏导的逻辑就是当我们对 \(x\) 进行偏导的时候认为 \(y\) 是不变的，所以一个二维曲面会退化成一个一维曲线，而固定一个参数不变，即假设 \(y\) 不变，则相当于偏导求出来的是 \(xOz\) 这个平面中的抛物线的导数，而如果一个点是稳定点，无论在哪个维度看都会是最小值

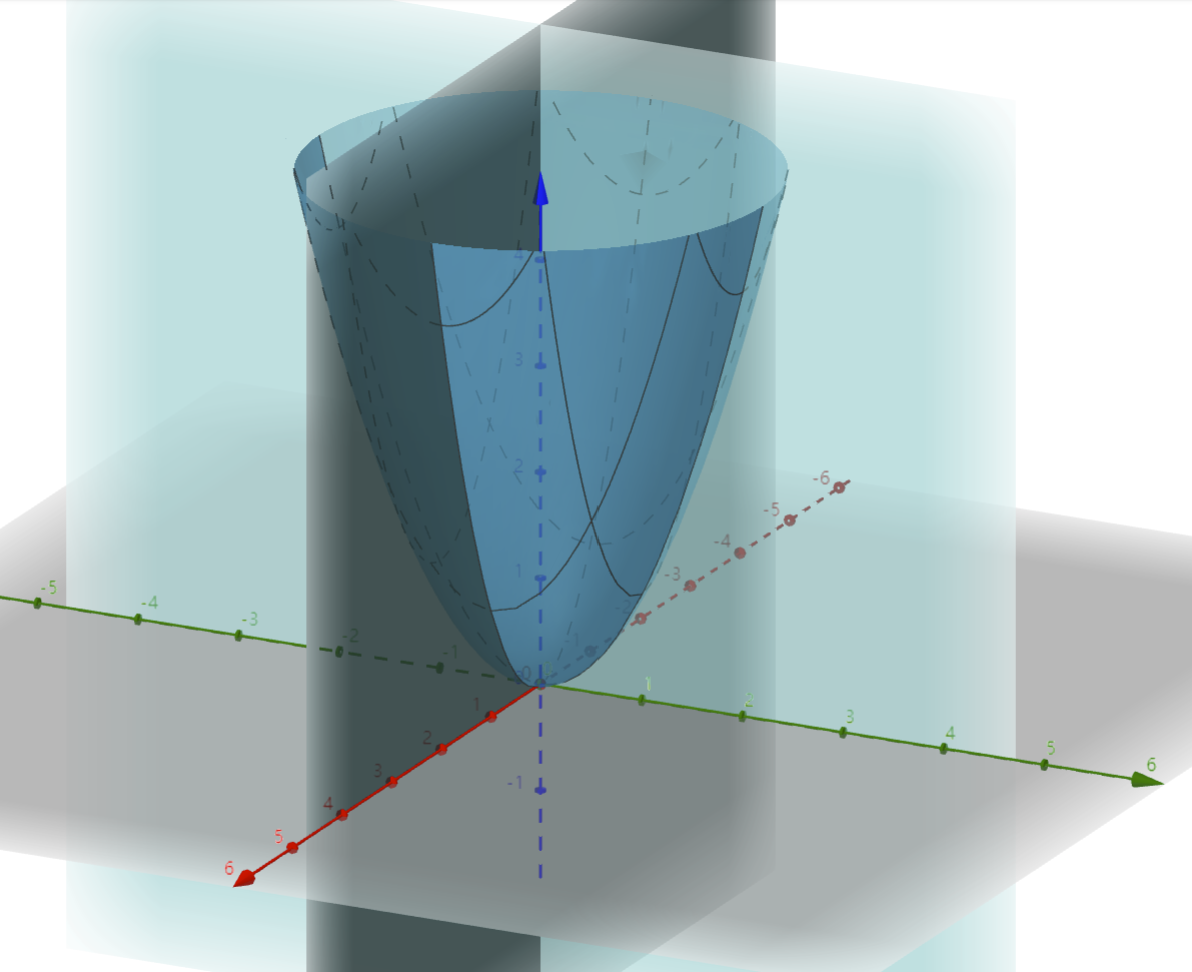
所以直接令 \(\begin{cases}2x=0\\2y=0\\\end{cases}\) ， 这样解得 \(\begin{cases}x=0\\y=0\\\end{cases}\) ，所以我们就知道 \((0,0)\) 就是这个函数的稳定点。

这里需要注意的是如果函数的极值点存在，则稳定点一定位于极值点上，但是稳定点不一定是极值点。

例2：求 \(F(x,y)=x^2+xy+y^2+2x+y+2\) 的稳定点

解：

根据我们上面所知道的，还是直接偏导： \(\dfrac{\partial F}{\partial x}=2x+y+2\) ，\(\dfrac{\partial F}{\partial y}=2y+x+1\)

直接让这两个式子右边都等于 \(0\) 解方程组，即 \(\begin{cases}2x+y+2=0\\2y+x+1=0\\\end{cases}\)

最后可以解得 \(\begin{cases}x=-1\\y=0\\\end{cases}\) ，于是这个函数的稳定点就是 \((-1,0)\)

然而实际中我们遇到的求函数最值也好，求稳定点也好，可能不会这么直白的给一个函数，而是会有对于 \(x\) 和 \(y\) 的限制，举个例子来看。

例3：求 \(F(x,y)=x^2+y^2\) 的平衡点（稳定值），且 \(x,y\) 满足 \(x+y=5\)

分析：我们暂且不讨论不等式或者代入消元等做法。我们发现这个时候不能再简单的令偏导数等于 \(0\) 了，原因就是 \(x+y=5\) 不一定过我的稳定点，所以该如何求解这样的条件极值呢？这个时候就要引出我们的拉格朗日乘数法则。

二.拉格朗日乘数法

真正的拉格朗日乘数法是严格证明出来的，而我们接下来要说的重新构造函数的方法是为了便于理解拉格朗日乘数法使用的规律。

对于上个模块提出的问题

例1：求 \(F(x,y)=x^2+y^2\) 的平衡点（稳定值），且 \(x,y\) 满足 \(x+y=5\)

解：

我们先将条件转化为 \(x+y-5=0\)

然后构造一个目标函数：\(x^2+y^2+\lambda(x+y-5)\)，我们发现这样构造并没有改变原先函数的性质

接下来对目标函数中的 \(x,y,\lambda\) 求偏导，得到： \(\dfrac{\partial F}{\partial x}=2x+\lambda\) ， \(\dfrac{\partial F}{\partial y}=2y+\lambda\) ， \(\dfrac{\partial F}{\partial \lambda}=x+y-5\)

同我们上面所说，解三元一次方程组\(\begin{cases}2x+\lambda=0\\2y+\lambda=0\\x+y-5=0\\\end{cases}\) ，很容易解得\(\begin{cases}x=\dfrac{5}{2}\\y=\dfrac{5}{2}\\\end{cases}\)

所以在有条件的限制下，这个函数的稳定点就是 \((\dfrac{5}{2},\dfrac{5}{2})\)

然而拉格朗日乘数法并不是只能解决限定条件只有一个的问题，对于多个限定条件的情况个数 \(s\) ，只需要设 \(s\) 个参数 \(\lambda_i\) ，按照同样的方法构造目标函数，再求偏导求解即可。

接下来我们看一个实际一些的例子

例2：造一个有底无顶的圆柱形水桶，保持体积一定的时候表面积最小，问圆柱的高与底面半径的比例应为多少

解：

首先先写出我们需要求的表面积的式子 \(S=\pi r^2+2\pi r h\) （注意是有盖无顶）

为了后面偏导方便我们写成 \(F(r,h)=\pi r^2+2\pi r h\)

已知体积一定，所以 \(V=\pi r^2h\) 一定，写成 \(\pi r^2h-V=0\)

构造目标函数 \(I(r,h,\lambda)=\pi r^2+2\pi rh+\lambda(\pi r^2h-V)\)

对于新的函数求偏导列方程组可得， \(\begin{cases}\dfrac{\partial I}{\partial r}=2\pi r+2\pi h+2\pi \lambda rh=0\\\dfrac{\partial I}{\partial h}=2\pi r+\lambda \pi r^2=0\\\dfrac{\partial I}{\partial \lambda}=\pi r^2h-V=0\\\end{cases}\)

可以解得，当 \(r=h\) 时表面积最小，所以 \(\dfrac{h}{r}=1\) 。

三.小量展开

1.泰勒展开基础

我们不加证明的给出如下公式：如果某个函数 \(n\) 阶可导，

则 \(f(x+\Delta x)=f(x)+f'(x)\Delta x+\dfrac{1}{2!}f''(x)\Delta x^2+\dfrac{1}{3!}f^{(3)}(x)\Delta x^3+...+\dfrac{1}{n!}f^{(n)}(x)\Delta x^n+O(n+1)\)

或者将 \(f(x)\) 在 \(x=x_0\) 处的展开记为 \(f(x)=\dfrac{f(x_0)}{0!}+\dfrac{f'(x_0)}{1!}(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f^{(3)}(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x)\) ，其中，\(R_n(x)=\dfrac{f^{(n+1)} (\varepsilon) }{(n+1)!}(x-x_0)^{n+1}\) 被称为 \(n\) 阶泰勒余项

这个公式我们就是泰勒公式。

在实际做题中比较常用的就是要利用泰勒公式在 \(x=0\) 处将 \(f(x)\) 展开，我们以 \(f(x)=e^x\) 为例，在 \(x=0\) 附近展开的意思我们可以理解为，用别的函数去拟合 \(e^x\) 在 \(x=0\) 附近的图像，我们用来拟合的这个函数是没有固定形式的。但是不能发现如果能把这个函数 \(f(x)\) 写成 \(f(x)=a_0+a_1x+a_2x^2+a_3x^3+...\) 我们就可以通过调整 \(a_i\) 的值来拟合出目标函数。于是对于将一个函数展开的问题，就转化为了求解 \(a_i\) 的问题。

接下来我们尝试推导一下 \(f(x)\) 在 \(x=0\) 附近的展开公式： \(f(x)=f(0)+\dfrac{1}{1!}f'(0)x+\dfrac{1}{2!}f''(0)x^2+...+\dfrac{1}{n!}f^{(n)}(0)x^n+...\)

发现 \(a_0\) 比较好求，直接将 \(x=0\) 代入，得到 \(a_0=f(0)\)

求 \(a_1\) 的话我们希望再代入 \(x=0\) ，发现可以直接两边求导 \(f'(x)=a_1+2a_2x+3a_3x^2+...\) ，得到 \(a_1=f'(0)\)

再写一项试试， \(f''(x)=2a_2+6a_3x+12a_4x^2+...\) ，代入 \(x=0\) ，得到 \(a_2=\dfrac{1}{2}f''(0)\)

同理可得 \(a_3=\dfrac{1}{6}f^{(3)}(0)\) ，我们发现对于 \(a_n\) ， \(f^{(n)}(0)\) 的系数实际上就是 \(n!\)

于是 \(a_n\) 是不是就已经呼之欲出了 ：\(a_n=\dfrac{1}{n!}f^{(n)}(0)\) ，其中 \(f^{(n)}(x)\) 表示 \(f(x)\) 在 \(x\) 处的 \(n\) 阶导。

于是我们就拿到了\(f(x)\) 在 \(x=0\) 附近的展开公式。对比一下泰勒展开的完整的公式，其实就是我们令 \(x=0,\Delta x=x\) 就可以拿到我们刚才所推出来的公式。

下面我们就来实践应用一下这个公式

例1：求 \(f(x)=e^x\) 在 \(x=0\) 附近的泰勒展开

解：

\(e^x\) 是一个非常友好的函数，无论求多少次导它永远是它本身，而 \(e^0=1\)

可以直接写出 \(e^x=1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3+\dfrac{1}{4!}x^4+...\)

同时我们发现一个有意思的事情，我们知道 \(e^x\) 的导数是它自己，

对等式两边同时求导，得到 \((e^x)'=0+1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3+...\) ，即等式右边的导数也是它本身。

所以我们就可以说等式右边无限地写下去的函数就是 \(e^x\) ，但是有限的项数则永远不等于 \(e^x\) ，只能是一种拟合的关系，或者简单理解为近似。

配合下面的一组图可以更直观的理解

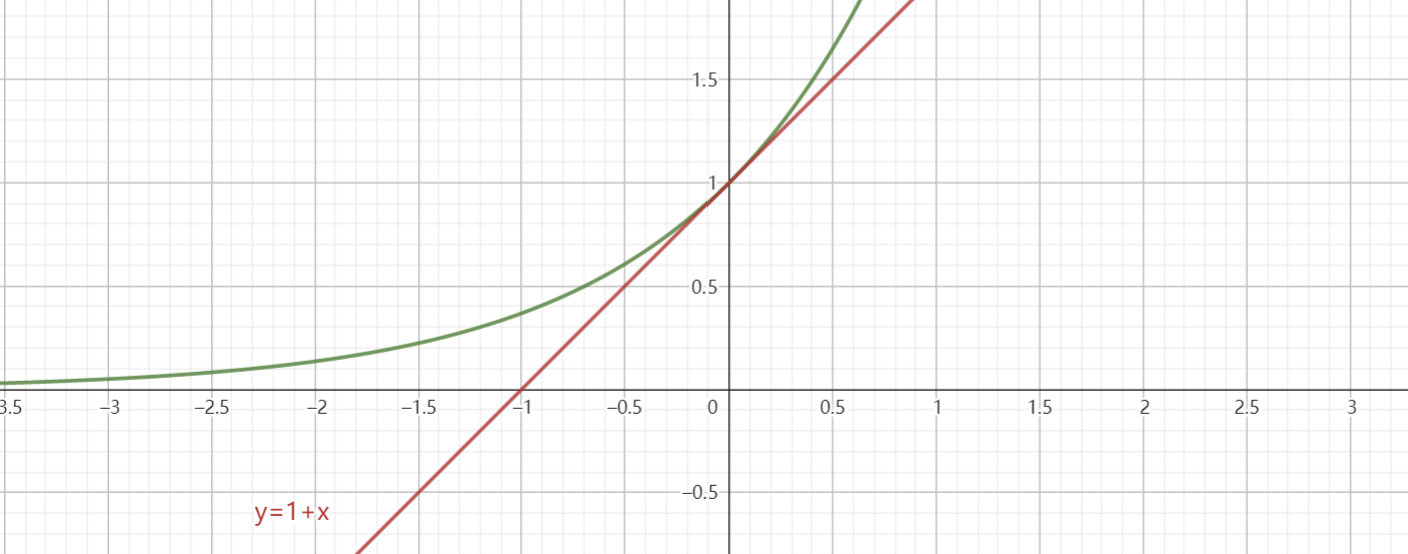
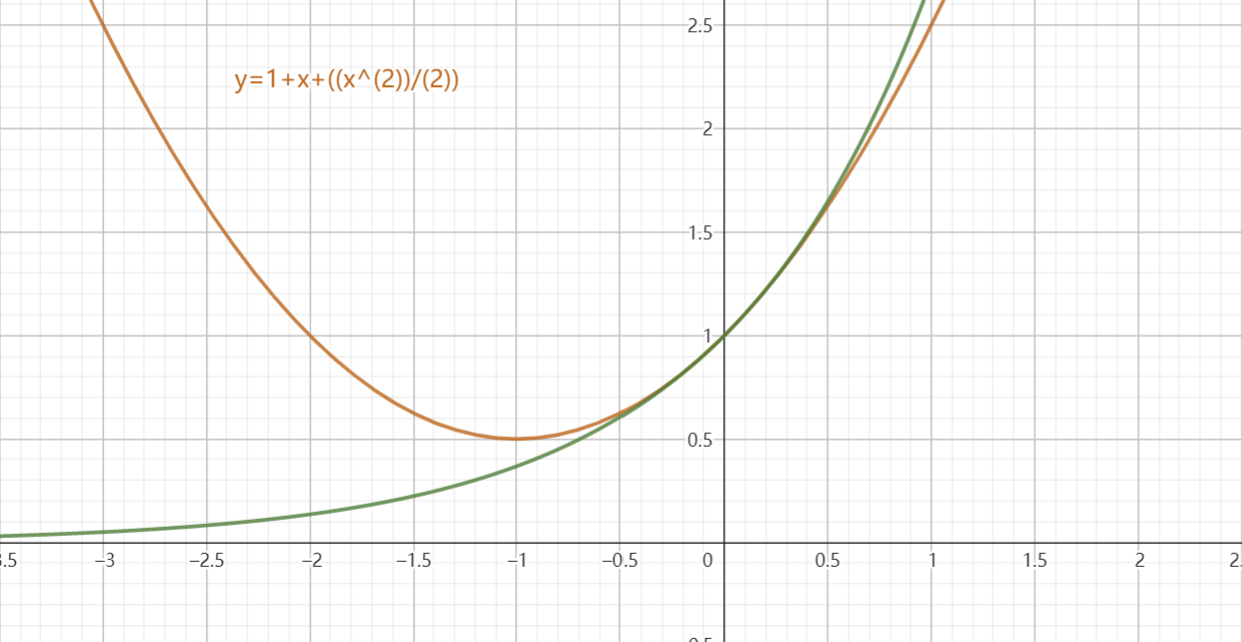
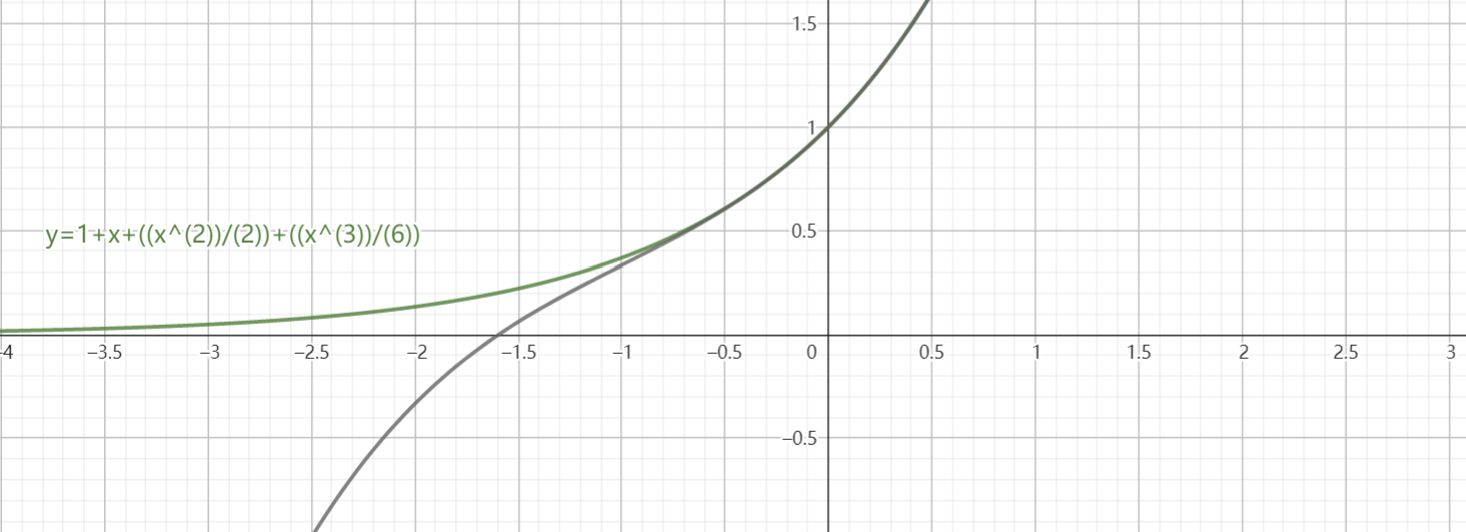
明显看到在 \(n=3\) 时这个图像就已经极其贴近于原函数的图像。

例2：求 \(f(x)=\sin x\) 在 \(x=0\) 附近的泰勒展开， \(O(n)\) 表示忽略 \(n\) 阶以上的无穷小量

解：

直接按照泰勒公式展开即可，得到 \(f(x)=0+\dfrac{1}{1!}\cos(0)x-\dfrac{1}{2!}\sin(0)x^2-\dfrac{1}{3!}\cos(0)x^3+\dfrac{1}{4!}\sin(0)x^4\)

化简一下，得到 \(\sin x=x-\dfrac{x^3}{6}+O(5)\)

想一想：为什么 \(\sin x\) 展开以后只含奇数项？

原因： \(\sin x\) 是一个奇函数，展开后函数的性质并不变

例3：求 \(f(x)=\cos x\) 在 \(x=0\) 附近的泰勒展开， \(O(n)\) 表示忽略 \(n\) 阶以上的无穷小量

直接按照泰勒公式展开即可，得到 \(f(x)=1-\dfrac{1}{1!}\sin(0)x-\dfrac{1}{2!}\cos(0)x^2-\dfrac{1}{3!}\sin(0)x^3+\dfrac{1}{4!}\cos(0)x^4\)

化简一下，可以写成 \(\cos x=1-\dfrac{x^2}{2}+O(4)\)

想一想：为什么 \(\cos x\) 展开以后只含偶数项？

原因： \(\cos x\) 是一个偶函数，展开后函数的性质并不变

例4：求 \(\lim\limits_{x\to0}\dfrac{1-\cos x}{x^2}\)

解：

正常求解的方法肯定是一眼洛必达

但是我们已经学会了泰勒展开，直接 \(\cos x=1-\dfrac{x^2}{2}\) 代入可得答案是 \(\dfrac{1}{2}\)

例5：求 \(\lim\limits_{x\to0}\dfrac{e^x-1-x}{x^2}\)

解：

正常求解的方法还是一眼洛必达，而且需要两次洛必达。

但是我们已经学会了泰勒展开，直接 \(e^x=1+x+\dfrac{1}{2}x^2\) 代入可得，答案是 \(\dfrac{1}{2}\)

总结发现这样做确实也不麻烦，但请一定注意使用条件是 \(x\to0\) ！

2.欧拉公式

观察一下 \(1\) 中的例2与例3中的结果

总感觉可以将 \(\sin x\) 与 \(\cos x\) 交叉在一起可以写成一个公式，但是比较头疼的是正负号问题

再仔细观察一下符号，正正负负，正正负负的循环，发现我们只需要引入一个 \(i\)

接下来对我们已经获得的展开式进行改造

\(e^x=1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3+\dfrac{1}{4!}x^4+...\) 直接还原让新的 \(x\) 变为 \(ix\)

所以 \(e^{ix}=1+\dfrac{1}{1!}ix+\dfrac{1}{2!}(ix)^2+\dfrac{1}{3!}(ix)^3+\dfrac{1}{4!}(ix)^4=1+\dfrac{1}{1!}ix-\dfrac{1}{2!}x^2-\dfrac{1}{3!}ix^3+\dfrac{1}{4!}x^4+...\)

再跟我们已经展开的 \(\sin x\) 和 \(\cos x\) 比对一下

\(\sin x=x-\dfrac{x^3}{6}+O(5)\) ，\(\cos x=1-\dfrac{x^2}{2}+O(4)\)

现在我们已经解决了正负号的问题，但是好像 \(e^{ix}\) 的展开式中有很多带 \(i\) 的式子

仔细观察不难发现，带 \(i\) 的好像都是 \(\sin x\) 的展开项

于是我们就拿到 \(e^{ix}=i\sin x+\cos x\) ，也就是著名的欧拉公式 \(e^{i\theta}=i\sin \theta+\cos\theta\)

ps：现在终于知道为什么学而思的钟表上一点钟给的公式是 \(-e^{i\pi}\) 了

（会一直学习一直更新）