抛物线光学性质证明
接上一篇证明了椭圆的光学性质,今天继续尝试用多种方法证明抛物线的光学性质。**抛物线的光学性质可以理解为:从焦点发射出的光线经抛物线反射后一定平行于抛物线的对称轴**
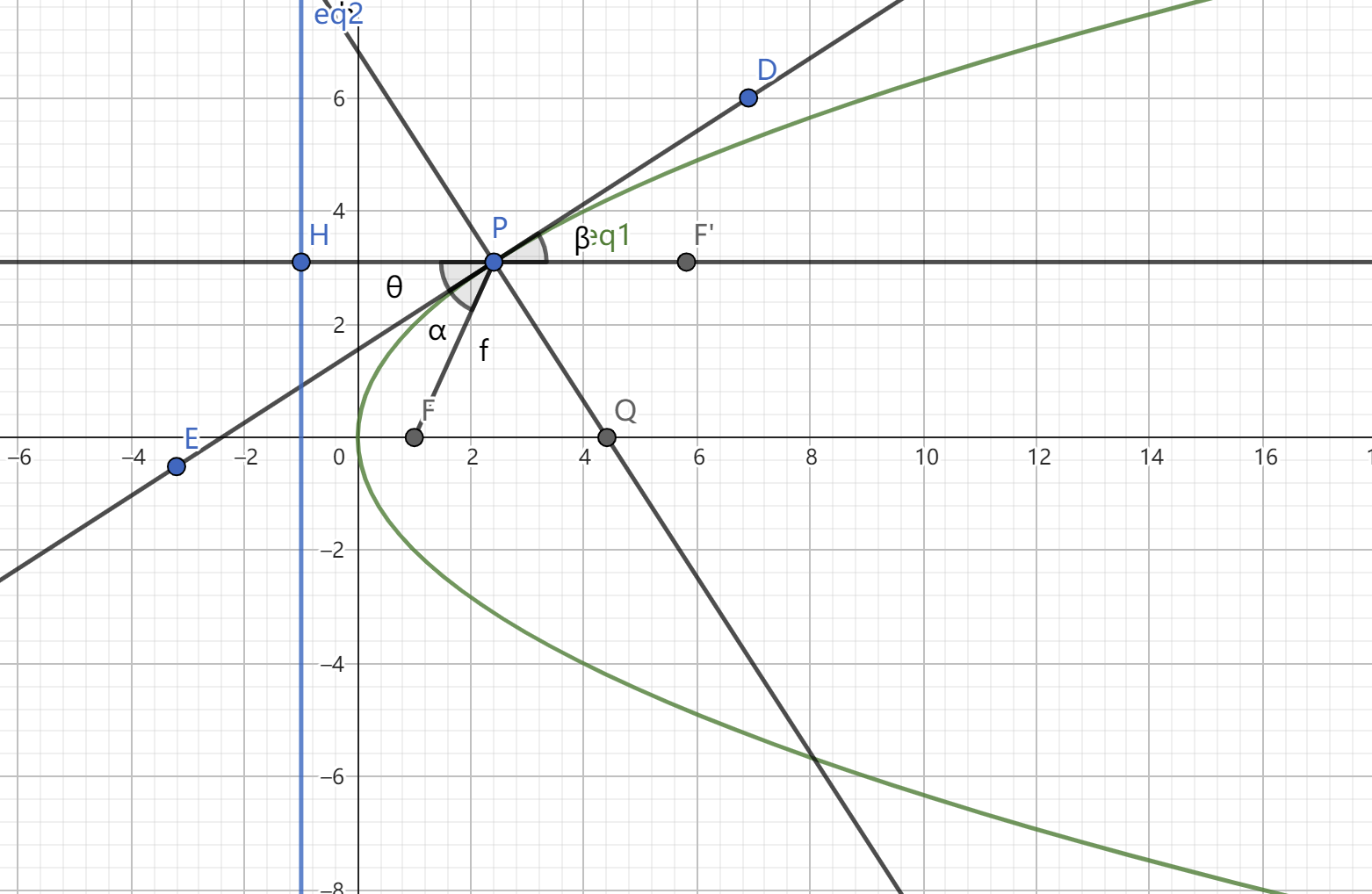
设抛物线 $C:y^2=2px$
其中, $P(x_0,y_0)$ 为抛物线上任意一点 , $l$ 为过 $P$ 关于抛物线的切线 ,$F(\dfrac{p}{2},0)$ 为抛物线的焦点。直线 $PQ$ 为 $l$ 的垂线
经查阅资料发现,在证明抛物线的光学性质过程中,常常将命题转化,转化为已知 $PF'$ 平行于 $x$ 轴 ,去证明 $\alpha=\beta$
证法一:平行平分出等腰
我们发现如果 $\alpha=\beta$ ,那么它们各自的余角相等,又由 $PF'$ 平行于 $x$ 轴可得 $PF=FQ$ ,所以我们只要证明 $PF=FQ$ ,就可以证明抛物线的光学性质。
根据抛物线的性质 $PF=PH$ $\therefore PF=x_0+\dfrac{p}{2}$
先由 $P$ 点的切线即为点 $P$ 关于 $C$ 的极线,再利用垂直,
表示 $l_{PQ}:y-y_0=-\dfrac{y_0}{p}(x-x_0)$
将 $y=0$ 代入拿到 $Q(x_0+p,0)$
于是 $|FQ|=|OQ|-|OF|=x_0+p-\dfrac{p}{2}=x_0+\dfrac{p}{2}$
不难得到 $|FQ|=|FP|$
综上,抛物线光学性质得证。
证法二:到角公式
要证明角相等,在斜率均已知的情况下,可以直接使用到角公式
焦点 $F$ 的坐标为 $(\dfrac{p}{2},0)$ $\therefore$ 直线 $PF$ 的斜率 $k_{PF}=\dfrac{y_0}{x_0-\dfrac{p}{2}}$
进而垂线 $PQ$ 的斜率 $k_{PQ}=-\dfrac{y_0}{p}$
由 $PF'$ 平行于 $x$ 轴可知 $k_{PF'}=0$
于是表示 $\tan \angle QPF=\dfrac{k_{PQ}-k_{PF}}{1+k_{PQ}k_{PF}}=-\dfrac{-\dfrac{y_0}{p}-\dfrac{y_0}{x_0-\dfrac{p}{2}}}{1-\dfrac{y_0}{p}\cdot \dfrac{y_0}{x_0-\dfrac{p}{2}}}=-\dfrac{y_0(x_0+\dfrac{p}{2})}{p(x_0-\dfrac{p}{2})-y_0^2}$
又$\because y_0^2=2px_0$ ,代入上式得,$\tan \angle QPF=\dfrac{y_0(x_0+\dfrac{p}{2})}{p(x_0+\dfrac{p}{2})}=\dfrac{y_0}{p}$
再表示 $\tan \angle QPF'=\dfrac{k_{PF'}-k_{PQ}}{1+k_{PF'}k_{PQ}}=\dfrac{y_0}{p}$
于是得到 $\tan \angle QPF=\tan \angle QPF'$ $\therefore \angle QPF=\angle QPF'$
综上,抛物线的光学性质得证。
证法三:证明中垂线
我们发现有对顶角 $\theta=\beta$ ,所以证明 $\alpha=\beta$ 可以转化为 $\theta=\beta$ ,而如果 $l$ 为 $HF$ 的中垂线,则抛物线的光学性质得证。
有 $F(\dfrac{p}{2},0),H(-\dfrac{p}{2},y_0)$
可得 $k_{FH}=-\dfrac{y_0}{p}$
根据极点极线可得, $l:y_0y=2p\cdot \dfrac{x_0+x}{2}=px+px_0$
于是 $k_l=\dfrac{p}{y_0}$ 且 $k_l\cdot k_{FH}=-1$ 即 $FH$ 垂直于 $l$
设 $FH$ 的中点为 $N(0,\dfrac{y_0}{2})$ ,将 $x=0$ 代入 $l$ 得,$y=\dfrac{px_0}{y_0}$
又$\because y_0^2=2px_0 \therefore p=\dfrac{y_0^2}{2x_0}$
将 $p$ 回代可得到, $y=\dfrac{\dfrac{y_0^2}{2x_0}\cdot x_0}{y_0}=\dfrac{y_0}{2}$
于是可得 $FH$ 的中点在 $l$ 上,所以 $l$ 为 $FH$ 的中垂线
综上,抛物线的光学性质得证。
总结来说抛物线中光学性质的证明相比来说,比椭圆的光学性质证明起来相对容易,证法一和证法三利用极点极线相关知识可以大量简便计算,并且都应用了一定的几何知识,使解析几何的计算量减少,而证法二到角公式就是纯粹的解析几何的证明方式。


