椭圆光学性质证明
终于可以借项目式作业的机会，完成当时圆锥曲线结论整理里一笔带过的光学性质证明，本篇主要给出椭圆光学性质的三种证明方法。
首先我们假设椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
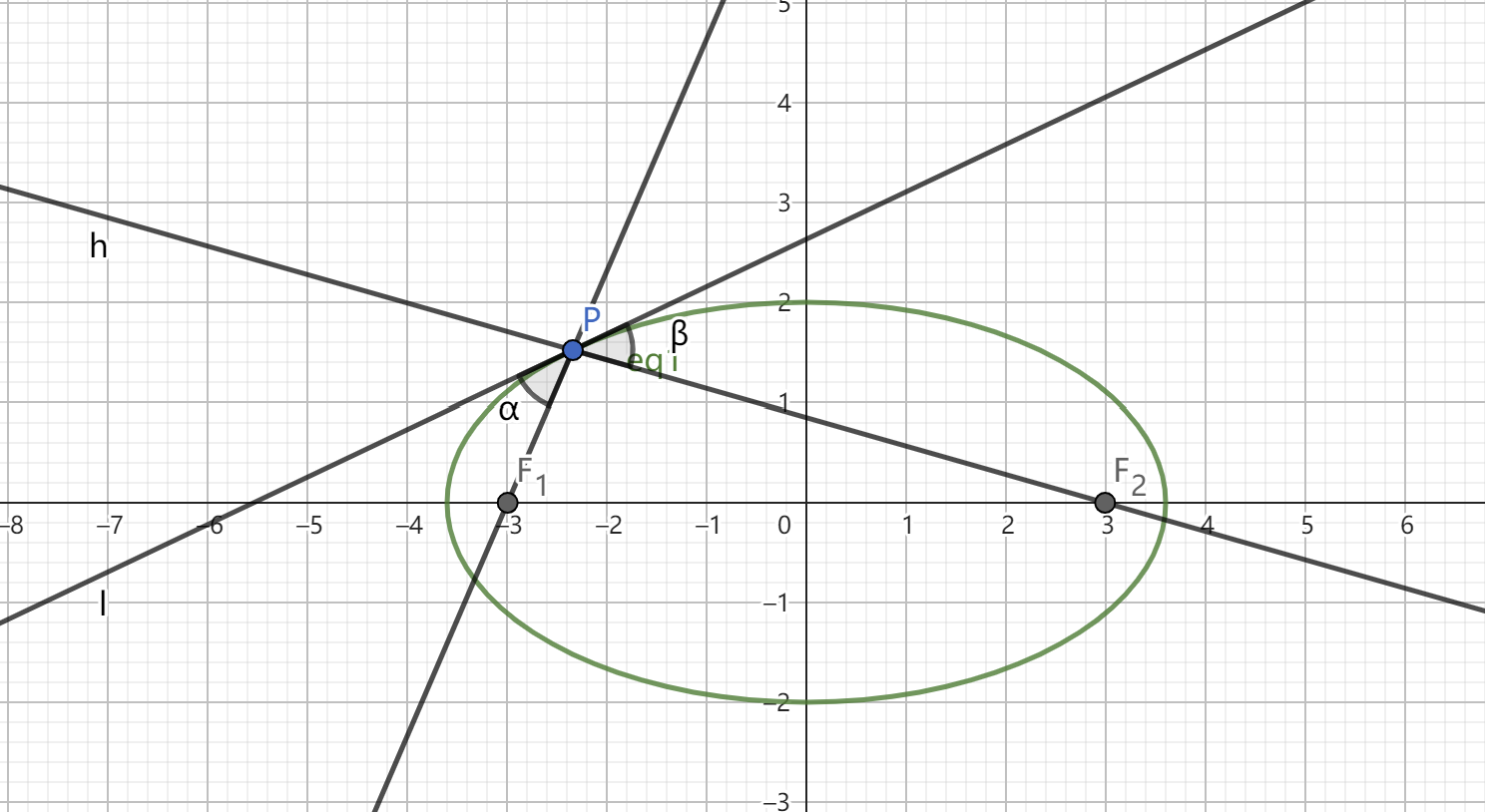
其中，$p(x_0,y_0)$ 为椭圆上任意一点，$F_1(-c,0)$与 $F_2(c,0)$ 为椭圆的左右焦点，$l$ 为过 $p$ 点关于椭圆的切线，$\alpha$ 为 $l$ 到 $PF_1$ 的角，$\beta$ 为 $PF_2$ 到 $l$ 的角， **椭圆的光学性质简单理解为：从一个焦点射出的一条光线经椭圆反射后一定经过另一焦点**
证法一：到角公式表达正切值
首先我们将命题转化，转化为已知直线 $PF_1$ 与 $PF_2$ ，去证明 $\alpha=\beta$ 。
假设 $l$ 的斜率存在，$P$ 处的切线即为该点关于椭圆的极线
可知 $l:b^2x_0x+a^2y_0y=a^2b^2$ 所以 $l$ 的斜率 $k=-\dfrac{b^2x_0}{a^2y_0}$
则 $\tan \alpha =\dfrac{\dfrac{y_0}{x_0+c}+\dfrac{b^2x_0}{a^2y_0}}{1-\dfrac{y_0}{x_0+c}\cdot\dfrac{b^2x_0}{a^2y_0}}=\dfrac{a^2b^2+b^2cx_0}{c^2x_0y_0+a^2cy_0}=\dfrac{b^2}{cy_0}$
则 $\tan \beta =\dfrac{-\dfrac{y_0}{x_0-c}-\dfrac{b^2x_0}{a^2y_0}}{1+\dfrac{y_0}{x_0-c}\cdot(-\dfrac{b^2x_0}{a^2y_0})}=\dfrac{a^2b^2-b^2cx_0}{a^2cy_0-c^2x_0y_0}=\dfrac{b^2}{cy_0}$
从而 $\tan \alpha=\tan \beta$
于是我们就证明了 $\alpha=\beta$
当 $l$ 的斜率不存在时， $l$ 即为 $x$ 轴，满足 $\alpha=\beta$
综上，椭圆的光学性质得证。
证法二：角平分线定理
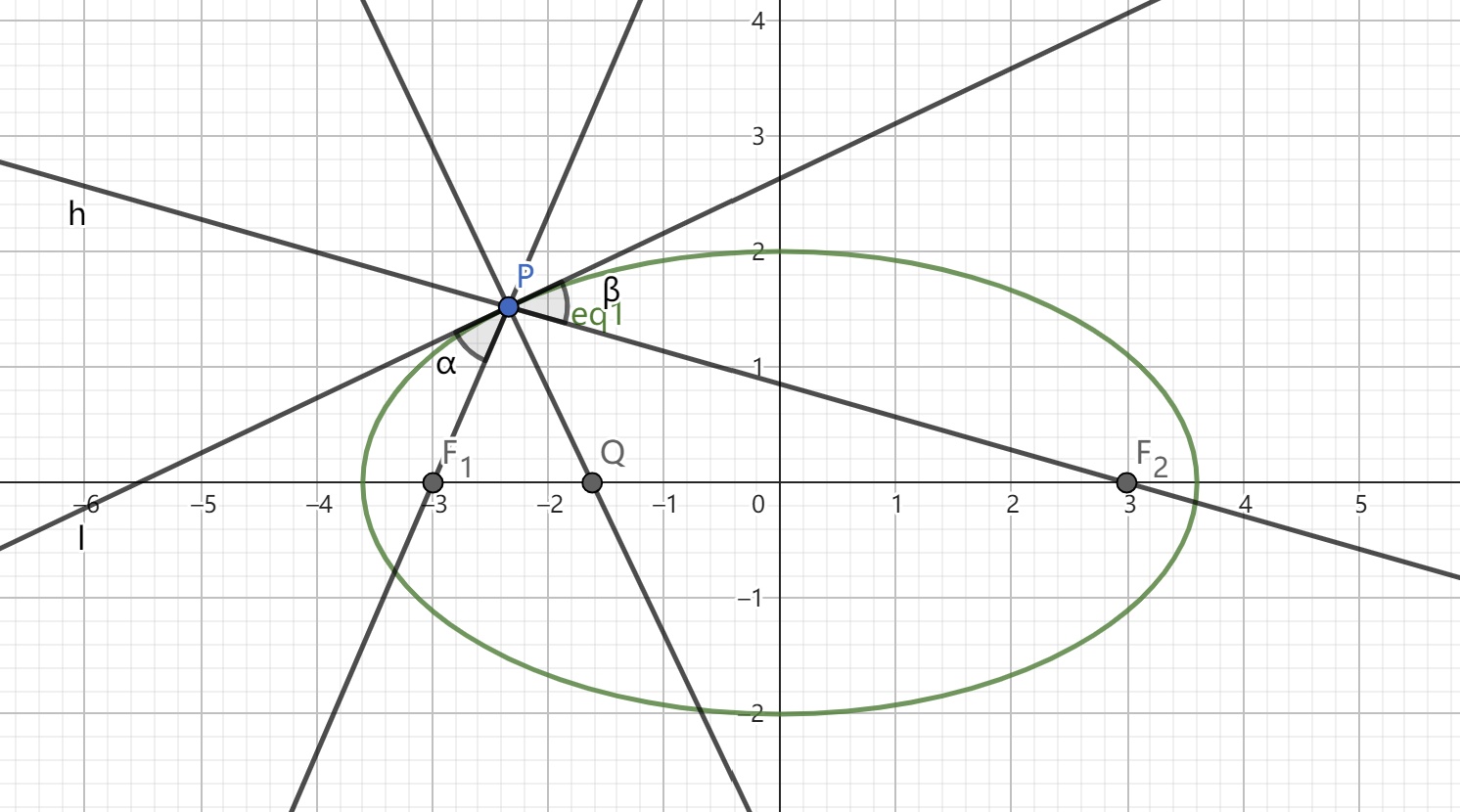
观察发现，过点 $p$ 做 $l$ 的垂线 $l'$ 发现欲证明 $\alpha=\beta$ 可以去证明它们各自的余角相等，进而想到角平分线，进而想到角平分线定理。（已经讨论过 $l$ 的斜率不存在时的情况，故接下来的几种证法不再考虑 $l$ 的斜率不存在时的情况）
由证法一可知，$l$ 的斜率 $k=-\dfrac{b^2x_0}{a^2y_0}$ ，于是可知 $k_{PQ}=\dfrac{a^2y_0}{b^2x_0}$
于是可以写出 $l_{PQ}:y-y_0=\dfrac{a^2y_0}{b^2x_0}(x-x_0)$ ，
进而拿到 $Q(x_0-\dfrac{b^2}{a^2}x_0,0)=(\dfrac{c^2x_0}{a_2},0)$
表示 $QF_1$ 与$QF_2$ 长度：$|QF_1|=\dfrac{c^2x_0}{a^2}+c$ ，$|QF_1|=c-\dfrac{c^2x_0}{a^2}$
$\dfrac{|QF_1|}{|QF_2|}=\dfrac{a^2+cx_0}{a^2-cx_0}=\dfrac{a+ex_0}{a-ex_0}$
这时我们发现 $|PF_1|=a+ex_0$ ，$|PF_2|=a-ex_0$
于是就有 $\dfrac{|PF_1|}{PF_2}=\dfrac{a+ex_0}{a-ex_0}=\dfrac{|QF_1|}{|QF_2|}$
这个时候根据角平分线定理我们就有 $\angle F_1PQ=\angle F_2PQ$
进而 $\alpha=\beta$
综上，椭圆的光学性质得证。
证法三：构造对称，三点共线
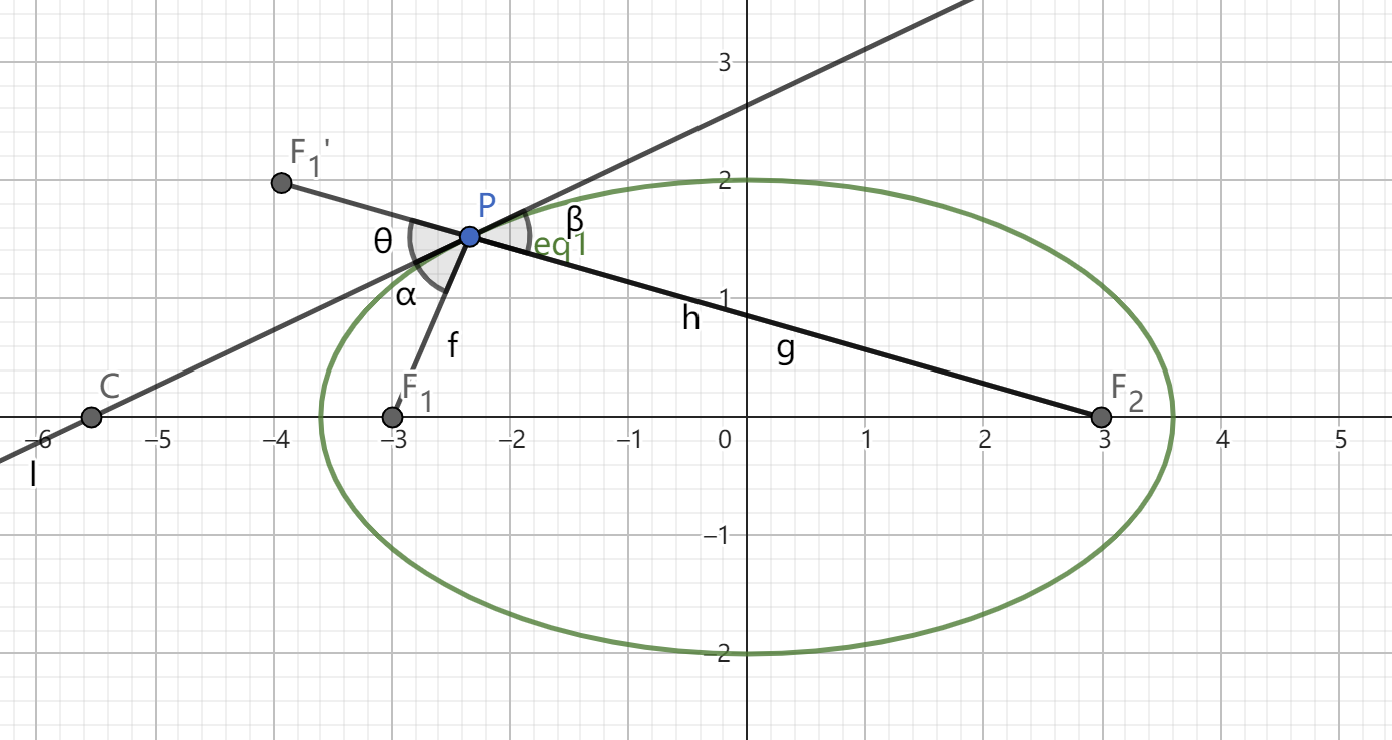
构造对称的思路是我们发现对称后有 $\alpha=\theta$ 所以只要证明 $\theta=\beta$ 即可证明椭圆的光学性质，而当 $F_1',P,F_2$ 三点共线时 $\theta$ 与 $\beta$ 为该直线的一组对顶角。然而这种方法的缺点是没有很好的方法来计算对称点 $F_1'$ 的坐标，只能硬算，比较锻炼计算能力。
由 $l$ 是 $C$ 的极线可知 ，$l:\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$
设 $F_1'(m,n)$，由对称可知 $\begin{cases}\dfrac{n}{m+c}=\dfrac{a^2y_0}{b^2x_0}\\\dfrac{\dfrac{m-c}{2} \cdot x_0}{a^2}+\dfrac{\dfrac{n}{2} \cdot y_0}{b^2}=1\end{cases}$
解得，$\begin{cases}m=\dfrac{2a^2b^4x_0+b^4x_0^2c-a^4y_0^2c}{a^4y_0^2+b^4x_0^2}\\n=\dfrac{2a^2b^4y_0(a^2+cx_0)}{a^4y_0^2+b^4x_0^2}\end{cases}$
于是 $k_{F_1'F_2}=\dfrac{n}{m-c}$ ，计算发现 $k_{F_1'F_2}=\dfrac{n}{m-c}=\dfrac{y_0}{x_0-c}$
于是得到 $F_1',P,F_2$ 三点共线， 所以$ \alpha=\beta$
综上椭圆的光学性质得证。
以上就是本文给出的光学性质的三种证明方法，都是从解析几何的角度入手，可以发现利用角平分线定理可以优化计算的过程，而使用对称则会面临很复杂的计算，正常的到角公式相对来说难度中等。
