KMP&exKMP

（之前学的一些东西都没打笔记，给忘的差不多了。从这个开始要记得写笔记了。）

注意事项：所有的字符串的下标从1开始。

KMP

对于一个字符串 s ，定义它的前缀数组a,其中a[i]表示子串s[1...i]前缀与后缀相同的最大长度（不包括串自身）。

对于朴素的算法，自然是n^2的暴力。考虑利用前面位置的值来计算当前位置的值。

设当前位置为i。发现a[i]<=a[i-1]+1，同时发现当s[i]=s[a[i-1]+1]时，a[i]=a[i-1]+1。

那么如果不相等呢？

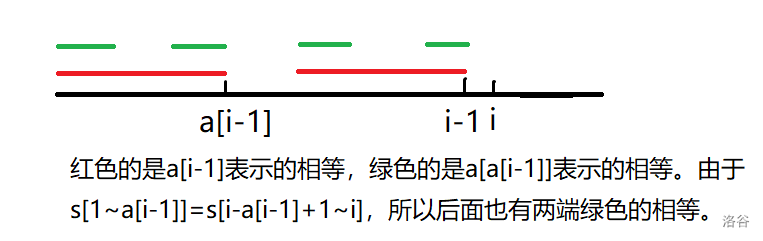
我们需要找到一个更小的j，考虑j的取值可能在哪里。我们需要找到一段满足s[i-j+1...i]=s[1...j]的，才能快速得出当前答案。

发现a[a[i-1]]的值满足这一性质（参考下图）。所以我们可以不断递归，直至j=0。（要注意，j=0时有可能a[i]=1。）

用途：

我们处理出来这个数组有什么用呢？

首先当然是匹配。假设当前有一个串S，一个模式P，求P在S的哪些位置能匹配？

我们将两个字符串连接起来：P+‘#’+S（‘#’表示一个在两个串中都不出现的字符）。然后计算出 |P|+2~|P|+|S|+1 的前缀数组。根据前缀数组的性质，当 a[i]=|P| 时，P在S中出现了一个匹配。

计算一个串中，本质不同的串的数量。

考虑每次加入一个字符，计算产生了多少个不同的串。从末尾加入一个字符，然后设当前串的反串为S'。处理出每个位置的前缀数组。整个序列的前缀数组的最大值即为增加的本质相同的串。

计算每个前缀的出现次数。

容易，计算有多少个前缀数组的值是相同的就行了。

exKMP

exKMP，也叫 Z 函数。定义字符串S的Z函数为：z[i]表示字符串S与以i开头的后缀的LCP。

考虑字符串中常用的处理方法：利用前面已经求得的数据计算当前的数据。

我们维护一个l、r，表示与S的某个前缀相同的、右端点最右的区间，其实就是S[i...i+z[i]]。这里我们钦定z[1]=0，从第2个数开始计算。

设当前的位置为i。当i<r时，由于S[i...r]=S[i-l+1...r-l+1]，所以考虑通过z[i-l+1]求z[i]。若z[i-l+1]<r-i+1,则z[i]=z[i-l+1]。因为如果z[i]>z[i-l+1]，那么根据l与r的定义，S[z[i-l+1]+1]=S[i-l+1+1]，即z[i-l+1]会更大。若z[i-l+1]≥r-i+1，那么我们将z[i]暂时设为r-i+1,然后暴力延伸。

当i≥r时，将z[i]设为0，然后暴力延伸。记得计算完一个z[i]后，要更新l、r。

考虑时间复杂度的正确性。每一次延伸，如果没有暴力延伸，则时间复杂度为O(1)；如果暴力延伸，则r一定会改变，又由于r最大为n，所以最多扩展|S|位。总的复杂度为O（|S|）。

应用：

同KMP一样，可以匹配，可以计算本质不同的子串数量。

计算一个串的最小整周期，即对于一个串S，求一个长度最小的串t，使得t可以通过若干次复制构成S。算出位置i的z[i]后，若i-1为n的因数且z[i]+i-1=|S|，则S[1...i-1]为S的整周期。