BZOJ3211花神游历各国-线段树&树状数组-(HDU4027同类型)
(有任何问题欢迎留言或私聊 && 欢迎交流讨论哦
题意:BZOJ HDU
原题目描述在最下面。
两种操作,1:把区间的数字开方一次,2:区间求和。
思路:
线段树:
显然不能暴力单点更新。但是有一个规律就是一个数再开方log次后就会变成1了。变成1就没有开方的必要了。
所以用lazy==1表示此区间内数字全都小于等于1,无需更新。
对于lazy==0单点更新,lazy==1的不更新。
求和就是普通的区间求和。看下push_up()函数即可。
树状数组:
树状数组区间求和很方便。然后这题的开发更操作只需要修改一下add函数即可。每次add(\(i, \sqrt{ ar_{i} - ar_{i}}\))。
当然也不是暴力枚举更新。有些点的值小于等于1就没必要更新。这是用一个并查集维护一下每个位置下一个需要更新的位置在哪里就可以了。
####AC代码: BZOJ3211线段树
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <algorithm>
#include <set>
#include<assert.h>
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) (x)&(-(x))
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int N = (int)1e5+7;
const int mod = 10007;
int n, q;
struct lp{
int l,r;
LL delta;
int lazy;
}cw[N<<2];
LL ar[N];
//lazy==1表示全部小于等于1
void push_up(int rt){
cw[rt].delta=cw[lson].delta+cw[rson].delta;
cw[rt].lazy=(cw[lson].lazy&cw[rson].lazy);
}
void build(int l,int r,int rt){
int mid = (l+r)>>1;
cw[rt].l=l,cw[rt].r=r;
cw[rt].lazy=0;
if(l==r){
cw[rt].delta=ar[l];
if(ar[l]<=1)cw[rt].lazy=1;
return;
}
build(l,mid,lson);build(mid+1,r,rson);
push_up(rt);
}
void update(int L,int R,int rt){
int l=cw[rt].l,r=cw[rt].r,mid=(l+r)>>1;
if(l==r){
cw[rt].delta=(LL)sqrt(cw[rt].delta*1.0);
if(cw[rt].delta<=1)cw[rt].lazy=1;
return;
}
if(L<=mid&&cw[lson].lazy==0)update(L,R,lson);
if(R>mid&&cw[rson].lazy==0)update(L,R,rson);
push_up(rt);
}
LL query(int L,int R,int rt){
int l=cw[rt].l,r=cw[rt].r,mid=(l+r)>>1;
if(L<=l&&r<=R){
return cw[rt].delta;
}
LL sum = 0;
if(L>mid)sum = query(L,R,rson);
else if(R<=mid)sum = query(L,R,lson);
else {
sum = query(L,R,lson)+query(L,R,rson);
}
return sum;
}
int main(){
while(~scanf("%d", &n)){
for(int i=1;i<=n;++i){
scanf("%lld",&ar[i]);
}
build(1,n,1);
scanf("%d",&q);
while(q--){
int op,l,r;
scanf("%d%d%d",&op,&l,&r);
if(op==2){
update(l,r,1);
}else{
printf("%lld\n", query(l,r,1));
}
}
}
return 0;
}
BZOJ3211树状数组
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <algorithm>
#include <set>
#include<assert.h>
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) (x)&(-(x))
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int N = (int)1e5+7;
const int mod = 10007;
int n, q;
LL bit[N],ar[N];
int fa[N];
void add(int x,LL z){while(x<=n)bit[x]+=z,x+=lowbit(x);}
LL query(int x){LL sum=0;while(x)sum+=bit[x],x-=lowbit(x);return sum;}
int Fi(int x){
return fa[x]==x?x:fa[x]=Fi(fa[x]);
}
int main(){
while(~scanf("%d", &n)){
memset(bit,0,sizeof(bit));
for(int i=1;i<=n;++i){
scanf("%lld",&ar[i]);
add(i,ar[i]);
}
for(int i=1;i<=n;++i)fa[i]=i;
fa[n+1]=n+1;
scanf("%d",&q);
while(q--){
int op,l,r;
scanf("%d%d%d",&op,&l,&r);
if(op==2){
for(int j=l;j<=r;){
LL tmp = (LL)sqrt(ar[j]);
add(j,tmp-ar[j]);
ar[j]=tmp;
fa[j]=j;
if(tmp<=1)fa[j]=j+1;
j=(Fi(j)==j?j+1:fa[j]);
}
}else{
printf("%lld\n", query(r)-query(l-1));
}
}
}
return 0;
}
HDU4027 ``` #include
####原题目描述: 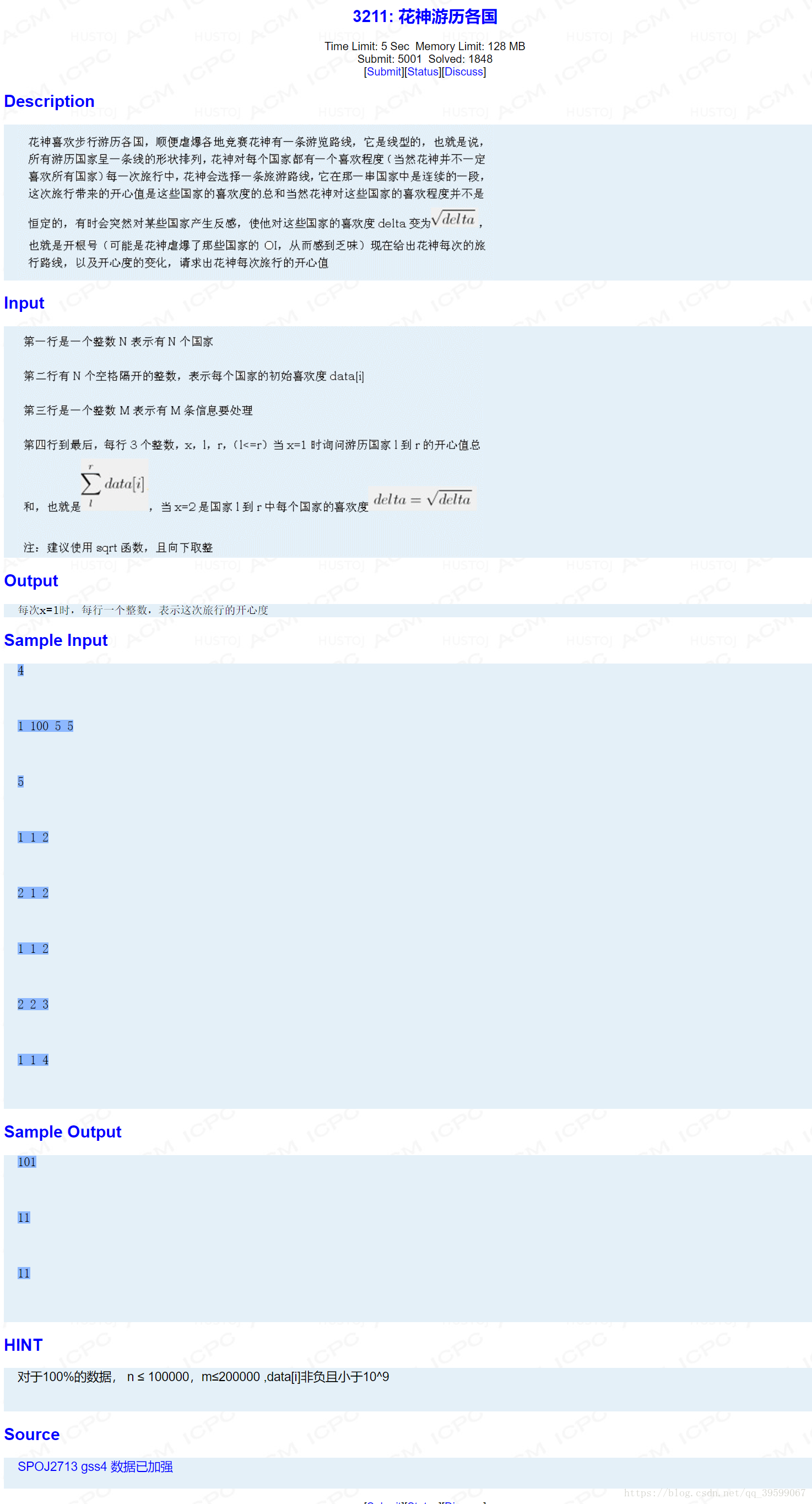
ACMer,无怨无悔



 浙公网安备 33010602011771号
浙公网安备 33010602011771号