hdu6578 2019湖南省赛D题Modulo Nine 经典dp
@
题目

第一题题意是一共有{0,1,2,3}四种数字供选择,问有多少个长度为n的序列满足所有m个条件,每个条件是说区间[L,R]内必须有恰好x个不同的数字。
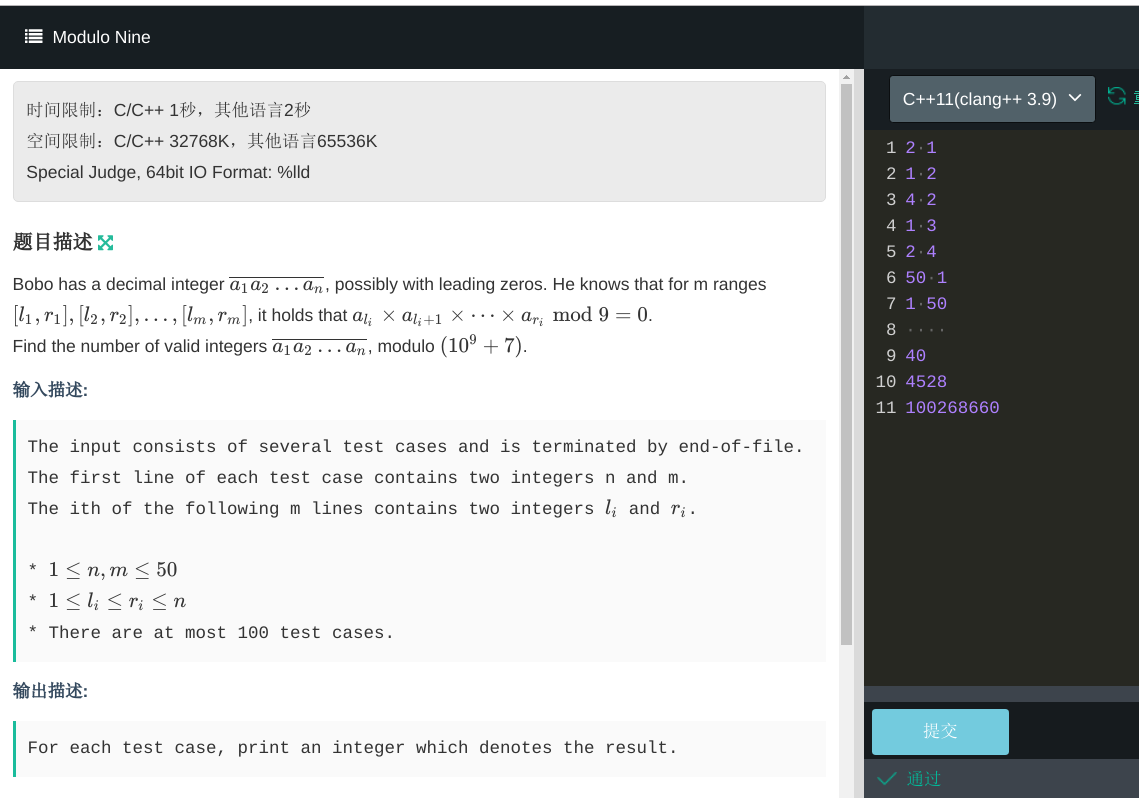
第二题题意是10个数字供选择,问有多少个长度为n的序列满足所有m个条件,每个条件是说区间[L,R]数字的乘积必须是9的倍数。
解析
- hdu6578
- \(dp[t][i][j][k]\)表示填完前\(t\)个位置,{\(0,1,2,3\)}中出现的数字最后一次出现的位置排序后为\(t,i,j,k(t\gt i\gt j\gt k)\)的方案数。\(0\)表示数字未出现。
- 枚举四种转移:
- 填\(t-1\)位置的数字:\(dp[t][i][j][k]\)
- 填\(i\)位置的数字:\(dp[t][t-1][j][k]\)
- 填\(j\)位置的数字:\(dp[t][t-1][i][k]\)
- 填\(k\)位置的数字:\(dp[t][t-1][i][j]\)
- 但是不是所有转移都有效,所以要枚举限制条件,将不合法的转移pass掉
- 枚举所有终点在\(t\)点的限制条件,将不合法的转移的\(dp\)值归零。
- 时间复杂度:\(O(n^4)\),滚动数组优化空间复杂度:\(O(n^3)\)
- 2019湖南省赛D题Modulo Nine
- 关于乘积是否是9的倍数,这里只有3类数字,0和9表示两个3,3和6表示一个3,其他表示零个3
- \(dp[t][i][j]\)表示填完前\(t\)个位置,最后一个3在\(i\),倒数第二个3在\(j\)的方案数。
- 枚举3种转移:
- 填\(0或9\):\(dp[t][t][t]\)
- 填\(3或6\):\(dp[t][t][i]\)
- 填其他数字:\(dp[t][i][j]\)
- 但是不是所有转移都有效,所以要枚举限制条件,将不合法的转移pass掉
- 枚举所有终点在\(t\)点的限制条件,将不合法的转移的\(dp\)值归零。
- 时间复杂度:\(O(n^3)\),滚动数组优化空间复杂度:\(O(n^2)\)
两题思路一模一样,是一种很经典的dp。
AC_Code
hdu6578
const int mod = 998244353;
const int MXN = 1e5 + 7;
const int MXE = 2e5 + 7;
int n, m, c;
vector<pii> mp[MXN];
LL dp[2][101][101][101];
void get_dp() {
dp[c][0][0][0] = 1;
for(int t = 1; t <= n; ++t) {
c ^= 1;
for(int i = 0; i <= t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) dp[c][i][j][k] = 0;
for(int i = 0; i < t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) {
if((i != j && j != k) || k == 0) {
dp[c][i][j][k] = (dp[c][i][j][k] + dp[c ^ 1][i][j][k]) % mod;
dp[c][t - 1][j][k] = (dp[c][t - 1][j][k] + dp[c ^ 1][i][j][k]) % mod;
dp[c][t - 1][i][j] = (dp[c][t - 1][i][j] + dp[c ^ 1][i][j][k]) % mod;
dp[c][t - 1][i][k] = (dp[c][t - 1][i][k] + dp[c ^ 1][i][j][k]) % mod;
}
}
for(int h = 0; h < (int)mp[t].size(); ++h) {
int l = mp[t][h].fi, x = mp[t][h].se;
for(int i = 0; i < t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) {
int cnt = 1;
if(i >= l) ++ cnt;
if(j >= l) ++ cnt;
if(k >= l) ++ cnt;
if(cnt != x) dp[c][i][j][k] = 0;
}
}
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("/home/cwolf9/CLionProjects/ccc/in.txt", "r", stdin);
//freopen("/home/cwolf9/CLionProjects/ccc/out.txt", "w", stdout);
#endif
int tim = read();
while(tim --) {
n = read(), m = read();
for(int i = 1, a, b, c; i <= m; ++i) {
a = read(), b = read(), c = read();
mp[b].eb(mk(a, c));
}
get_dp();
LL ans = 0;
for(int i = 0; i < n; ++i)
for(int j = 0; j <= i; ++j)
for(int k = 0; k <= j; ++k) if((i != j && j != k) || k == 0) ans = (ans + dp[c][i][j][k]) % mod;
printf("%lld\n", (ans+mod)%mod);
for(int i = 0; i <= n; ++i) mp[i].clear();
}
#ifndef ONLINE_JUDGE
cout << "time cost:" << clock() << "ms" << endl;
#endif
return 0;
}
2019省赛D
const int mod = 1e9 + 7;
const int MXN = 1e5 + 7;
const int MXE = 2e5 + 7;
int n, m, c;
int mp[MXN];
LL dp[2][101][101];
void get_dp() {
clr(dp, 0);
dp[c][0][0] = 1;
for(int t = 1; t <= n; ++t) {
c ^= 1;
for(int i = 0; i <= t; ++i) for(int j = 0; j <= i; ++j) dp[c][i][j] = 0;
for(int i = 0; i <= t; ++i) {
for(int j = 0; j <= i; ++j) {
dp[c][i][j] = (dp[c][i][j] + dp[c^1][i][j] * 6) % mod;
dp[c][t][i] = (dp[c][t][i] + dp[c^1][i][j] * 2) % mod;
dp[c][t][t] = (dp[c][t][t] + dp[c^1][i][j] * 2) % mod;
}
}
if(mp[t] == -1) continue;
for(int i = 0; i <= t; ++i) {
for(int j = 0; j <= i; ++j) {
if(i < mp[t] || j < mp[t]) dp[c][i][j] = 0;
}
}
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("/home/cwolf9/CLionProjects/ccc/in.txt", "r", stdin);
//freopen("/home/cwolf9/CLionProjects/ccc/out.txt", "w", stdout);
#endif
int tim = 1;
while(~scanf("%d%d", &n, &m)) {
for(int i = 1; i <= n; ++i) mp[i] = - 1;
for(int i = 1, a, b; i <= m; ++i) {
a = read(), b = read();
mp[b] = big(mp[b], a);
}
get_dp();
LL ans = 0;
for(int i = 0; i <= n; ++i) for(int j = 0; j <= i; ++j) ans = (ans + dp[c][i][j]) % mod;
printf("%lld\n", (ans + mod) % mod);
}
#ifndef ONLINE_JUDGE
cout << "time cost:" << clock() << "ms" << endl;
#endif
return 0;
}
ACMer,无怨无悔



 浙公网安备 33010602011771号
浙公网安备 33010602011771号