记一些数学引理和结论等
@
一些结论
\(gcd(x^a-1,x^b-1)=x^{gcd(a,b)}-1\)
\(gcd(fib[x],fib[y])=fib[gcd(x,y)]\)
费马大定理
定理:\(a^n+b^n=c^n\;\;(n\ge3时没有整数解)\)
扩展:当\(a=2*k+1\)为奇数时,\(c=k^2+(k+1)^2,b=c-1\);当\(a=2*k\)为偶数时,\(c=k^2+1,b=c-2\)。
第二类斯特林数
\(S(n,k)\)一个\(n\)元集的所有\(k\)划分的个数。\(n\)个不同的球放到\(k\)个同样的盒子使无空盒。
定理1:\(S(n+1,k)=S(n,k-1)+k\times S(n,k)\)
定理2:\(S(n,2)=2^{n-1}-1,S(n,n-1)=C_2^n\)
定理3:\(S(n+1,k)=C_{k-1}^nS(k-1,k-1)+C_{k}^nS(k,k-1)+...+C_{n}^nS(n,k-1)\)
整数的无序拆分
\(B(n,k)=0,\;n<k\)
\(B(n,1)=B(n,n)=1\)
\(H(n)=B(n,1)+B(n,2)+...+B(n,n)\)
定理1:\(B(n+k,k)=B(n,1)+B(n,2)+...+B(n,k)\)
- 解法1:记忆化搜索(复杂度接近\(O(n^2)\))
\(dfs(n, m)\) 表示用\(1-m\)的数字无序分解\(n\)的方案数。
1.当\(n==m\)时:你可以选择用\(n\)分解得到\(1\)个方案,加上不用\(n\)分解的方案\(dfs(n,m-1)\)
2.当\(n>m\)时:你可以选择用\(m\)分解得到方案\(dfs(n-m,m)\),加上不用\(m\)分解的方案\(dfs(n,m-1)\)
3.当\(n<m\)时:就等于\(dfs(n,n)\)
当然把记忆化搜索改成递推也很好写,常数可能小点???
const int mod = 1e9 + 7;
const int MXN = 1e4 + 7;
int n;
LL dp[MXN][MXN];
LL dfs(int n, int m) {//用1-m的数字无序分解n的方案数
if(n == 1 || m == 1) return 1;
if(dp[n][m] != -1) return dp[n][m];
LL ans = 0;
if(n == m) ans = dfs(n, m-1) + 1;
if(n < m) ans = dfs(n, n);
if(n > m) ans = dfs(n, m-1) + dfs(n-m, m);
ans %= mod;
dp[n][m] = ans;
return ans;
}
int main(int argc, char const *argv[]){
scanf("%d", &n);
memset(dp, -1, sizeof(dp));
printf("%lld\n", dfs(n, n));
memset(dp, -1, sizeof(dp));
for(int i = 1; i <= n; ++i) dp[i][1] = 1, dp[1][i] = 1;
for(int i = 2; i <= n; ++i) {
for(int j = 2; j <= n; ++j) {
if(i == j) dp[i][j] = (dp[i][j-1] + 1)%mod;
else if(i > j) dp[i][j] = (dp[i][j-1] + dp[i-j][j])%mod;
else dp[i][j] = dp[i][i];
}
}
printf("%lld\n", dp[n][n]);
return 0;
}
- 解法2:母函数法之暴力解多项式乘法
\(G(x)=(x^0+x^1+...+x^n)\times (x^0+x^2+x^4+...+x^{2\times \frac n2})\times ...\times(x^0+x^{n\times \frac nn})\)
用两个数组迭代暴力求解。
母函数法应该还可以优化吧?
const int mod = 1e9 + 7;
const int MXN = 1e5 + 7;
int n;
LL n1[MXN], n2[MXN], v[MXN];
LL a[MXN], b[MXN];
void init(int n) {
for(int i = 1; i <= n; ++i) {
n1[i] = 0; n2[i] = n/i; v[i] = i;
b[i] = 1; a[i] = 0;
}
b[0] = 1;
}
void solve(int n) {
for(int i = 2; i <= n; ++i) {
memcpy(a, b, sizeof(LL)*(n+2));
memset(b, 0, sizeof(LL)*(n+2));
for(int j = n1[i]; j <= n2[i] && j*v[i] <= n; ++j) {
for(int k = 0; k+j*v[i] <= n; ++k) {
b[k+j*v[i]] = (b[k+j*v[i]]+a[k])%mod;
}
}
}
printf("%lld\n", b[n]);
}
int main(int argc, char const *argv[]){
scanf("%d", &n);
init(n);
solve(n);
return 0;
}
再贴一个母函数的暴力模板:
int n;
LL n1[MXN], n2[MXN], v[MXN];
LL a[MXN], b[MXN];
int last;
void init(int n) {
for(int i = 1; i <= n; ++i) {
n1[i] = 0; n2[i] = n/i; v[i] = i;
b[i] = 0; a[i] = 0;
}
b[0] = 1;
last = 0;
}
void solve(int n) {
for(int i = 1; i <= n; ++i) {
int last2 = min((LL)n, last+n2[i]*v[i]);
memcpy(a, b, sizeof(LL)*(last2+2));
memset(b, 0, sizeof(LL)*(last2+2));
for(int j = n1[i]; j <= n2[i] && j*v[i] <= last2; ++j) {
for(int k = 0; k <= last && k+j*v[i] <= last2; ++k) {
b[k+j*v[i]] = (b[k+j*v[i]]+a[k])%mod;
}
}
last = last2;
}
printf("%lld\n", b[n]);
}
int main(int argc, char const *argv[]){
scanf("%d", &n);init(n);solve(n);
return 0;
}
输出无序拆分的解:
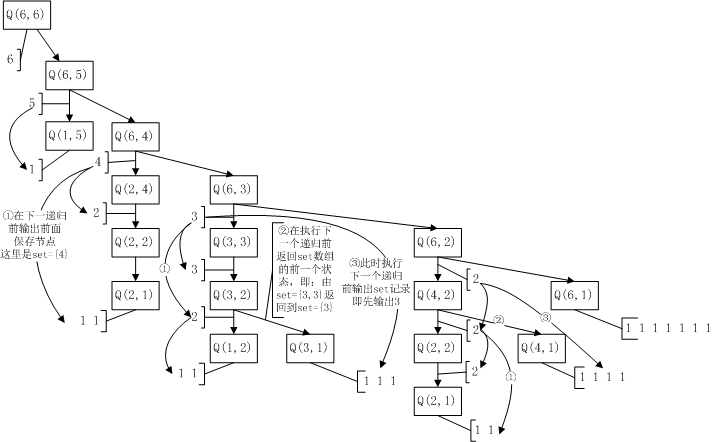
#include <stdio.h>
//使用一个数组记录在递归过程中产生的前面需要重复输出的值
int set[100];
//用于在递归过程中判断是否递归到最深处,输出回车
int k;
//此函数表示使用不大于m的整数对n进行拆分的情况,i用于表示set数组已经存在的记录数长度
void q(int n,int m,int i){
if(n==k&&n!=m){
//此时递归栈已经退回到某一分支的最上层,输出回车
//并重置计数器i为0
printf("\n");
i=0;
}
if(n==1){
//当n为1,意味者着只能表示1
printf("1 ");
return;
}
else if(m==1){
//当m为1,意味着要输出n个m相加
for(int i=0; i<n-1; i++)
printf("1+");
printf("1 ");
return;
}
if(n<m) {
q(n,n,i);
}
if(n==m){
//当n等于m时,到达本次递归求和的一个叶子,此时需要输出多一个空格,表示下一次输出为另一个叶子
printf("%d ",n);
//在递归输出另一个叶子之前,将之前记录的在叶子之上的数一并输出,如上图示过程1
for(int j=0; j<i; j++)
printf("%d+",set[j]);
q(n,m-1,i);
}
if(n>m){
//如果n大于m,使用m作为分解,则要首先输出m+的形式
printf("%d+",m);
//记录下作为树干节点m的值并使i自增
set[i++]=m;
//递归输出m+以后的分解
q(n-m,m,i);
//递归完毕后需要将数组记录后退一个,回到上一个节点,如上图示过程2
i--;
//执行另一个分支,在下一次递归之前输出记录的数据,如上图示过程3
for(int j=0; j<i; j++)
printf("%d+",set[j]);
//递归输出另一分支情况
q(n,m-1,i);
}
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
if(n<=0){
printf("Please input a positive interger.\n\n");
continue;
}
k=n;
q(n,n,0);
printf("\n\n");
}
return 0;
}
伯努利数模板
\(B_0=1,B_1=-\frac 12,B_2=\frac 16,B_3=0,B_4=-\frac 1{30}\)
\(B_5=0,B_6=\frac1{42},B_7=0,B_8=-\frac1{30},B_9=0\)
nlog(n)
//day7 J oeis
//n%4==0和n=1时Bnl[n]是负的
//a(n) = abs[c(2*n-1)] where c(n)= 2^(n+1) * (1-2^(n+1)) * Ber(n+1)/(n+1)
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:1024000000,1024000000")
namespace BNL{
using namespace std;
typedef long long LL;
const int N = 300020;
//const LL P = 50000000001507329LL; //190734863287 * 2 ^ 18 + 1 G = 3 常数巨大
//const int P = 1004535809; //479 * 2 ^ 21 + 1 G = 3
const int P = 998244353; // 119 * 2 ^ 23 + 1 G = 3
//const int P = 104857601; // 25 * 2 ^ 22 + 1 G = 3
//const int P = 167772161; // 5 * 2 ^ 25 + 1 G = 3
const int G = 3;
int wn[25];
LL mul(LL x, LL y) {return (x * y - (LL)(x / (long double)P * y + 1e-3) * P + P) % P;}
int qpow(LL a, int b, int p) {
LL res = 1;
for(;b;b>>=1,a=a*a%p) {
if(b&1) res=res*a%p;
}
return (int)res;
}
void getwn() {
for(int i = 1; i <= 21; ++i) {
int t = 1 << i;
wn[i] = qpow(G, (P - 1) / t, P);
}
}
void change(int *y, int len) {
for(int i = 1, j = len / 2; i < len - 1; ++i) {
if(i < j) swap(y[i], y[j]);
int k = len / 2;
while(j >= k) {
j -= k;k /= 2;
}
j += k;
}
}
void NTT(int *y, int len, int on) {
change(y, len);
int id = 0;
for(int h = 2; h <= len; h <<= 1) {
++id;
for(int j = 0; j < len; j += h) {
int w = 1;
for(int k = j; k < j + h / 2; ++k) {
int u = y[k];
int t = 1LL * y[k+h/2] * w % P;
y[k] = u + t;
if(y[k] >= P) y[k] -= P;
y[k+h/2] = u - t + P;
if(y[k+h/2] >= P) y[k+h/2] -= P;
w = 1LL * w * wn[id] % P;
}
}
}
if(on == -1) {
for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]);
int inv = qpow(len, P - 2, P);
for(int i = 0; i < len; ++i)
y[i] = 1LL * y[i] * inv % P;
}
}
int tmp[N];
void get_inv(int A[], int A0[], int t) {
if(t == 1) {
A0[0] = qpow(A[0], P - 2, P);
return;
}
get_inv(A, A0, t / 2);
for(int i = 0; i < t; ++i) tmp[i] = A[i];
for(int i = t; i < 2 * t; ++i) tmp[i] = 0;
for(int i = t / 2; i < 2 * t; ++i) A0[i] = 0;
NTT(tmp, 2 * t, 1);
NTT(A0, 2 * t, 1);
for(int i = 0; i < 2 * t; ++i) {
tmp[i] = (2 - 1LL * tmp[i] * A0[i] % P) % P;
if(tmp[i] < 0) tmp[i] += P;
A0[i] = 1LL * A0[i] * tmp[i] % P;
}
NTT(A0, 2 * t, -1);
}
int B[N], f[N], nf[N], a[N];
void init() {
f[0] = 1;
for(int i = 1; i < N; ++i) f[i] = 1LL * f[i-1] * i % P;
nf[N-1] = qpow(f[N-1], P - 2, P);
for(int i = N - 2; i >= 0; --i) {
nf[i] = 1LL * nf[i+1] * (i + 1) % P;
}
for(int i = 0; i < N - 1; ++i) a[i] = nf[i+1];
int len = 1 << 17;
get_inv(a, B, len);
for(int i = 0; i < len; ++i) B[i] = 1LL * B[i] * f[i] % P;
}
void solve_bnl() {
getwn();//最前面
init();
}
}
int main() {
BNL::solve_bnl();
printf("%d\n", BNL::B[2]);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
namespace POLY{
const int MAXN = 262144;
const int MOD = 998244353, ROOT = 3;
typedef vector<int> Poly;
inline int add(int a, int b){ return (a + b) % MOD; }
inline int sub(int a, int b){ return (a - b + MOD) % MOD; }
inline int mul(int a, int b){ return (long long)a * b % MOD; }
int power(int a, int b){
int ret = 1;
for (int t = a; b; b >>= 1){
if (b & 1)ret = mul(ret, t);
t = mul(t, t);
}
return ret;
}
int pow2(int n){
int ret = 1;
while (ret < n)ret *= 2;
return ret;
}
void clean(Poly& p){
while (!p.empty() && !p.back())p.pop_back();
}
Poly cut(const Poly& p, int n){
return Poly(p.begin(), p.begin() + n);
}
Poly expand(const Poly& p, int n){
Poly ret(n);
copy(p.begin(), p.end(), ret.begin());
return ret;
}
Poly operator + (Poly p, const Poly& p2){
p.resize(max(p.size(), p2.size()));
for (int i = 0; i < (int)p2.size(); i++)
p[i] = add(p[i], p2[i]);
return p;
}
Poly operator - (Poly p, const Poly& p2){
p.resize(max(p.size(), p2.size()));
for (int i = 0; i < (int)p2.size(); i++)
p[i] = sub(p[i], p2[i]);
return p;
}
Poly operator * (Poly p, int x){
for (int i = 0; i < (int)p.size(); i++)
p[i] = mul(p[i], x);
return p;
}
void dot(Poly& p, const Poly& p2){
for (int i = 0; i < (int)p.size(); i++)
p[i] = mul(p[i], p2[i]);
}
void fft(Poly& a, bool rev){
static int g[MAXN + 1], w[MAXN] ;
if (!g[0]){
w[0] = 1;
g[0] = 1; g[1] = power(ROOT, (MOD - 1) / MAXN);
for (int i = 2; i < MAXN; i++)
g[i] = mul(g[i - 1], g[1]);
}
int len = a.size(), d = MAXN / len;
for (int i = 1, j = len / 2; i < len; i++){
w[i] = g[d * (rev ? len - i : i)];
if (i < j) swap(a[i], a[j]);
for (int k = len; j < k; k >>= 1, j ^= k);
}
for (int s = 1; s < len; s <<= 1){
int step = len / s / 2;
for (int j = 0; j < len; j += 2 * s){
for (int k = j, wk = 0; k < j + s; k++, wk += step){
int t = mul(w[wk], a[k + s]);
a[k + s] = sub(a[k], t); a[k] = add(a[k], t);
}
}
}
if (rev){
int t = MOD / len; t = mul(t, t * len);
for (int i = 0; i < len; i++)
a[i] = mul(a[i], t);
}
}
Poly operator * (const Poly& p1, const Poly& p2){
if (p1.empty() || p2.empty())return Poly();
int len = pow2(p1.size() + p2.size());
Poly p3 = expand(p1, len), p4 = expand(p2, len);
fft(p3, 0); fft(p4, 0);
dot(p3, p4); fft(p3, 1);
p3.resize(p1.size() + p2.size() - 1);
return p3;
}
Poly inv(const Poly& p){
int len = 2 * pow2(p.size());
Poly a, b(len), exa = expand(p, len);
b[0] = power(p[0], MOD - 2);
for (int i = 4; i <= len; i *= 2){
a = cut(exa, i / 2);
a.resize(i); b.resize(i);
fft(a, 0); fft(b, 0); dot(a, b);
dot(b, Poly(i, 2) - a);
fft(b, 1); b.resize(i / 2);
}
b.resize(p.size());
return b;
}
int fact[MAXN], factInv[MAXN];
void init(){
fact[0] = 1;
for (int i = 1; i < MAXN; i++)
fact[i] = mul(fact[i - 1], i);
factInv[MAXN - 1] = power(fact[MAXN - 1], MOD - 2);
for (int i = MAXN - 1; i; i--)
factInv[i - 1] = mul(factInv[i], i);
}
Poly bernoulli(int n){//MAXN是n的至少两倍
Poly p(n + 1);
for (int i = 0; i <= n; i++)
p[i] = factInv[i + 1];
return inv(p);
}
vector<int> Bnl;
const int maxn = 2e5 + 7;
int jie[maxn];
void solve_bnl() {
jie[1] = jie[0] = 1;
for(int i = 2; i < maxn; ++i) jie[i] = 1LL*jie[i-1]*i%MOD;
init();
Bnl = bernoulli(100010);
for(int i = 0; i < 100010; ++i) Bnl[i]=Bnl[i]*1LL*jie[i]%MOD;
}
}
int main() {
POLY::solve_bnl();
printf("%d\n", POLY::Bnl[2]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号