CodeForces 449D(容斥，DP

题目：给出N（<=10^6）个数，每个数<=10^6. 从中选出至少1个数，易知有2^N-1种不同方案。那么在这些方案中，有多少种满足选出的所有数AND起来为0呢？

我是不会做的，找了一个题解然而看了好久看不懂，后来看了下官方题解发现我看得那个有个地方写错了。。。。

官方题解如下：

Firstly, we can use inclusion-exclusion principle in this problem. Let f(x) be the count of number i where A_i&x = x. Let g(x) be the number of 1 in the binary respresentation of x. Then the answer equals to .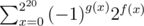

Now the task is to calculate f(x) for every integer x between 0 and 2²⁰. Let f_k(x) be the count of number i where Y₀&X₀ = X₀ and X₁ = Y₁ (they are defined below).

We divide x and A_i into two parts, the first k binary bits and the other 20 - k binary bits. Let X₀ be the first part of x and X₁ be the second part of x. Let Y₀ be the first part of A_i and Y₁ be the second part of A_i.

We can calculate f_k(x) in O(1):

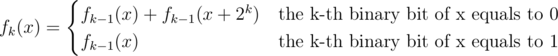
The problem can be solved in O(n * 2ⁿ) now (n = 20 in this problem).

做的时候作死把pow函数里的乘数写成了int。。。。总是犯这种错误。。。我发誓以后不用ｉｎｔ做数学题了。。。。然后，对于这个ｄｐ的思路究竟是咋想出来的还是没有啥头绪，估计下次碰到这种提还是不会吧。。。每次都能看懂题解然后下次又不会了啊。。。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<functional>
#include<queue>
using namespace std;
typedef long long ll;
const int maxv=1e5+30;
const ll mod=1000000007;
int N;
int a[1<<20];
int dp[22][1<<20];
int fpow(int x,ll p){
    int ans=1;
    ll xx=x;
    while(p>0){
        if(p&1)
        ans=(xx*ans)%mod;
        xx=(xx*xx)%mod;
        p>>=1;
    }
    return ans;
}
void add(int &a,int b){
    a=((a+b)%mod+mod)%mod;
}
int main(){
    ///freopen("in","r",stdin);
    cin>>N;
    for(int i=0;i<N;i++) scanf("%d",&a[i]);
    sort(a,a+N);
    for(int i=0;i<N;i++){
        if(a[i]&1) add(dp[0][a[i]],1),add(dp[0][a[i]-1],1);
        else add(dp[0][a[i]],1);
    }
    for(int i=1;i<20;i++){
        for(int j=1;j<(1<<20);j++){
            if(j&(1<<i)) add(dp[i][j],dp[i-1][j]);
            else add(dp[i][j],dp[i-1][j]),add(dp[i][j],dp[i-1][j+(1<<i)]);
        }
    }
    int ans=fpow(2,N)-1;
        for(int j=1;j<(1<<20);j++){
            int bb=__builtin_popcount(j);
            if(bb%2) add(ans,-fpow(2,dp[19][j])+1);
            else add(ans,fpow(2,dp[19][j])-1);
        }
    cout<<ans<<endl;
    return 0;
}