贝叶斯网络——概率图模型之有向图

目录

• 图模型
• 贝叶斯网络
• 条件独立的三种情况
  • • 第一种情况tail-to-tail
    • 第二种情况tail-to-head
    • 第三种情况head-to-head
• D-seperation
• 贝叶斯网络模型

图模型

图模型是用图的方式表示概率推理 ，将概率模型可视化，方便展示变量之间的关系，概率图分为有向图和无向图。有向图主要是贝叶斯网络，无向图主要是马尔科夫随机场。

贝叶斯网络

为了理解有向图对于描述概率分布的作⽤，⾸先考虑三个变量\(a, b, c\)上的⼀个任意的联合分布\(p(a, b, c)\)。通过使⽤概率的乘积规则，我们可以将联合概率分布写成如下形式:

\[p(a,b,c)=p(c|a,b)p(a,b) \]

再次使用乘积规则，这次处理方程右侧的第二项，我们有:

\[p(a,b,c)=p(c|a,b)p(b|a)p(a) \]

这个分解方法对于任意的联合概率分布都成立。我们可以使用一个简单的图模型来表示该式的右侧。

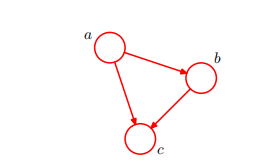
在该图中，我们为每个随机变量\(a,b,c\)都引入一个结点，然后对于每个条件概率分布，都在图中添加一条有向边，边的tail是条件概率中条件对应的随机变量的结点，例如对于因子\(p(c|a,b)\)，会存在从结点\(a,b\)到结点\(c\)的边，而对于因子\(p(a)\),没有输入的边。

对于上图，这个图的概率模型如下:

\[p(x_1,x_2,\cdots,x_7)=p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5) \]

因此形式化一下，贝叶斯网络表示的联合分布是:

\[p(x)=\sum_{k=1}^Kp(x_k|p_{a_k}) \]

其中,\(p_{a_k}\)是\(x_k\)的所有父节点。

条件独立的三种情况

条件独立这个概念，我们在朴素贝叶斯中接触过，意思是给定\(a,b,c\)，如果\(p(a,b|c)=p(a|c)p(b|c)\)，则说明给定\(c\)，\(a\)和\(b\)条件独立。在贝叶斯网络中，条件独立的图模型主要有以下三种情况:

第一种情况tail-to-tail

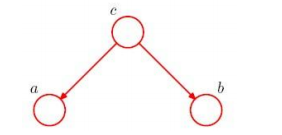
\(C\)位于两个箭头的尾部，称作\(tail-to-tail\)，这种情况，\(c\)未知的时候，\(a,b\)是不独立的。\(c\)已知的时候，\(a,b\)条件独立。
在\(c\)未知的时候，\(p(a,b)\)如下求解：

\[p(a,b)=\sum_c{p(a|c)p(b|c)p(c)} \]

可以看出，无法得出:\(p(a,b)=p(a)p(b)\)，所以\(a,b\)不独立。
如果\(c\)已知，则:

\[p(a,b|c)=\frac{p(a,b,c)}{p(c)}=\frac{p(a|c)}{p(b|c)} \]

所以\(a,b\)条件独立于\(c\)。

第二种情况tail-to-head

如图：

这种情况也是\(c\)未知时，\(a\)和\(b\)不独立，\(c\)已知时，\(a\)和\(b\)条件不独立。\(c\)已知时，\(a\)和\(b\)条件独立于\(c\)，推导如下:

\[p(a,b|c)=\frac{p(a,b,c)}{p(c)}=\frac{(p(a)p(c|a)p(b|c)}{p(c)}=p(a|c)(b|c) \]

第三种情况head-to-head

如图:

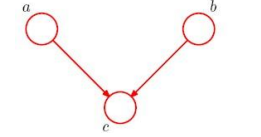
这种情况反过来了，\(c\)未知时，\(a\)和\(b\)是独立的，但当\(c\)已知时，\(a\)和\(b\)不满足条件独立，因为:

\[p(a,b,c)=p(a)p(b)p(c|a,b) \]

计算该概率的边界概率，得：

\[p(a,b)=p(a)p(b) \]

所以\(a\)和\(b\)相互独立。
但是当\(c\)已知时：

\[p(a,b|c)=\frac{p(a,b,c)}{p(c)}=\frac{p(a)p(b)p(c|a,b)}{p(c)} \]

无法得到\(p(a,b|c)=p(a|c)p(b|c)\)

D-seperation

将这三种情况总结，就是贝叶斯网络的一个重要概念，D-separation，这个概念的内容就是:
\(A,B,C\) 三组节点，如果\(A\)中的任意节点与\(B\)的任意节点的所有路径上，存在以下节点，就说\(A\)和\(B\)被\(C\)阻断：

• \(A\)到\(B\)的路径上存在tail-to-tail或head-to-tail形式的节点，并且该节点属于\(C\)
• 路径上存在head-to-head的节点，并且该节点不属于\(C\)
  举个栗子：
  
  在上图中，假设(a)中的\(c\)和（b）中的\(f\)是已知的。
  （a）中，节点\(f\)和节点\(e\)都不是d-seperation的。因为\(f\)是tail-to-tail，但\(f\)不是已知的，因此\(f\)不属于\(C\)。\(e\)是head-to-head，但\(e\)的子节点\(c\)是已知的，所以\(e\)也不属于\(C\)。
  同理（b）中，\(f\)和\(e\)都是d-seperation。

贝叶斯网络模型

• 单一: 朴素贝叶斯
• 混合: GMM
• 时间: 马尔科夫链 、 高斯过程
• 连续: 高斯贝叶斯网络

总结: 因为有了这些条件独立的规则，我们可以将图理解成一个filter。即给定一系列随机变量，其联合分布\(p(x_1,x_2,\cdots,x_n)\)，理论上可以分解成各种条件分布的乘积，但过一遍图，不满足图表示依赖关系和条件独立的分布就被过滤掉。所以图模型，用不同随机变量之间的链接表示各种关系，可以表示复杂的分布模型。