区间贪心算法 结合优先队列使用效果更佳——以POJ 2376、1328、3190为例
贪心算法题目很多本质上都是区间贪心,这次就主要讨论以区间为载体进行的贪心算法。
我们以POJ上的这三道题目为例,分析一下这类型题目的主要思想,难度依次递进啦~
POJ 2376: Cleaning Shifts
题目
Description
Farmer John is assigning some of his N (1 <= N <= 25,000) cows to do some cleaning chores around the barn. He always wants to have one cow working on cleaning things up and has divided the day into T shifts (1 <= T <= 1,000,000), the first being shift 1 and the last being shift T.
Each cow is only available at some interval of times during the day for work on cleaning. Any cow that is selected for cleaning duty will work for the entirety of her interval.
Your job is to help Farmer John assign some cows to shifts so that (i) every shift has at least one cow assigned to it, and (ii) as few cows as possible are involved in cleaning. If it is not possible to assign a cow to each shift, print -1.
Input
-
Line 1: Two space-separated integers: N and T
-
Lines 2..N+1: Each line contains the start and end times of the interval during which a cow can work. A cow starts work at the start time and finishes after the end time.
Output
- Line 1: The minimum number of cows Farmer John needs to hire or -1 if it is not possible to assign a cow to each shift.
Sample Input
3 10
1 7
3 6
6 10
Sample Output
2
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
INPUT DETAILS:
There are 3 cows and 10 shifts. Cow #1 can work shifts 1..7, cow #2 can work shifts 3..6, and cow #3 can work shifts 6..10.
OUTPUT DETAILS:
By selecting cows #1 and #3, all shifts are covered. There is no way to cover all the shifts using fewer than 2 cows.
题解
题目大意
给定N个小区间以及区间起点终点,求能用它们覆盖区间[1,T]的最小组合。
思路
这道题的贪心策略是从左往右,尽量选择长度最大的区间。
那么我们首先对所有奶牛排序,按照开始时间排序。
然后更新起点=终点+1,搜索剩下的奶牛中能够覆盖这个起点同时终点最远的那一头,更新终点。
代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=25010;
struct Intervals
{
int st;
int ed;
};
bool cmp(const Intervals &a,const Intervals &b)
{
return a.st==b.st?a.ed<b.ed:a.st<b.st;
}
int n,t;
Intervals cows[maxn];
int solve()
{
int cnt=0,start=1,cur=0;
for(int i=0;i<n;i++)
{
if(start>t)
return cnt;
if(cows[i].st<=start)
cur=max(cur,cows[i].ed);
else if(cows[i].st>start)
{
cnt++;
start=cur+1;
if(cows[i].st<=start)
cur=max(cur,cows[i].ed);
else
return -1;
}
}
if(start<=t&&cur>=t)
return cnt+1;
if(cur<t)
return -1;
return cnt;
}
int main()
{
scanf("%d %d",&n,&t);
for(int i=0;i<n;i++)
scanf("%d %d",&cows[i].st,&cows[i].ed);
sort(cows,cows+n,cmp);
int res = solve();
printf("%d\n",res);
return 0;
}
小贴士:对于区间类型的题目,我们一定要仔细审题,注意选择的前后区间的两个端点,即前一个区间的右端点和后一个区间的左端点是需要相同还是相差1。比如这道题就是这两个端点不能相同,相同就算覆盖了,[1,3],[4,5]才算是连续的符合条件的区间,[1,3],[3,5]是不合题意的,如果因为审题上的小错误一直WA,那就很惨了。
然后为大家提供一些友情数据:
input:
10 10
1 3
2 4
3 5
4 6
5 7
6 8
7 9
8 10
9 10
10 10
output:
4
input:
2 10
1 4
5 10
output:
2
POJ 1328: Radar Installation
题目
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
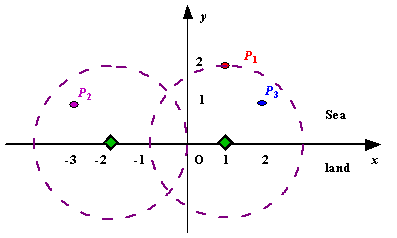
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input:
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
题解
这道题乍一看,好像有点复杂的样子,但是我们稍微转换一下,其实这道题就是披着区间贪心的小绵羊。
题目大意
平面直角坐标系上有n个点,求在x轴上找尽量少的点,以这些点为圆心画一个半径为d的圆,使得给定的点都在画出来的圆里。如果不能输出-1。
思路
如果直接画圆来贪心的满足各个岛屿的话,圆的位置其实是不好确定的,直接先满足最高的点然后平移圆不一定是最优策略,所以不妨反过来想:
以岛屿为圆心画圆,然后记录圆与直线相交的区间,只要雷达放在这个区间内,那么这个岛屿就一定可以被包含
这样问题就变的简单了,用所得的区间按照左端点从小到大排序,从第一个开始,如果和第二个区间有交集,那么这两个岛屿可以共用一个雷达,更新交集,然后同理看第三个区间,直到没有交集,就要增加一个雷达,记录新的区间.
代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=1010;
struct node
{
int x;
int y;
};
struct Interval
{
double a;
double b;
};
bool cmp(const Interval &o1,const Interval &o2)
{
return o1.a<o2.a;
}
node island[maxn];
Interval intervals[maxn];
int n,d;
int solve();
int main()
{
int iCase=0,ansx;
bool flag;
while(scanf("%d %d",&n,&d),n||d)
{
iCase++;
flag=true;
for(int i=0;i<n;i++)
scanf("%d %d",&island[i].x,&island[i].y);
if(d<0)
flag=false;
for(int i=0;i<n;i++)
{
ansx=d*d-island[i].y*island[i].y;
if(ansx<0)
{
flag=false;
break;
}
else
{
intervals[i].a=-sqrt(ansx)+island[i].x;
intervals[i].b=sqrt(ansx)+island[i].x;
}
}
if(flag)
{
sort(intervals,intervals+n,cmp);
int ans = solve();
printf("Case %d: %d\n",iCase,ans);
}
else
printf("Case %d: -1\n",iCase);
}
return 0;
}
int solve()
{
int cnt=1;
double start=intervals[0].a;
double end=intervals[0].b;
for(int i=1;i<n;i++)
{
if(intervals[i].a>=start&&intervals[i].b<=end)
end=min(end,intervals[i].b);
else if(intervals[i].a>end)
{
cnt++;
start=intervals[i].a;
end=intervals[i].b;
}
}
return cnt;
}
算法思想就那么多,但是衍生出来的题目却有千万道,所以我们一定要学会转化。
再为大家提供一些辅助的测试数据:
input:
2 5
-3 4
-6 3
4 5
-5 3
-3 5
2 3
3 3
20 8
-20 7
-18 6
-5 8
-21 8
-15 7
-17 5
-1 5
-2 3
-9 6
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 7
9 6
10 5
0 0
2 3
0 2
2 3
2 3
0 2
1 3
3 3
1 2
-3 2
2 4
8 5
2 4
-4 4
-3 3
-3 1
-3 0
-1 0
0 5
6 0
3 0
1 2
-3 1
2 1
3 2
1 2
-3 1
2 1
1 2
0 2
2 3
0 2
2 3
4 -5
4 3
4 3
2 3
6 -9
3 -3
1 2
-3 2
2 1
6 2
1 2
1 2
1 2
-3 1
2 1
0 0
1 2
0 2
2 3
0 2
1 3
3 10
1 10
2 3
4 5
3 5
1 10
2 3
4 5
4 7
1 10
2 3
4 5
0 0
3 9
1 10
2 3
4 5
0 0
output:
Case 1: 1
Case 2: 2
Case 3: 4
Case 4: 1
Case 5: 1
Case 6: -1
Case 7: 3
Case 8: -1
Case 9: 2
Case 10: 1
Case 11: 1
Case 12: -1
Case 13: -1
Case 14: 2
Case 15: 1
Case 16: 1
Case 17: 1
Case 18: -1
Case 19: -1
Case 20: -1
POJ 3190: Stall Reservations
题目
Description
Oh those picky N (1 <= N <= 50,000) cows! They are so picky that each one will only be milked over some precise time interval A..B (1 <= A <= B <= 1,000,000), which includes both times A and B. Obviously, FJ must create a reservation system to determine which stall each cow can be assigned for her milking time. Of course, no cow will share such a private moment with other cows.
Help FJ by determining:
- The minimum number of stalls required in the barn so that each cow
- can have her private milking period
An assignment of cows to these stalls over time
Many answers are correct for each test dataset; a program will grade your answer.
Input
Line 1: A single integer, N
Lines 2..N+1: Line i+1 describes cow i's milking interval with two space-separated integers.
Output
Line 1: The minimum number of stalls the barn must have.
Lines 2..N+1: Line i+1 describes the stall to which cow i will be assigned for her milking period.
Sample Input
5
1 10
2 4
3 6
5 8
4 7
Sample Output
4
1
2
3
2
4
Hint
Explanation of the sample:
Here's a graphical schedule for this output:
Time 1 2 3 4 5 6 7 8 9 10
Stall 1 c1>>>>>>>>>>>>>>>>>>>>>>>>>>>
Stall 2 .. c2>>>>>> c4>>>>>>>>> .. ..
Stall 3 .. .. c3>>>>>>>>> .. .. .. ..
Stall 4 .. .. .. c5>>>>>>>>> .. .. ..
Other outputs using the same number of stalls are possible.
题解
题目大意
每一只奶牛要求在时间区间[A,B]内独享一个牛栏。问最少需要多少个牛栏。
思路
贪心策略是优先满足A最小的奶牛,维持一个牛栏B最小堆,将新来的奶牛塞进B最小的牛栏里。
所以这道题目我们可以使用优先队列来帮助我们维护这个最小堆。在贪心算法的题目中,优先队列是一个很好的辅助数据结构,大家要多多使用它。
- 奶牛是需要排序的,但是输出的顺序必须是按题目中给出的顺序,因此需要给每只奶牛编号,这个可以在奶牛的结构体中添加一个index的编号.
- 为了使得尽量使得区间不相交,对奶牛排序,一级排序按开始时间递增(最先开始的优先选择),二级排序按结束时间递增
- 使用优先队列,队列中的元素代表当前在产奶的奶牛,队列中的元素结束时间的较小者优先出队,保证尽量空出来多的房子
- 当新加入一只奶牛时,如果队首奶牛还没有产奶结束,只能新使用一个房子,否则就使用当前队首的奶牛使用的房子,并且把队首的奶牛出队(产奶结束)
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=50010;
const int maxb=1000010;
int n;
struct Interval
{
int a;
int b;
int stall;
int index;
bool operator<(const Interval &o2)const
{
return b>o2.b;
}
};
Interval cows[maxn],tempcows[maxn];
bool cmpbya(const Interval &o1,const Interval &o2);
bool cmpbyindex(const Interval &o1,const Interval &o2);
int solve();
int main()
{
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<n;i++)
{
scanf("%d %d",&cows[i].a,&cows[i].b);
cows[i].index=i;
}
sort(cows,cows+n,cmpbya);
int res=solve();
printf("%d\n",res);
sort(cows,cows+n,cmpbyindex);
for(int i=0;i<n;i++)
printf("%d\n",cows[i].stall);
}
return 0;
}
bool cmpbya(const Interval &o1,const Interval &o2)
{
return o1.a==o2.a?o1.b<o2.b:o1.a<o2.a;
}
bool cmpbyindex(const Interval &o1,const Interval &o2)
{
return o1.index<o2.index;
}
int solve()
{
int cnt=1;
priority_queue<Interval> q;
cows[0].stall=1;
q.push(cows[0]);
for(int i=1;i<n;i++)
{
Interval temp = q.top();
if(cows[i].a<=temp.b)
{
cnt++;
cows[i].stall=cnt;
}
else if(cows[i].a>temp.b)
{
cows[i].stall=temp.stall;
q.pop();
}
q.push(cows[i]);
}
return cnt;
}




