python（第三周作业）续上

算24

描述

给出4个小于10的正整数，可以使用加、减、乘、除4种运算以及括号把4个数连接起来得到一个表达式。现在问题是，是否存在一种方式使得所得表达式的结果等于24。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬

这里加、减、乘、除以及括号的运算结果和运算优先级跟平常定义一致。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬

         例如，对于5，5，5，1，可知5×（5－1／5）＝24。又如，对于1，1，4，2无论如何都不能得到24

输入格式

     在代码中的输入部分输入4个小于10的正整数。输入使用input()，不要增加额外的提示信息。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬

输出格式

      对于每一组测试数据，输出一行，如果可以得到24，输出"YES"其算法；否则“NO”。

from itertools import permutations
a = input()
b = input()
c = input()
d = input()
n = a+b+c+d
sum = 1
for i in n:
    sum *= eval(i)
if sum < 24:
    print("NO")
    exit()
notation = ['+', '-', '*', "/"]
st = set()
num = 0
number = set(permutations(n))#将n进行相应的排列组合
for i in notation:
    s = i
    t1 = notation.copy()
    t1.remove(i)#进行一次就去掉一个运算符
    for j in t1:
        s += j
        t2 = t1.copy()
        t2.remove(j)
        for p in t2:
            s += p
            st.add(s)
            s = i+j
        s = i
newst = set()
for i in number:
    for j in st:
        newst.add(i[0]+j[0]+i[1]+j[1]+i[2]+j[2]+i[3])
# print(newst)
all = set()
for i in newst:
    i1 = '('+i[0:3]+')'+i[3:]
    i2 = i[0:2]+'('+i[2:5]+')'+i[5:]
    i3 = i[0:4] + '(' + i[4:] + ')'
    i4 = '(('+i[0:3]+')'+i[3:5]+")"+i[5:]
    i5 = i[0:2]+'(('+i[2:5]+')'+i[5:]+")"
    i6 = '(' + i[0:2] + '(' + i[2:5] + '))' + i[5:]
    i7 = i[0:2]+'('+i[2:4]+'('+i[4:]+"))"
    all.add(i1)
    all.add(i2)
    all.add(i3)
    all.add(i4)
    all.add(i5)
    all.add(i6)
    all.add(i7)
result = []
for i in all:
    try:
        if eval(i) == 24:
          result.append(i)
    except:
        pass
print("YES")
print("("+sorted(result)[0]+")")

计算24点在打扑克的时候会用到呢

网上挺多计算24点的小窍门，根据所给的公式用python转换出来就可以用啦，代码如上👆！

另外一种计算24点的代码，如下👇，是我在简书上看到的，在那基础上修改了一下

from __future__ import division
from itertools import combinations
import re


class Solver:

    # 需要达成的目标结果值
    target = 24

    # 四则运算符号定义，其中，a -- b = b - a，a // b = b / a
    ops = ['+', '-', '*', '/', '--', '//']

    # precise_mode为精准模式，若开启，则减号及除号后开启括号
    def __init__(self, precise_mode=False):
        self.precise_mode = precise_mode

    def solution(self, nums):
        result = []
        groups = self.dimensionality_reduction(self.format(nums))
        for group in groups:
            for op in self.ops:
                exp = self.assemble(group[0], group[1], op)['exp']
                if self.check(exp, self.target) and exp not in result:
                    result.append(exp)
        return [exp + '=' + str(self.target) for exp in result]

    # 对需要处理的数字或表达式组合进行降维，降低到二维
    def dimensionality_reduction(self, nums):
        result = []

        # 如果维数大于2，则选出两个表达式组合成一个，从而降低一个维度，通过递归降低到二维
        if len(nums) > 2:
            for group in self.group(nums, 2):
                for op in self.ops:
                    new_group = [self.assemble(group[0][0], group[0][1], op)] + group[1]
                    result += self.dimensionality_reduction(new_group)
        else:
            result = [nums]
        return result

    # 将两个表达式组合成一个新表达式
    def assemble(self, exp1, exp2, op):

        # 如果运算符为'--'或者'//'，则交换数字顺序重新计算
        if op == '--' or op == '//':
            return self.assemble(exp2, exp1, op[0])

        # 如果是乘法，则根据两个表达式的情况加括号
        if op in r'*/':
            exp1 = self.add_parenthesis(exp1)
            exp2 = self.add_parenthesis(exp2)

        if self.precise_mode:
            if op == '-':
                exp2 = self.add_parenthesis(exp2)
            elif op == '/':
                exp2 = self.add_parenthesis(exp2, True)

        exp = self.convert(exp1['exp'] + op + exp2['exp'], op)
        return {'op': op, 'exp': exp}

    # 根据需要为表达式添加相应的括号
    @staticmethod
    def add_parenthesis(exp, is_necessary=False):

        # 如果上一计算步骤的运算符号为加号或减号，则需加括号
        if (is_necessary and not exp['exp'].isdigit()) or exp['op'] in r'+-':
            result = {
                'exp': '(' + exp['exp'] + ')',
                'op': exp['op']
            }
        else:
            result = exp
        return result

    # 检查表达式是否与结果相等，考虑到中间步骤的除法，因此不采用相等判断，而是采用计算值和目标值的绝对值是否符合某个精度
    @staticmethod
    def check(exp, target, precision=0.0001):
        try:
            return abs(eval(exp) - target) < precision
        except ZeroDivisionError:
            return False

    # 将表达式各项重新排序成为等价标准表达式
    @staticmethod
    def convert(exp, op):
        if op in r'+-':
            pattern = r'([\+\-]((\(.+\)|\d+)[\*\/](\(.+\)|\d+)|\d+))'
            exp = '+' + exp
        else:
            pattern = r'([\*\/](\(.+?\)|\d+))'
            exp = '*' + exp
        result = ''.join(sorted([i[0] for i in re.findall(pattern, exp)]))
        if len(result) != len(exp):
            result = exp
        return result[1:]

    # 将输入的数字格式化为字典，数字的运算符号为空格，注意不是空字符
    @staticmethod
    def format(nums):
        return [{'op': ' ', 'exp': str(num)} for num in nums]

    # 对表达式列表进行分组，返回列表，[[[n1, n2], [n3, n4]], [[n1, n3], [n2, n4]], ...]
    @staticmethod
    def group(exp_list, counter):

        # 生成以下标号为元素的列表
        index_list = [i for i in range(len(exp_list))]

        # 以下标号列表取出不重复的组合
        combination = list(combinations(index_list, counter))

        # 使用下标得到原表达式并组成最终的结果数组
        for group1 in combination:
            group2 = list(set(index_list) - set(group1))
            yield [
                [exp_list[g1] for g1 in group1],
                [exp_list[g2] for g2 in group2]
            ]

auto_input = True
if auto_input:
    customer_input = list()
    customer_input.append(input(''))
    customer_input.append(input(''))
    customer_input.append(input(''))
    customer_input.append(input(''))

task = Solver()
answer = task.solution(customer_input)

if len(answer) == 0:
    print('NO')
else:
    for a in answer:
        print("YES")
        print(a)
        break  #加入break只会出现第一种符合abcd复合运算=24的式子

加了break的效果

 

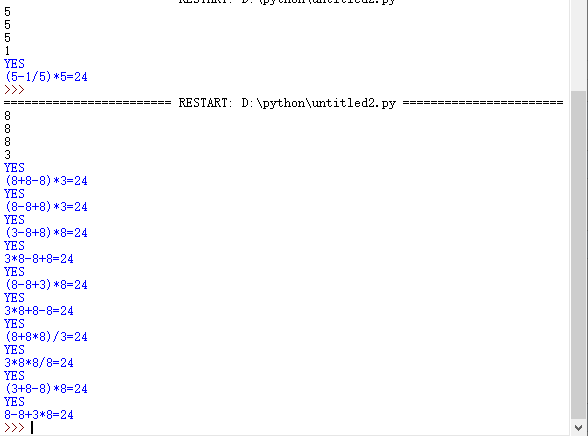不加break的效果

 

愿我们少掉点头发！