【算法】深搜和广搜

深搜和广搜

1.概念

• 深度优先搜索（Depth First Search, DFS）：“不撞南墙不回头”
• 广度优先搜索（Breath First Search, BFS）：“一石激起千层浪”

2.DFS

2.1 特点

• 深度优先搜索的主要思路是从一个未访问过的节点开始，沿着一条路一直走，直到走到头后没法再走了，这时候回退到上一个节点，然后再换下一个节点接着走，不断地去重复这个过程，直到所有的节点都走完，很明显，DFS的特点就是不撞南墙不回头，先走完一条路，再换下一条路接着走。
• 通过上面的叙述，发现DFS其实很多时候是和递归一起出现的，但凡是递归的，当然也可以用非递归的方法来实现，其实就是利用栈这个结构，
• DFS常用于寻找所有解的问题，需要记录并且完成整个搜索，所以很多时候需要去进行剪枝

2.1 典例-树

先来看一下树的DFS，例如要遍历上面那棵树，DFS就是一条路走到黑，然后走不动往上个路口回，然后看有没有其他选择

递归实现

public class Solution {
    private static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int value, Node left, Node right) {
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    public static void dfs(Node treeNode) {
        if (treeNode == null) {
            return;
        }
        // 遍历节点
        process(treeNode)
        // 遍历左节点
        dfs(treeNode.left);
        // 遍历右节点
        dfs(treeNode.right);
    }
}

非递归实现

压入根节点
1.弹出就打印
2.if有右孩子，压入右孩子
3.if有左孩子，压入左孩子
重复1.2.3

/**
 * 使用栈来实现 dfs
 * @param root
 */
public static void dfsWithStack(Node root) {
    if (root == null) {
        return;
    }

    Stack<Node> stack = new Stack<>();
    // 先把根节点压栈
    stack.push(root);
    while (!stack.isEmpty()) {
        Node treeNode = stack.pop();
        // 遍历节点
        process(treeNode)

        // 先压右节点
        if (treeNode.right != null) {
            stack.push(treeNode.right);
        }

        // 再压左节点
        if (treeNode.left != null) {
            stack.push(treeNode.left);
        }
    }
}

2.3 典例-图

思路

假设上幅图片要从起点（黑色）走到终点（红色），找一条路径。
if要用深度优先搜索的例子来解这道题，那对于每一个格子，都有上下左右四个方向，从这个起始的位置可以发现，我们可以按照左->下->右->上这样的顺序去走路，也就是if左边能走，那就往左边走，到了下一个格子后，if左边能走，那接着走，if左边不能走了，那就看看下边能不能走，依次进行，if四个方向都不能走了，那就需要回溯到上一个，然后再看上一个的其他方向能不能走；
具体到这个图中：先向左走1格-》再向左走一格-》左边无法走，下边无法走，上边无法走，右边走过了，无路可走-》这条路死路解决不了问题-》回到上一个位置-》同样无路可走再回退-》到起点后，左边证明不行了，往下走-》。。。。重复这个过程

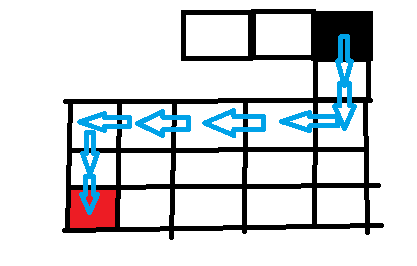
• 深度优先的特点就是不管有多少岔路口，都先选一条路走到底，不成功就返回上一个路口选择下一条路，

程序实现

int goal_x = 9, goal_y = 9   //目标坐标
int n = 10, m = 10   //地图的长宽
int graph[n][m]    
int used[n][m]
int px = {-1, 0, 1, 0}
int py = {0, -1. 0, 1}   //通过这两个来进行左下右中的移动
int flag = 0   //到达终点的标志

void DFS(in graph[][], int used[][], int x, int y)
{
    //if目标相同，那证明成功
    if(graph[x][y] == graph[goal_x][goal_y]){
        print("successful")
        flag = 1
        return
    }
    //向四个方向遍历
    for(int i = 0, i < 4, i++){
        int new_x = x+px[i], new_y = y + py[i]
        if(new_x >= 0 && new_x < n && new_y >= 0 && new_y < m && used[new_x][new_y] == 0 && !flag) {  //没有且满足边界的时候
            used[new_x][new_y] = 1  //走这个格子
            DFS(graph, used, new_x, new_y)   //接着以这个格子接着走
            used[new_x][new_y] = 0  //回溯设置为0
        }
    }
}           

3.BFS

3.1 特点

• 广度优先搜索的主要思路是从一个或多个未访问过的节点开始，先遍历这个节点的所有相邻节点，再遍历每个相邻节点的相邻节点。BFS的特点是一石激起千层浪，从一个节点开始向外扩散。
• DFS是和递归或者说是栈一起出现的，而BFS很多时候其实是和队列一起出现的。这就是两者的区别。
• BFS常用于寻找单一的最短路径问题，特点是：搜到就是最优解

3.2 典例-树

仍然是上面第一个例子，我们换一种遍历思路，刚才是从一条路先走到头，这次一层一层的遍历，这就是bfs

程序实现

/**
 * 使用队列实现 bfs
 * @param root
 */
private static void bfs(Node root) {
    if (root == null) {
        return;
    }
    Queue<Node> stack = new LinkedList<>();
    stack.add(root);

    while (!stack.isEmpty()) {
        Node node = stack.poll();
        System.out.println("value = " + node.value);
        Node left = node.left;
        if (left != null) {
            stack.add(left);
        }
        Node right = node.right;
        if (right != null) {
            stack.add(right);
        }
    }
}

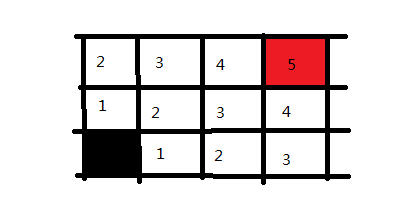
3.3 典例-图

思路

• 广度优先在面临岔路口的时候，会把所有路口都记住，然后向着外面去进行扩散。

程序实现

int n = 10, m = 10;
void BFS(){
    queue que    //用队列来进行保存
    int graph[n][m]
    int px[] = {-1, 0, 1, 0}
    int py[] = {0, -1, 0, 1}
    que.push(起点入队）；
    while(!que.isEmpty()){
        temp = que.pop();
        for(int i = 0; i < 4; i++){
            if(可以走）{
                //标记当前格子
                //入队
            }

4.总结

• 在树里，用的比较多的是dfs，因为树只有两个节点，并且有明显的路径（向左或者向右），可以直接使用递归的方法一次性走完；但是在图里，用到较多的是bfs，对于树而言，队列里存的是当前层的节点；对于图而言，当前队列里存的是所有的邻居节点。

BFS的框架

//计算起点start到终点target的最小距离
int BDS(Node start, Node target){ 
    Queue<Node> queue;  //核心结构：队列；
    Set<Node> visited;  //在图中都会用到，因为存在着交叉，会走回头路，树中则不需要，因为有next指针；
    queue.offer(start);  //起点入队；
    visited.add(start);  
    int step = 0; //记录扩散步数；
    while(queue.isEmpty()){
        int size = queue.size();
        //从当前队列中所有节点向与其关联的节点扩散；
        for(int i = 0; i < size; i++){
            Node cur = queue.poll();
            if(cur == target){
                return step;  //注意不同题目里这里的判断条件，是否到达终点；
            }
            for(Node x : cur.adj()){  //这里指的是当前节点的邻居节点；
                if(!visited.contains(x)){ //还没走过再加入；不走回头路；
                    queue.offer(x);
                    visited.add(x);
                }
            }
        }
        step++;  //注意在这里更新步数；
    }
}

__EOF__

本文作者：Curryxin
本文链接：https://www.cnblogs.com/Curryxin/p/16111576.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！