【算法】排序

目录

• 排序
  • 1.问题引出
  • 2.冒泡排序
    • 2.1 思路
    • 2.2 实现
  • 3.简单选择排序
  • 4. 插入排序
  • 5. 归并排序
  • 6. 快速排序
    • 6.1 思路
    • 6.2 实现
  • 6.3 快速排序和归并排序的区别
  • 7.堆排序
    • 7.1 前提
    • 7.2 思路
    • 7.3 实现
  • 8.总结
  • 参考

排序

1.问题引出

给定一个整数数组，按从小到大的数组将其进行排序；

2.冒泡排序

2.1 思路

冒泡排序应该是最简单的一种排序算法了，其特定是是一种稳定的排序算法；

一般情况下，称某个排序算法稳定，指的是当待排序序列中有相同的元素时，它们的相对位置在排序前后不会发生改变。

假设待排序序列为 (5,1,4,2,8)，如果采用冒泡排序对其进行升序（由小到大）排序，则整个排序过程如下所示：

1. 第一轮排序，此时整个序列中的元素都位于待排序序列，依次扫描每对相邻的元素，并对顺序不正确的元素对交换位置，整个过程下图 所示。
   

2. 第二轮排序，此时待排序序列只包含前 4 个元素，依次扫描每对相邻元素，对顺序不正确的元素对交换位置，整个过程如下图所示。
   

后面的过程同理。

2.2 实现

//冒泡的关键在于for循环的截至条件；
public class BubbleSort{
    public void bubbleSort(int[] arr){
        int l = arr.length;
        for(int i = 0; i < l; i++){  //比较的轮数
            for(int j = 0; j < l-i-1; j++){   //每一轮比较几次；后面排好的几个就不用比了；
                if(arr[j] > arr[j+1]){    //交换前后元素；
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }
}

其实可以稍微优化，也就是剪枝，当中间某一次的时候，if一次交换都没有发生，那就证明已经有序了，就可以结束了，不用再比较了，所以设置一个flag标志位，只有这次交换过元素，下次再执行；

public static void gaijin(int[] arr){
    boolean flag = true;
    for(int i = 0; i < arr.length && flag; i++){
        flag = false;
        for (int j = 0; j < arr.length-1-i; j++){
            if(arr[j] > arr[j+1]){
                swap(arr, j, j+1);
                flag = true;   //只要交换过一次那下次就得接着执行；
                //一旦一次都没交换过，那就证明有序了；不用再执行了；
            }
        }
    }
}
private static void swap(int[] arr, int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

最好情况下就是排好的，遍历一次就行了；

算法	最好时间复杂度	最坏	平均	空间	稳定
冒泡	O(n)	O(n^2)	O(n^2)	O(1)	稳定

3.简单选择排序

冒泡排序是每次都从最开头开始，开始扫描，每经过一轮扫描后最大的元素就能往后挪；中间是通过不断交换完成的；
简单选择排序思想也很简单，分成排好的序和未排好的序列，从未排序的第一个开始，扫描整个未排序数组，找到里面最小的，然后和这个交换，1个元素归位，然后循环；

public class SelectSort {
    public static void  selectSort(int[] arr){
        int min;
        for(int i = 0; i < arr.length; i++){
            min = i;  //初始化未排序数组的第一个为最小，在这里存储的是最小值的索引；
            for(int j = i+1; j < arr.length; j++){
                if(arr[min] > arr[j]) min = j;
            }
            if(min != i) swap(arr, i, min);
        }
    }
    private static void swap(int[] arr, int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

这个选择排序不是稳定的，因为每次都是从未排序的里面找到最小的和这个元素交换，这个元素如果和后面的有个值一样，那一交换可能就到相同的后面了；

算法	最好时间复杂度	最坏	平均	空间	稳定
冒泡	O(n^2)	O(n^2)	O(n^2)	O(1)	不稳定

4. 插入排序

插入排序就和打扑克时理牌的时候一样，把新元素插入到已经排好序的有序表中；

public class InsertSort {
    public static void insertSort(int arr[]){
        //从第2个元素开始
        for(int i = 1; i < arr.length; i++){
            int temp = arr[i];  //要排序的值；
            int j;  //for循环外要用，定义到这；
            for(j = i-1; j >= 0; j--){
                if(temp < arr[j]){
                    arr[j+1] = arr[j]; //小于的话那就等往后移动了；给要插入的腾出空；
                    continue;
                }
                break;   //到这的就说明找到位置了，
            }
            arr[j+1] = temp;  //在这个位置插入；
        }
    }
}

最好情况下就是不用交换，所以时间复杂度O(n)；
一直在移动的是比待插入元素大的值，相对位置没有改变，所以是稳定的；

算法	最好时间复杂度	最坏	平均	空间	稳定
冒泡	O(n)	O(n^2)	O(n^2)	O(1)	稳定

5. 归并排序

归并排序是利用分治的思想进行的，分：将问题分成一个个小问题然后递归求解，治：将各阶段子问题的答案拼在一起，分而治之；

治的过程其实就是合并两个有序子序列；这也是一道经典的例题；新建一个新数组

public class MergeSort {
    public void mergeSort(int[] arr, int left, int right){
        if(left < right){
            int mid = left + ((right-left) >> 1);
            mergeSort(arr, left, mid); //左归并，使得左有序；
            mergeSort(arr, mid+1, right); //右归并，使得右有序；
            merge(arr, left, mid, right);  //合并两个有序序列过程；
        }
    }
    public void merge(int[] arr, int left, int mid, int right){
        //1.定义临时数组；
        int[] temp = new int[right-left+1];
        int i = left;   //左序列指针；
        int j = mid+1;  //右序列指针；
        int index = 0; //临时数组指针；
        while(i <= mid && j <= right){
            if(arr[i] <= arr[j]){
                temp[index++] = arr[i++];
            }else{
                temp[index++] = arr[j++];
            }
        }
        while(i <= mid){   //将左边剩余填充temp；
            temp[index++] = arr[i++];
        }
        while(j <= right){
            temp[index++] = arr[j++];
        }
        index = 0;
        //将temp中的元素拷贝到原数组中；
        while (left <= right){
            arr[left++] = temp[index++];
        }
    }
}

归并排序一层一层的折半分组，整个排序过程需要logn，所以整体复杂度是O(nlogn)；

算法	最好时间复杂度	最坏	平均	空间	稳定
冒泡	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定

6. 快速排序

6.1 思路

分而治之
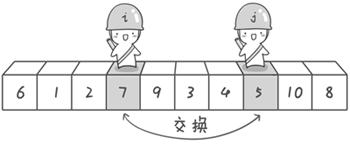
比如说我们要排序：“6 1 2 7 9 3 4 5 10 8”；
1.从序列两端开始探测，先从右往左找一个小于6的数，再从左往右找一个大于6的数，然后交换他们。

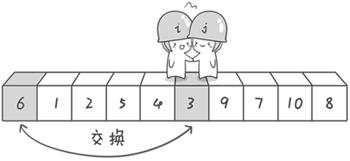
2.接着上述步骤，直到两个人遇上了，说明此次探测结束；将遇上的元素和6交换；

注意 这时候相遇的一定是比6小的，原因：因为每次都是先从右往左走，也就是每次都是哨兵j先动，j先停，所以只要它停下来一定是比6小的，所以最后可以放心交换6与相遇的位置；
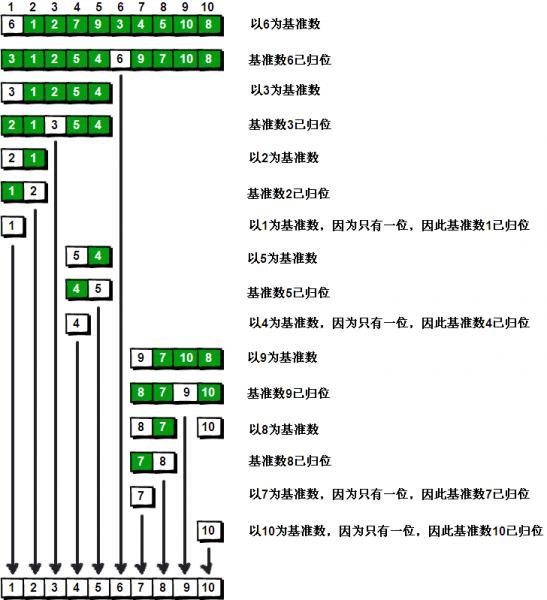
经过第一轮探测后原序列以6为分界点，左边都比6小，右边都比6大；这个6已经到了自己正确的位置上，归位完毕；
3.分别按照上述思路处理左右两个序列；

快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N2)，它的平均时间复杂度为O(NlogN)。

6.2 实现

public class QuickSort{
    public void quickSort(int[] arr, int head; int tail){
        if(tail < head) return;  //设置递归终止条件；也就是只有两个元素的时候，j和i相遇就是在i处，传进j-1就变成了小于head的；
        int i = head, j = tail;
        int temp = arr[head];  //基准位；
        while(i < j){
        //一定要从右边开始，目的其实是为了让停下来的元素是小于基准元素的，
        //然后再互换的时候，保证换完之后基准左边的都是小于基准的；
            while(i < j && arr[j] >= temp){ 
                j--;
            }
            while(i < j && arr[i] <= temp){
                i++;
            }
            if(i < j){
                int t = arr[i];
                arr[i] = arr[j];
                arr[j] = t;
            }
        }
        //到这里一轮结束，交换相遇的和基准位的；
        arr[head] = arr[j];   
        arr[j] = temp; //基准位归位；
        quickSort(arr, head, j-1);  //快排左边序列；
        quickSort(arr,j+1,tail);  //快排右边序列；
    }
}

快速排序的复杂度取决于递归树的深度，if每次两个分区都差不多大，那是O(nlogn)，但是也可能划分很不均匀，近似线性，那时间复杂度就是O(n^2);此外快速排序这种比较和交换是跳跃式的，所以是不稳定的；

算法	最好时间复杂度	最坏	平均	空间	稳定
冒泡	O(nlogn)	O(n^2)	O(nlogn)	O(1)	不稳定

6.3 快速排序和归并排序的区别

• 快速排序和归并排序都是采用了分治的思想，快速排序是自上而下，分区以后再去处理子问题，此外，快速排序是原地进行的，不用开辟新空间；
• 归并排序是是自下而上的，先处理子问题以后再合并，而且归并排序是非原地的，需要有内存空间开辟；

7.堆排序

7.1 前提

如果要弄懂堆排序，首先最起码要知道堆吧，堆是一颗顺序存储的完全二叉树，堆有两种分类：

• 大根堆：每个子树的根节点都不小于孩子节点；
• 小根堆：每个子树的根节点都不大于孩子节点；
  Ri >= R2i+1且Ri >= R2i+2(大根堆)；
  Ri <= R2i+1且Ri <= R2i+2(大根堆)；

因为是完全二叉树，所以完全可以用数组去存，原因就是可以根据索引能够得到节点
比如这就是明显的一个小根堆：

7.2 思路

1.根据初始数组去构造初始堆(构建一个完全二叉树，所以父节点都比孩子节点大，从最后一个树依次向上，直到最上面)；

2.每次交换第一个和最后一个元素，输出最后一个元素(最大值)，然后把剩下元素重新调整为大根堆；

7.3 实现

public class HeapSort {
    public void headSort(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }
        int len = arr.length;
        buildMaxHaep(arr, len);  //构建大根堆，其实就是将待排序数组变成大根堆结构数组；
        for(int i = len-1; i > 0; i--){
            swap(arr, 0,i);  //交换堆顶和当前末尾的，重置大根堆；
            len--;
            adjustHeap(arr, 0, len);
        }
    }
    private void buildMaxHaep(int[] arr, int len){
        for(int i = len/2-1; i >= 0; i--){  //最后一个非叶子节点索引；
            adjustHeap(arr, i, len);
        }
    }
    private void adjustHeap(int[] arr, int i, int len){  //i是根节点，len是长度
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int max = i;
        if(left < len && arr[left] > arr[max]){   //找根、左、右3个的最大；
            max = left;
        }
        if(right < len && arr[right] > arr[max]){
            max = right;
        }
        if(max != i){
            swap(arr, i, max);
            adjustHeap(arr, max, len);  //互换之后，子节点的值变了，需要再次调整；
        }
    }
    private void swap(int[] arr, int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

建堆的时间复杂度是O(n)，总的时间复杂度是O(nlogn)；
堆排序也是跳跃式的交换，所以不是稳定的；

8.总结

参考

参考链接1：冒泡排序
参考链接1：快速排序
排序总结

__EOF__

本文作者：Curryxin
本文链接：https://www.cnblogs.com/Curryxin/p/15014639.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！