【算法】KMP算法

KMP算法

1.问题引出

字符串匹配问题

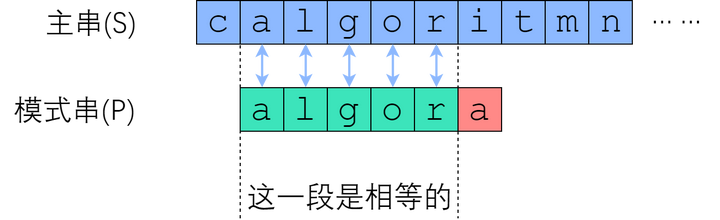
所谓字符串匹配，是这样一种问题：“字符串 P 是否为字符串 S 的子串？如果是，它出现在 S 的哪些位置？” 其中 S 称为主串；P 称为模式串。也就是在S串中找P串，并返回S串中出现的位置；
也就是leetcode的第28题

2. Brute-Force（暴力解法）

2.1 思路

这个解法比较简单，就是让主串和模式串从头开始，一个一个比较，如果一致就比较下一个字符，不一致时就把模式串往后移动一位（在实际中不可能让模式串移动，其实就是让模式串的首位对上主串的下一个，与模式串移动是等效的的）。

2.2 代码实现：

public int BF(String s, String p){
    int m = s.length();
    int n = p.length();
    for(int i = 0; i <= s-n; i++){  //控制主串比较的位置；
        boolean flag = true;
        for(int j = 0; j < n; j++){   //控制模式串比较的位置；每次都从头比较；
            if(s.charAt(i+j) != p.charAt(j)){
                break;
                flag = false;
            }
        }
        if(flag){
            return i;
        }
    }
    return -1;
}

很明显这种做法的时间复杂度是O(M*N)

3. KMP算法

3.1 KMP匹配

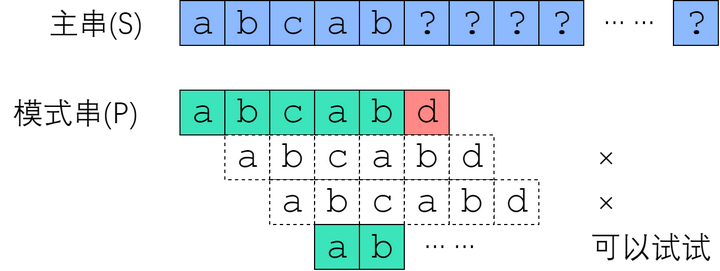
在BF解法中，如果比较不成功，直接就从下一个开始比较，没有从上次中得到有用信息，没有学到东西，那上次失败有什么信息可以利用呢？如果 S[i : i+len(P)] 与 P 的匹配是在第 r 个位置失败的，那么从 S[i] 开始的 (r-1) 个连续字符，一定与 P 的前 (r-1) 个字符一模一样!

跳过不可能的

可以看上图，如果在abcab重合了，在第6个位置不匹配了，那之前的5个是一模一样的，如果像BF中一步一步往后移，那就没有跳过那些不可能的，观察到，从 S[1] 开始肯定没办法成功，因为 S[1] = P[1] = 'b'，和 P[0] 并不相等。从 S[2] 开始也是没戏的，因为 S[2] = P[2] = 'c'，并不等于P[0]. 但是从 S[3] 开始是有可能成功的——至少按照已知的信息，我们推不出矛盾，可以来试试。

KMP 为什么相比于朴素解法更快：

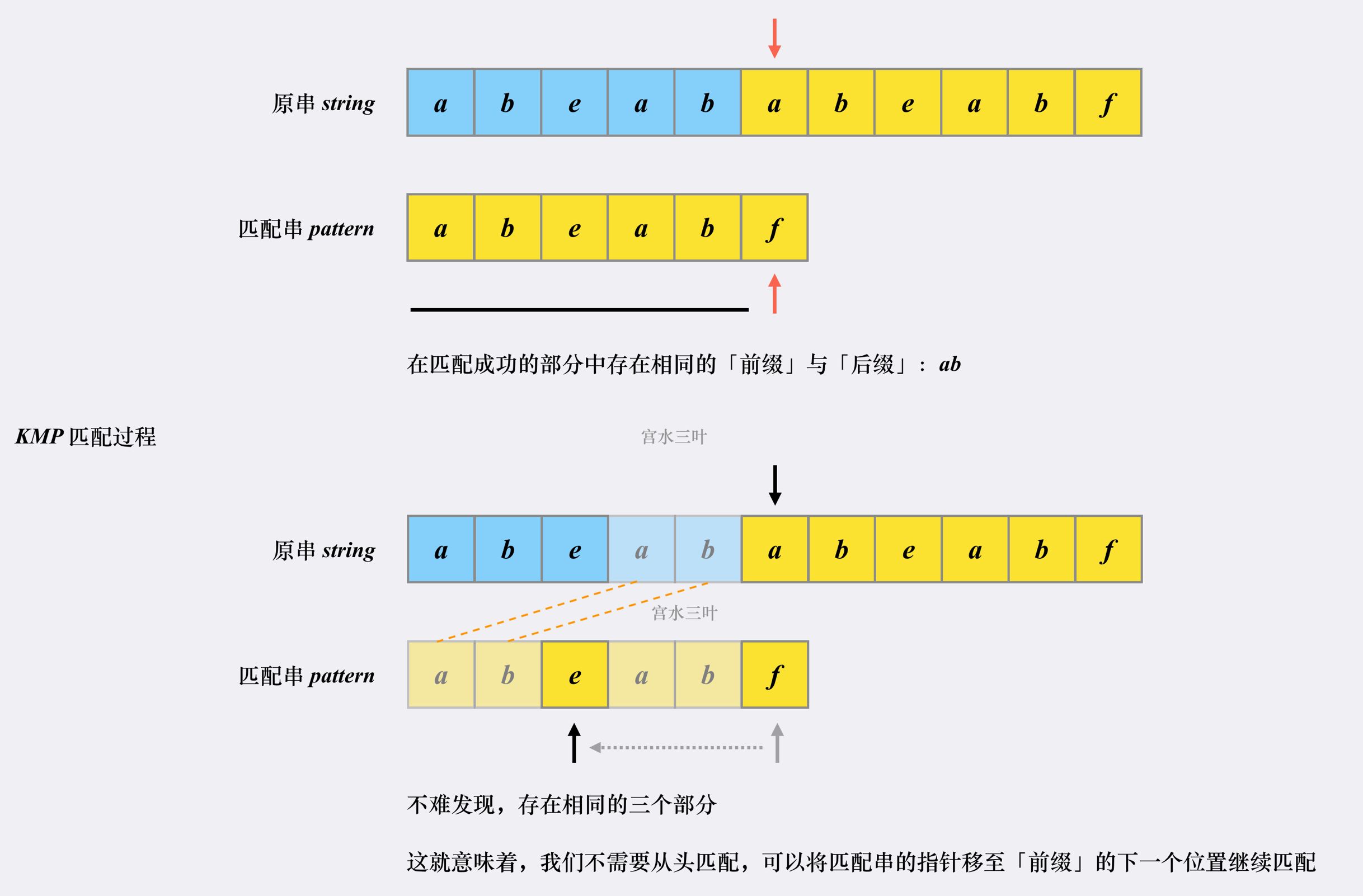
• 因为 KMP 利用已匹配部分中相同的「前缀」和「后缀」来加速下一次的匹配。
• 因为 KMP 的主串指针不会进行回溯（没有朴素匹配中回到下一个「发起点」的过程）。主串指针始终是在右移；其实是意味着：随着匹配过程的进行，原串指针的不断右移，我们本质上是在不断地在否决一些「不可能」的方案。

3.2 next数组

定义：next[i] 表示 P[0] ~ P[i] 这一个子串，使得 前k个字符恰等于后k个字符 的最大的k. 也叫做最大前后缀；通俗的说，其实就是从最后往前看，我们想用最前面的几个元素匹配上最后面的几个元素，让这个值最大。因为这样我们就可以像上面说的跳过那些没用的，然后去从匹配上的去试；
个人理解： 最多能用前面几个去顶替我们末尾几个!

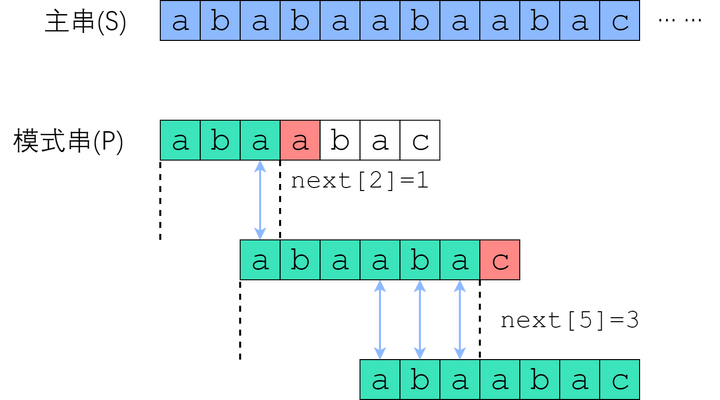
在 S[0] 尝试匹配，失配于 S[3] <=> P[3] 之后，我们直接把模式串往右移了两位，（其实就是让在p[3]处的指针回溯到了next[3-1]=1处，让模式串0处的a替换了模式串2中的a，去匹配上了主串中2中a，接着比较两个串中指针所指向的值）让 S[3] 对准 P[1]. 接着继续匹配，失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位，把 S[8] 对准 P[3]. 此后继续匹配直到成功。
比如next[5]=3含义：如果第5个是最后一个，那么最多有最前面3个能匹配上从最后往前数三个，所以就可以用最前面3个代替最后3个，直接从第4个开始比较：如果next[5]=1含义：如果第5个最后一个元素，那么最多有最前面1个能匹配上最后面往前数一个，所以就可以把中间那些都跳过去了，因为不可能匹配上；
所以next数组为我们移动模式串提供了依据，并且next数组是只取决于模式串；
可能会有一个疑问：比如说ababca，我到了最后一个a处匹配不上了，那按照上面的解法，现在应该看a处前一位也就是c的对应next值，很明显next[4]是0，所以模式串的指针就移动到最开始，也就等于将模式串的首位直接对齐到了主串中原本与a不匹配的那个位置，中间可能错过某些可能吗？比如说我最开始的ab可以移动到2,3位置处，那也是ab说不定可能呢，其实这是不可能的，为什么呢，反证法；如果0和1处的ab匹配上了2和3处的ab，那么后一个一定不匹配，因为如果匹配的话，那就是说前3个能匹配上后3个，那next[4]就等于3而不是0了，所以这也就说明了为什么我们是看前一个也就是看c的next值，因为无论怎样，我们都是要经过它的，如果不看它，那它前面几个匹配上了，到它也匹配不上；
现在问题就变成了如何构建next数组
核心就在于我们要利用已经知道的next[i-1]来求得next[i];
双指针：定义两个指针，一个在前一个在后，一个是从左到右依次直到最后，是用来比较的，一个是每次都是在我们前k个的k处；

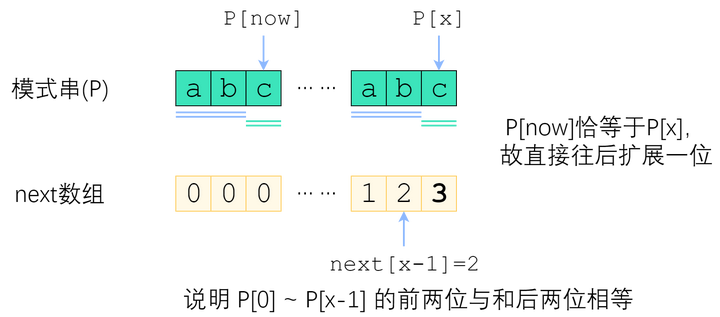
• P[x] = P[now]

• P[x] != P[now]
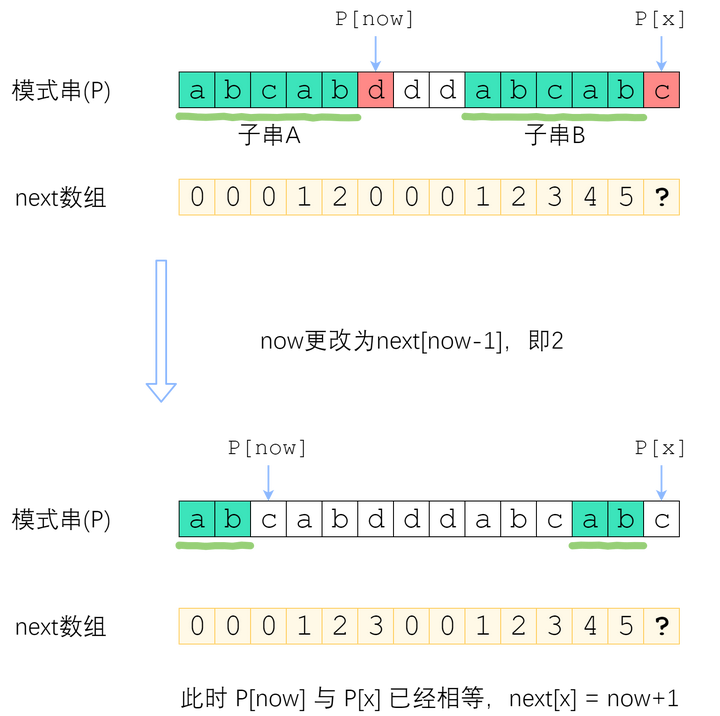
  如图。长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀。可惜 A 右边的字符和 B 右边的那个字符不相等，next[x]不能改成 now+1 了。因此，我们应该缩短这个now，把它改成小一点的值，再来试试 P[x] 是否等于 P[now].
  now该缩小到多少呢？显然，我们不想让now缩小太多。因此我们决定，在保持“P[0]~P[x-1]的now-前缀仍然等于now-后缀”的前提下，让这个新的now尽可能大一点。 P[0]~P[x-1] 的公共前后缀，前缀一定落在串A里面、后缀一定落在串B里面。换句话讲：接下来now应该改成：使得 A的k-前缀等于B的k-后缀 的最大的k.
  可以利用的一个关键信息：串A和串B是相同的！所以B的后缀就等于A的后缀；因此，使得A的k-前缀等于B的k-后缀的最大的k，其实就是串A的最长公共前后缀的长度 —— next[now-1]！

3.3 代码实现

public int KMP(String s, String p){
    int tar = 0;
    int pos = 0;
    char[] arrs = s.toCharArray();
    char[] arrp = p.toCharArray();
    int m = s.length();
    int n = p.length();
    int[] next = buildNext(arrp, n);
    while(tar < m){
        if(arrs[tar] == arrp[pos]){
            tar++;    //匹配则比较下一个元素；
            pos++;     
        }else if(pos != 0){
            pos = next[pos-1];   //不匹配且没回到头，回溯；
        }else{
            tar++;   //回到头证明此tar匹配不上了，右移；
        }
        if(pos == n){   //走完模式串后即匹配成功了；
            return tar-pos;
        }
    }
    return -1;
}

//构建next数组；
private int[] buildNext(char[] p, int n){
    int[] next = new int[n];
    int now = 0;
    int i = 1;
    while(i < n){
        if(p[now] == p[i]){
            now++;    //一致时填充next并移动指针；
            next[i] = now;
            i++;
        }else if(now != 0){   //缩小now；
            now = next[now-1];
        }else{
            next[i] == 0;   //now回到头了，还不一致，直接给next对应位置填0，接着右移；
            i++;
        }
    }
    return next;
}

KMP匹配时tar指针和构建next数组时i指针都是始终右移，没有回溯；
时间复杂度：O(M+N);

参考

参考链接1
参考链接2
参考链接3

__EOF__

本文作者：Curryxin
本文链接：https://www.cnblogs.com/Curryxin/p/15014196.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！