poj1655 Balancing Act求树的重心

Description

Consider a tree T with N (1 <= N <= 20,000) nodes numbered 1...N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T. 
For example, consider the tree: 

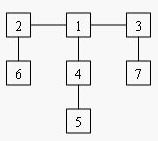
Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two. 

For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number. 

Input

The first line of input contains a single integer t (1 <= t <= 20), the number of test cases. The first line of each test case contains an integer N (1 <= N <= 20,000), the number of congruence. The next N-1 lines each contains two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.

Output

For each test case, print a line containing two integers, the number of the node with minimum balance and the balance of that node.

Sample Input

1
7
2 6
1 2
1 4
4 5
3 7
3 1

Sample Output

1 2



这是一个模板题，是点分治的基础。我们先随便把一个结点作为根，求出siz数组，siz[i]表示以i为根的子树的大小（dfs/bfs都可以，我就用bfs了），然后去掉结点i后的最大块的大小就是max(n-siz[i],i的所有儿子中的最大siz)，这样就做好了。

program rrr(input,output);
type
  etype=record
     t,next:longint;
  end;
var
  e:array[0..40040]of etype;
  a,q,father,siz,f:array[0..20020]of longint;
  v:array[0..20020]of boolean;
  tt,i,j,n,x,y,cnt,h,t,ans,min:longint;
function max(a,b:longint):longint;
begin
   if a>b then exit(a) else exit(b);
end;
procedure add(x,y:longint);
begin
   inc(cnt);e[cnt].t:=y;e[cnt].next:=a[x];a[x]:=cnt;
end;
begin
   assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output);
   readln(tt);
   for i:=1 to tt do
      begin
         readln(n);
         for j:=1 to n do a[j]:=0;cnt:=0;
         for j:=1 to n-1 do begin read(x,y);add(x,y);add(y,x); end;
         fillchar(v,sizeof(v),false);
         h:=0;t:=1;q[1]:=1;v[1]:=true;
         while h<t do
            begin
               inc(h);
               j:=a[q[h]];
               while j<>0 do
                  begin
                     if not v[e[j].t] then
                        begin
                           v[e[j].t]:=true;father[e[j].t]:=q[h];
                           inc(t);q[t]:=e[j].t;
                        end;
                     j:=e[j].next;
                  end;
            end;
         for j:=1 to n do siz[j]:=1;
         fillchar(f,sizeof(f),0);min:=n;
         for j:=n downto 2 do
            begin
               t:=max(f[q[j]],n-siz[q[j]]);
               if (t<min) or (t=min) and (q[j]<ans) then begin ans:=q[j];min:=t; end;
               inc(siz[father[q[j]]],siz[q[j]]);
               if siz[q[j]]>f[father[q[j]]] then f[father[q[j]]]:=siz[q[j]];
            end;
         if f[1]<=min then begin ans:=1;min:=f[1]; end;
         writeln(ans,' ',min);
      end;
   close(input);close(output);
end.