8.线段树
《玩转数据结构》-liuyubobobo 课程笔记
不是重点,一般竞赛才考察,面试一般不考察,只做了解即可
线段树(区间树)
每一个节点存储一个线段或一个区间响应的信息
大多数情况下,区间本身是固定的
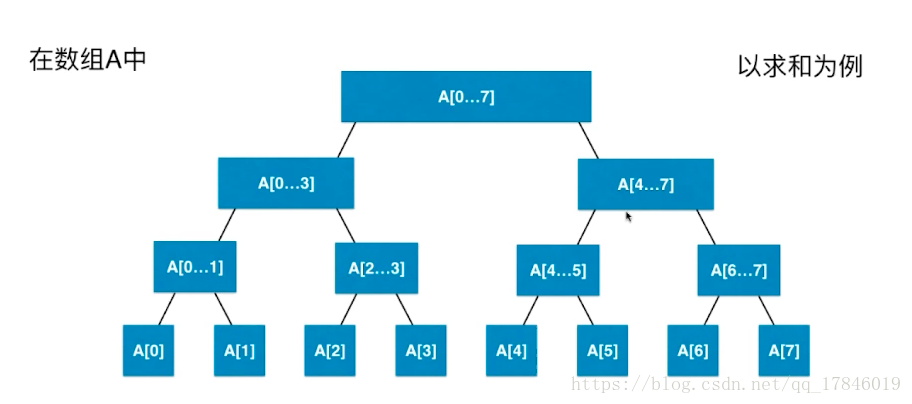
为什么要使用区间树?
对于给定区间
- 更新:更新区间中一个元素或者一个区间的值O(logn) ;数组的实现是O(n)级别
- 查询:查询一个区间[i,j]的最大值,最小值,或者区间数字和O(logn);数组的实现是O(n)级别
优势:在查询某个关心的区间的时候,不用将区间中每个元素都遍历一遍。比如我想查询区间4-7,那么直接访问A[4...7]节点就行了,不用再去访问其中的每一个元素。又比如我想查询区间2-5,那么我则需要访问A[2..3]和A[4..5]两个节点,然后对这两个节点进行合成,组成想要的结果。所以,当数据量非常大的时候,我们仍然可以非常快的找到,我们关心得那个区间,对应的在一个或者多个节点,对其节点的内容进行操作,而不用对这个区间中的每一个元素进行一次遍历。
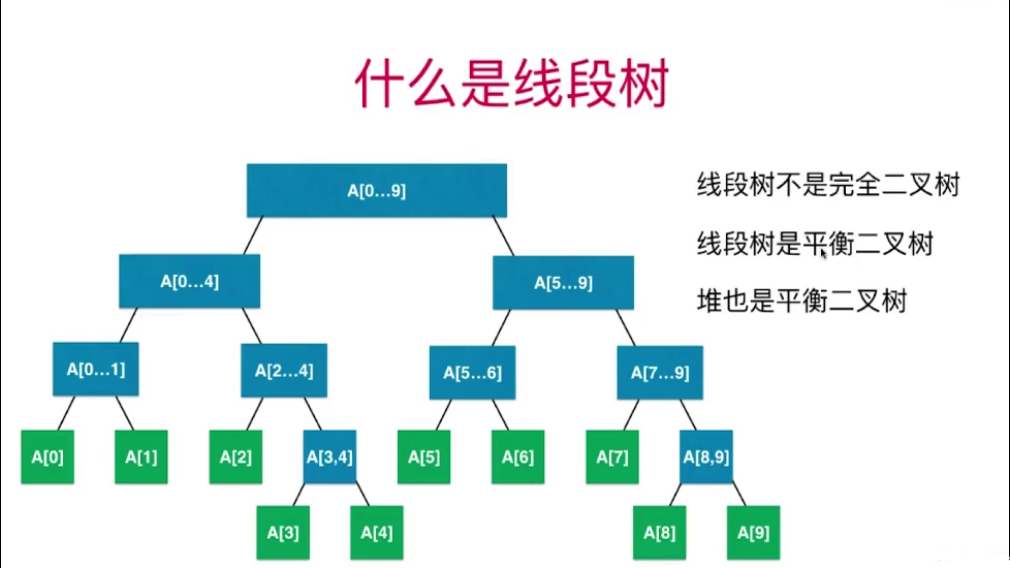
线段树基础表示
-
线段树不是一定完全二叉树或满二叉树
-
线段树是一个平衡二叉树(对于整颗二叉树的叶子节点的最大的深度和它最小的深度差最大不超过1 ,其优势在于不会退化成链表,其树的高度与节点的关系一定是log的关系,使得在平衡二叉树上进行搜索和查询是非常高效的)
-
堆也是一个平衡二叉树(完全二叉树一定是平衡二叉树)
-
二分搜索树不是平衡二叉树
-
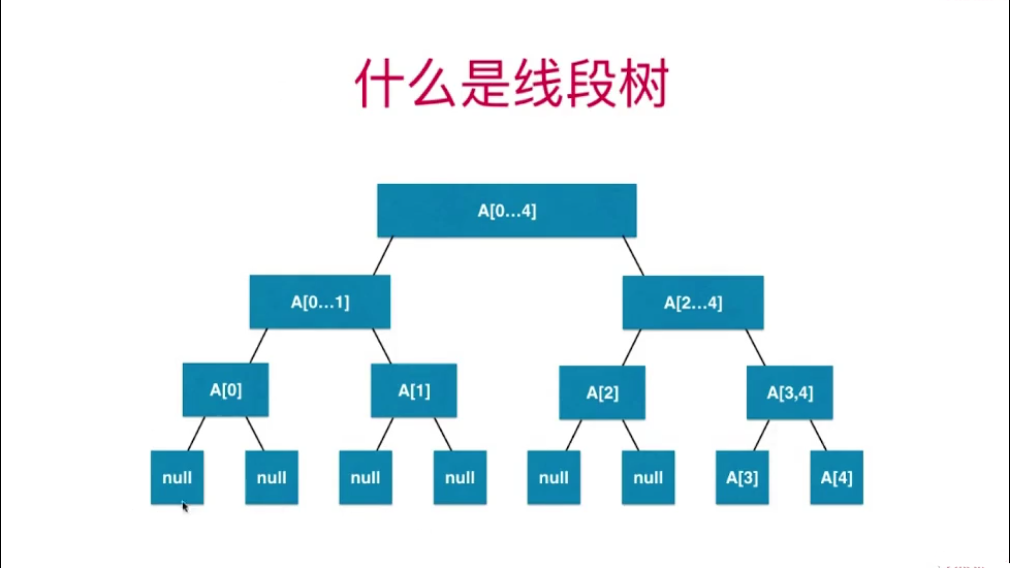
用数组实现线段树:可以将其看做满二叉树,在最后一层,有很多节点是不存在的,那么我们将这些不存在的节点看做是空即可。

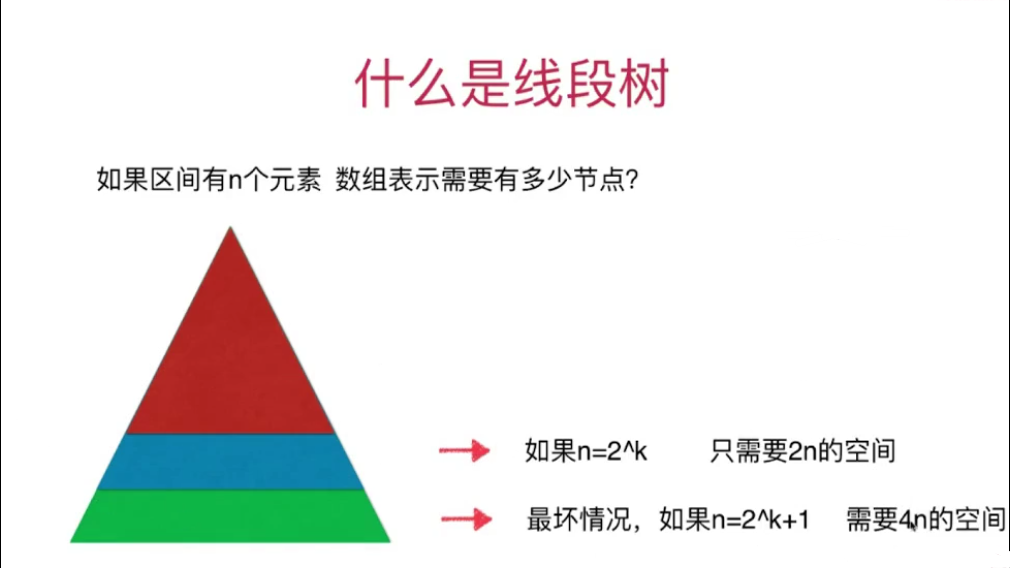
结论:
如果区间有n个元素,数组表示需要有多少个节点?
需要4n的空间。并且线段树不考虑添加元素,即区间固定,区间的大小不会改变,真正改变的是区间中的元素,所以使用静态空间即可。
实现
先写一下线段树的基础代码:
/**
* 线段树
* @author 硝酸铜
* @date 2021/5/24
*/
public class SegmentTree <E>{
/**
* 数组副本
*/
private E[] data;
/**
* 线段树逻辑结构的数组
*/
private E[] tree;
public SegmentTree(E[] arr){
//存储传入数组的副本
this.data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
this.data[i] = arr[i];
}
//4n空间即可存储线段树的所有节点
this.tree = (E[])new Object[4 * arr.length];
//TODO 创建线段树
}
/**
* 根据索引获取元素
* @param index 索引
* @return E
*/
public E get(int index){
if(index < 0 || index > this.data.length){
throw new IllegalArgumentException("Index is illegal.");
}
return this.data[index];
}
/**
* 获取元素个数
* @return int
*/
public int getSize(){
return this.data.length;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子的索引
*
* @param index 索引
* @return int 左孩子的索引
*/
private int leftChild(int index) {
return index * 2 + 1;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子的索引
*
* @param index 索引
* @return int 右孩子的索引
*/
private int rightChild(int index) {
return index * 2 + 2;
}
}
创建线段树
学习了前面的数据结构,线段树的创建也就不难了,这是一个非常典型的递归逻辑。
线段树中,根节点存储的信息,是其两个孩子存储的信息的综合,那么怎么综合,是以业务逻辑来定的:
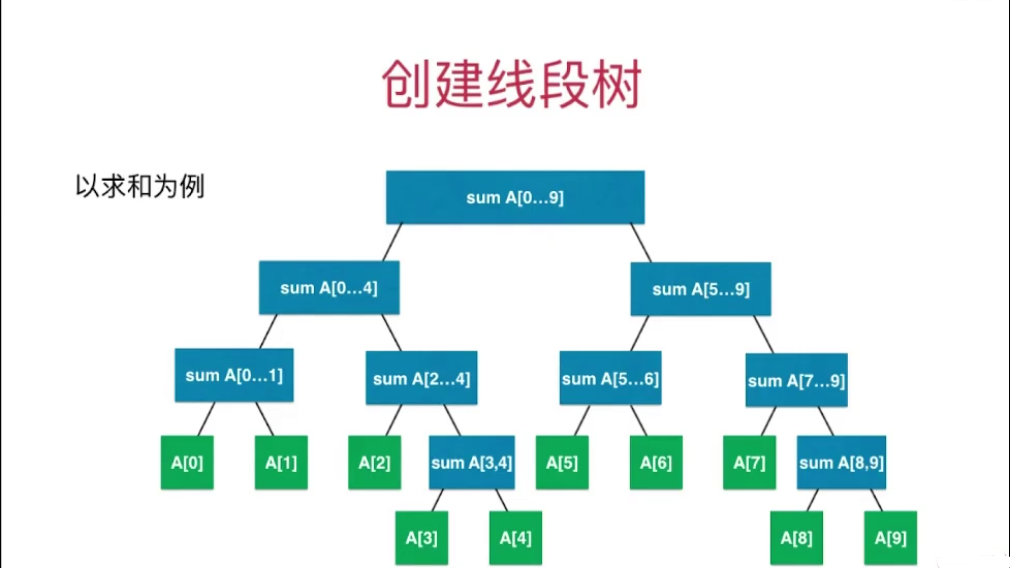
我们想要创建这个线段树的根,那么我们首先需要创建好线段树的两个孩子节点。我们有了两个子树的根节点之后,只需要对孩子节点进行一个综合,这个线段树的根节点就创建好了。对于这两棵子树的创建也是如此。以此类推,递归到底,也就是其区间不能再划分了,也就是最基本的问题,非常典型的递归逻辑
在实现创建线段树逻辑之前,我们要思考一个问题:线段树的综合是根据业务逻辑来执行的,用户在使用线段树的时候,其业务逻辑也会多种多样,我们不能将其具体化,只能抽象化,由用户自己来定义其业务逻辑是怎么样的,该怎么做呢?
其实答案很简单,我们定义一个融合器接口,在创建线段树时,调用其方法即可,至于接口中的方法是怎么实现的,就由用户来关心了。
/**
* 融合器
* @author 硝酸铜
* @date 2021/5/24
*/
public interface Merger<E> {
E merge(E a,E b);
}
public class SegmentTree <E>{
...
/**
* 融合器,定义好了两个区间是如何融合的
*/
private Merger<E> merger;
public SegmentTree(E[] arr,Merger<E> merger){
//存储传入数组的副本
this.data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
this.data[i] = arr[i];
}
//4n空间即可存储线段树的所有节点
this.tree = (E[])new Object[4 * arr.length];
this.merger = merger;
//创建线段树
buildSegmentTree(0,0,data.length - 1);
}
...
/**
* 递归函数
* 宏观语义:在treeIndex的位置创建表示区间[l..r]的线段树
* @param treeIndex 根节点的索引
* @param l 区间左
* @param r 区间右
*/
private void buildSegmentTree(int treeIndex, int l ,int r){
//最基本的问题,区间长度为1,存储的是元素本身
if(r == l){
tree[treeIndex] = data [l];
return;
}
//左右子树的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//计算左右子树的区间: [l,mid];[mid + 1,r]
//同等于 (l + r)/2 ,但是以下方法避免了 l + r 大于int范围的情况
int mid = l + (r - l) / 2;
//先创建左右子树
buildSegmentTree(leftTreeIndex,l,mid);
buildSegmentTree(rightTreeIndex,mid + 1,r);
//再创建根节点,综合两个区间的值
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append('[');
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null) {
res.append(tree[i]);
}
else {
res.append("null");
}
if (i != tree.length - 1) {
res.append(",");
}
}
res.append(']');
return res.toString();
}
}
测试:
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
/*
SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, new Merger<Integer>() {
@Override
public Integer merge(Integer a, Integer b) {
//定义线段树每一个区间a,b实现什么融合,这里是区间的数相加起来
return a>b?a:b;
}
});
*/
//使用lambda表达式返回区间的累加和
SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, Integer::sum);
//使用lambda表达式返回区间的最大值
SegmentTree<Integer> segmentTree1 = new SegmentTree<>(nums, (a, b) -> a > b ? a : b);
System.out.println("每个区间的累加和:" + segmentTree);
System.out.println("每个区间的最大值;" + segmentTree1);
}
>>
/**
-2,0,3,-5,-2,-1 n表示null
/ \ / \
-2,0 3 -5,2 -1
/ \ /\ / \ / \
-2 0 n n -5 2 n n
/ \ / \
n n n n
merger怎么定义,就定义每一个区间实现什么功能,上面下面实现的是累加功能
**/
每个区间的累加和:[-3,1,-4,-2,3,-3,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
每个区间的最大值;[3,3,2,0,3,2,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
线段树中的查询
我们在定义线段树时,对其子树进行划分的时候,是从区间的中间进行划分的,也就是说我们是知道区间是怎么划的。在查询的时候,我们就根据需要查询的区间是不是当前节点的子区间去寻找,比如:
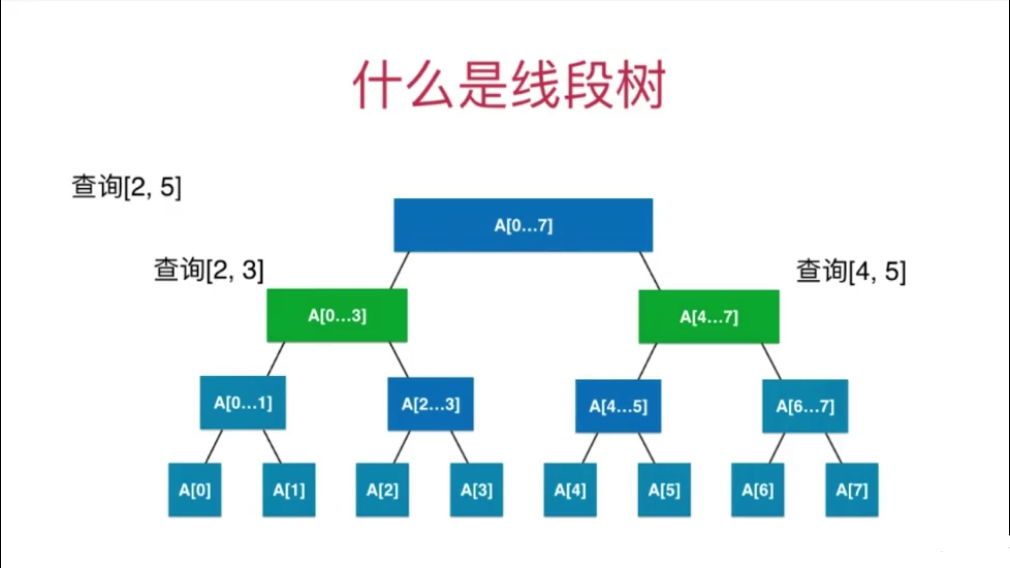
查询区间为[2,5]的值,其是区间[0,7]的子区间,需要去子树中寻找,又因为我们是知道区间是从中间开始划分的,所以将区间[2,5]分为[2,3]和[4,5],然后在当前节点的左右子树中去查询。
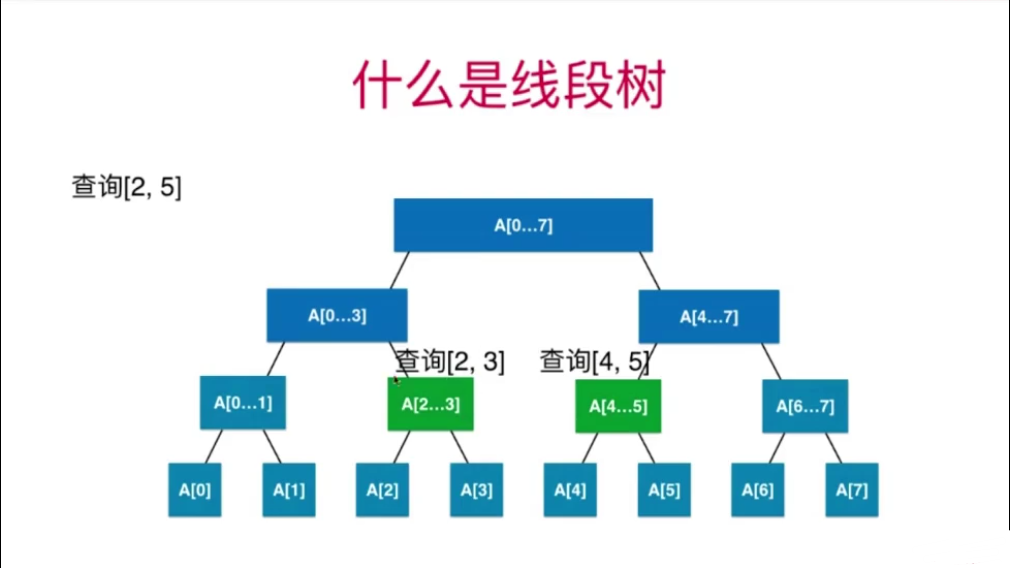
在子树中,区间[2,3]是区间[0,3]的子区间,所以去其子树查询,又因为左孩子[0,1]区间跟其没有关系,所以去右孩子中查询,恰好右孩子正是我们要查询的区间,就不需要继续递归了,返回当前节点的值和另一边的结果综合起来即可,另一边同理。
可以看到,我们不需要从头到尾遍历元素,只需要在线段树中递归即可,只和线段树的高度有关,与区间的长度无关。线段树的高度是logn这个级别的,所以线段树的查询也是logn级别的。
/**
* 返回[queryL,queryR]的值
* @param queryL 查询区间的左边
* @param queryR 查询区间的右边
* @return E 节点
*/
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length ||
queryL > queryR) {
throw new IllegalArgumentException("Index is illegal.");
}
return query(0,0, data.length - 1,queryL,queryR) ;
}
/**
* 递归函数
* 宏观语义:在以treeIndex为根的线段树中[l..r]的范围里,搜索区间[queryL..queryR]的值
* @param treeIndex 根节点的索引
* @param l 区间左边
* @param r 区间右边
* @param queryL 查询区间的左边
* @param queryR 查询区间的右边
* @return E 节点
*/
private E query(int treeIndex,int l,int r,int queryL, int queryR){
//最基本的问题:当两边边界和查询边界相等
if(l == queryL && r == queryR){
return tree[treeIndex];
}
//计算左右子树的区间: [l,mid];[mid + 1,r]
//同等于 (l + r)/2 ,但是以下方法避免了 l + r 大于int范围的情况
int mid = l + (r - l) / 2;
//左右子树的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(queryL >= mid + 1){
//区间在右孩子中
return query(rightTreeIndex,mid + 1,r,queryL,queryR);
}else if(queryR <= mid){
//区间在左孩子中
return query(leftTreeIndex,l,mid,queryL,queryR);
}else {
//区间有一部分在左孩子中,另外一部分在右孩子中,需要在两边查找
//从左孩子中查找
E leftResult = query(leftTreeIndex,l,mid,queryL,mid);
//从右孩子中查找
E rightResut = query(rightTreeIndex,mid + 1,r,mid + 1,queryR);
//融合
return merger.merge(leftResult,rightResut);
}
}
测试
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
/*
SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, new Merger<Integer>() {
@Override
public Integer merge(Integer a, Integer b) {
//定义线段树每一个区间a,b实现什么融合,这里是区间的数相加起来
return a>b?a:b;
}
});
*/
//使用lambda表达式返回区间的累加和
SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, Integer::sum);
//使用lambda表达式返回区间的最大值
SegmentTree<Integer> segmentTree1 = new SegmentTree<>(nums, (a, b) -> a > b ? a : b);
System.out.println("每个区间的累加和:" + segmentTree);
System.out.println("每个区间的最大值;" + segmentTree1);
//查询操作,查询[0,2]区间的和
int sum=segmentTree.query(0,2);
//查询操作,查询[1,3]区间的最大值
int maxNum=segmentTree1.query(1,3);
System.out.println("这个区间的和是:"+sum);
System.out.println("[1,3]这个区间的最大值是:"+maxNum);
}
>>
/**
-2,0,3,-5,-2,-1 n:null
/ \ / \
-2,0 3 -5,2 -1
/ \ /\ / \ / \
-2 0 n n -5 2 n n
/ \ / \
n n n n
merger怎么定义,就定义每一个区间实现什么功能,上面下面实现的是累加功能
**/
每个区间的累加和:[-3,1,-4,-2,3,-3,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
每个区间的最大值;[3,3,2,0,3,2,-1,-2,0,null,null,-5,2,null,null,null,null,null,null,null,null,null,null,null]
这个区间的和是:1
这个区间的最大值是:3
更新
/**
* 将index位置的值,更新为e
* @param index 索引
* @param e 新值
*/
public void set(int index,E e){
if (index < 0 || index > this.data.length) {
throw new IllegalArgumentException("Index is illegal.");
}
this.data[index] = e;
//更新tree
set(0,0,data.length - 1,index,e);
}
/**
* 递归函数
* 宏观语义:在以treeIndex为根的线段树中[l..r]的范围里,更新index的值为e
* @param treeIndex 根索引
* @param l 区间左边
* @param r 区间右边
* @param index 索引
* @param e 新值
*/
private void set(int treeIndex,int l,int r,int index,E e){
//最基本的问题
if(l == r){
//找到了要更新位置
tree[treeIndex] = e;
return;
}
//寻找index这个位置的叶子节点
//计算左右子树的区间: [l,mid];[mid + 1,r]
//同等于 (l + r)/2 ,但是以下方法避免了 l + r 大于int范围的情况
int mid = l + (r - l) / 2;
//左右子树的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(index >= mid + 1){
//往右子树中去更新
set(rightTreeIndex,mid + 1,r,index,e);
}else {
//往左子树中去更新
set(leftTreeIndex,l,mid,index,e);
}
//更新完成,返回的时候,涉及到的路径上的节点的值也需要改变
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}
LeetCode上线段树相关的问题
303.区域和检索 - 数组不可变
给定一个整数数组 nums,求出数组从索引 i 到 j(i ≤ j)范围内元素的总和,包含i、j 两点。
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums从索引i到j(i ≤ j)范围内元素的总和,包含i、j两点(也就是sum(nums[i], nums[i + 1], ... , nums[j]))
示例:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
提示:
0 <= nums.length <= 104-105 <= nums[i] <= 1050 <= i <= j < nums.length- 最多调用 104 次
sumRange方法
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/range-sum-query-immutable
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题模板:
class NumArray {
public NumArray(int[] nums) {
}
public int sumRange(int left, int right) {
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* int param_1 = obj.sumRange(left,right);
*/
思路:没有思路,我们实现的线段树就有这样的功能,直接用即可
/**
* LeetCode 303.区域和检索-数组不可变
* 使用线段树
* @author 硝酸铜
* @date 2021/5/24
*/
public class NumArray {
private SegmentTree<Integer> segmentTree;
public NumArray(int[] nums) {
if(nums.length > 0){
Integer[] data = new Integer[nums.length];
for (int i = 0; i < data.length; i++) {
data[i] = nums[i];
}
segmentTree = new SegmentTree<>(data,Integer::sum);
}
}
public int sumRange(int left, int right) {
if(segmentTree == null){
throw new IllegalArgumentException("Segment Tree is null.");
}
return segmentTree.query(left,right);
}
}
这个问题关心的是线段的和,但是由于数组是不可变的,其实不使用线段树甚至可以获得更好的解答:
不使用线段树的解题思路:
这个问题是求一个区间的所有元素的和,并且这个区间中所有的元素是永远不会改变的,对于这样的需求,其实最自然的想法是进行一个预处理,通过预处理,在求区间元素和的时候,不需要将区间中所有的元素都扫描一遍。这里最典型的预处理就是用一个数组来存储前i个元素的和:
/**
* LeetCode 303.区域和检索-数组不可变
* 不使用线段树
* @author 硝酸铜
* @date 2021/5/24
*/
public class NumArray2 {
/**
* sum[i]存储前i个元素的和,sum[0] = 0
* sum[i]存储nums[0...i-1]的和
*/
private int[] sum;
public NumArray2(int[] nums) {
sum = new int[nums.length + 1];
sum[0] = 0;
for (int i = 1; i < sum.length; i++) {
sum[i] = sum[i - 1] + nums[i - 1];
}
}
public int sumRange(int left, int right) {
return sum[right + 1] - sum[left];
}
}
这种解法既简单又高效,时间复杂度只有O(1)
因为元素不可变,所以不涉及更新操作,那么我们可以使用这种方式来解题。
线段树主要的应用场景还是在动态的情况下
为了和这个问题做一个比较,我们来看一下另一个问题
307.区域和检索-数组可修改
给你一个数组 nums ,请你完成两类查询,其中一类查询要求更新数组下标对应的值,另一类查询要求返回数组中某个范围内元素的总和。
实现 NumArray 类:
NumArray(int[] nums)用整数数组nums初始化对象void update(int index, int val)将nums[index]的值更新为valint sumRange(int left, int right)返回子数组nums[left, right]的总和(即,nums[left] + nums[left + 1], ..., nums[right])
示例:
输入:
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出:
[null, 9, null, 8]解释:
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 9 ,sum([1,3,5]) = 9
numArray.update(1, 2); // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 8 ,sum([1,2,5]) = 8
提示:
1 <= nums.length <= 3 * 104-100 <= nums[i] <= 1000 <= index < nums.length-100 <= val <= 1000 <= left <= right < nums.length
最多调用 3 * 104 次update和sumRange方法
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/range-sum-query-mutable
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题模板:
class NumArray {
public NumArray(int[] nums) {
}
public void update(int index, int val) {
}
public int sumRange(int left, int right) {
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(index,val);
* int param_2 = obj.sumRange(left,right);
*/
思路:这里因为涉及到了元素的更新,是动态的,所以需要用到线段树。但是如果我们不使用线段树,而是使用解决303号问题中,非线段树的方式,对其进行一下修改,有没有问题呢?
我们来简单分析一下,使用非线段树方式怎么实现update: 当我们update一个位置的元素之后,其整个预处理数组sum都会发生变化,相应的,我们也得update整个sum数组
/**
* LeetCode 307.区域和检索-数组可变
* 不使用线段树
* @author 硝酸铜
* @date 2021/5/24
*/
public class NumArray3 {
/**
* sum[i]存储前i个元素的和,sum[0] = 0
* sum[i]存储nums[0...i-1]的和
*/
private int[] sum;
/**
* 数组的副本
*/
private int[] data;
public NumArray3(int[] nums) {
data = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
data[i] = nums[i];
}
sum = new int[nums.length + 1];
sum[0] = 0;
for (int i = 1; i < sum.length; i++) {
sum[i] = sum[i - 1] + nums[i - 1];
}
}
public void update(int i, int val){
data[i] = val;
for (int index = i + 1; index < sum.length; index++) {
sum[index] = sum[index - 1] + data[index - 1];
}
}
public int sumRange(int left, int right) {
return sum[right + 1] - sum[left];
}
}
这样的实现,更新操作的时间复杂度为O(n)
当我们将解答放入LeetCode中提交之后,出现:
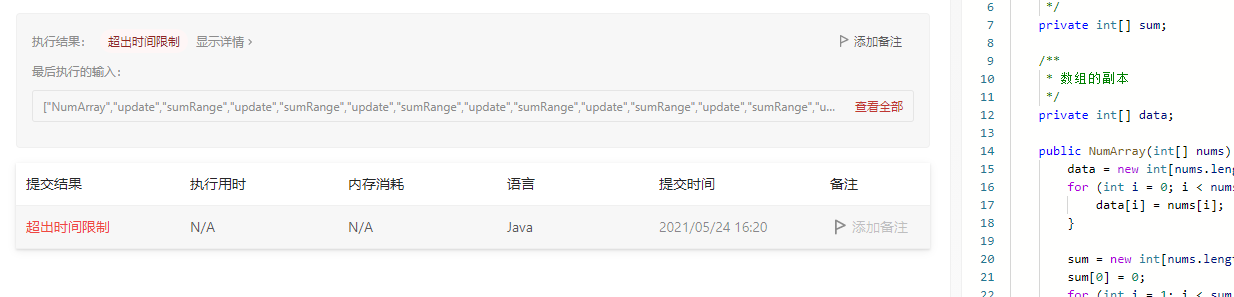
也就是说,这种解答方式性能太差了,超过了问题运行的时间,更新操作时间复杂度为O(n),如果操作M次更新,则需要M * n 这个级别的,太慢了。
这个时候,线段树就很必要了。
/**
* LeetCode 307.区域和检索-数组可修改
* 使用线段树
* @author 硝酸铜
* @date 2021/5/24
*/
public class NumArray4 {
private SegmentTree<Integer> segmentTree;
public NumArray4(int[] nums) {
if(nums.length > 0){
Integer[] data = new Integer[nums.length];
for (int i = 0; i < data.length; i++) {
data[i] = nums[i];
}
segmentTree = new SegmentTree<>(data,Integer::sum);
}
}
public void update(int index,int val){
if(segmentTree == null){
throw new IllegalArgumentException("Segment Tree is null.");
}
segmentTree.set(index,val);
}
public int sumRange(int left, int right) {
if(segmentTree == null){
throw new IllegalArgumentException("Segment Tree is null.");
}
return segmentTree.query(left,right);
}
}
这里就可以看到线段树的威力了,其构造,更新和查询都是O(logn)级别的,对于M的操作来说,是M * logn级别的,是远远的快于M * n 这个级别的。
时间复杂度
- 新建 O(4n) = O(n)
- 更新 O(logn)
- 查询 O(logn)
对于要考虑区间这种数据,尤其是查询区间的统计信息,同时数据是动态的,不时地还需要更新的情况下,线段树就很有用了。


