7,优先队列和堆
《玩转数据结构》-liuyubobobo 课程笔记
树这种数据结构是计算机科学领域较为重要的数据结构,因为其扩展性强,除了二分搜索树,二叉树之外,还有许多种结构,从这一章开始,我们来学习其他四种新的树形结构,体会数据结构的灵活性
在介绍树形结构堆之前,我们来了解一下更加高层的概念:优先队列
优先队列介绍
本身是一种队列
普通队列:先进先出
优先队列:出队顺序与入队顺序无关,和优先级相关
常见的场景:
操作系统中对任务调度,操作系统同一时间会对多个任务进行调度,分配计算资源。操作系统会动态选择优先级最高的任务执行。
这里的动态是操作系统不知道一共有多少个任务(因为在随着时间推移,任务数量会不断地增加),操作系统会更加新来的任务,调整整个队列的优先级。
由此可见,优先队列的关键词其实不是优先,而是动态
优先队列本质上其实就是队列,所以其接口也和队列一样
Queue<E>
- void enqueue(E) 入队列
- E dequeue() 出队列
- E getFront() 获取队首的元素
- int getSize()
- boolean isEmpty()
其实现之后,功能会有区别,其出队和获取队首元素应该是优先级最高的元素。
其也可以使用底层数据结构实现
普通线性结构: 入队O(1),出队O(n) 因为每次出队都需要去寻找最大的元素,所以都需要遍历一次,太慢
顺序线性结构: 入队O(n),出队O(1), 维持从小到大或者从大到小的顺序线性结构,出队简单了,但是入队的时候需要进行遍历判断,去寻找存储的位置。
线性结构有自己的劣势,不管是普通的还是顺序的,时间复杂度都有O(n)的情况
堆: 入队O(logn) 出队O(logn)更为高效的底层实现,前面我们经过试验,得到O(logn)是很高效的,使用这种数据结构实现的优先队列效率高效。
那么什么是堆呢?
下面我们来学习一下
堆
在计算机科学领域,如果一个数据结构的时间复杂度为O(logn),那么其多半都和树有关,不一定是显示的一棵树,也可能是使用递归形成的隐形的递归树。
一个堆其本身也是一棵树,其多种多样,我们这里学习一下主流的,使用二叉树来实现一个堆,通常被称为二叉堆
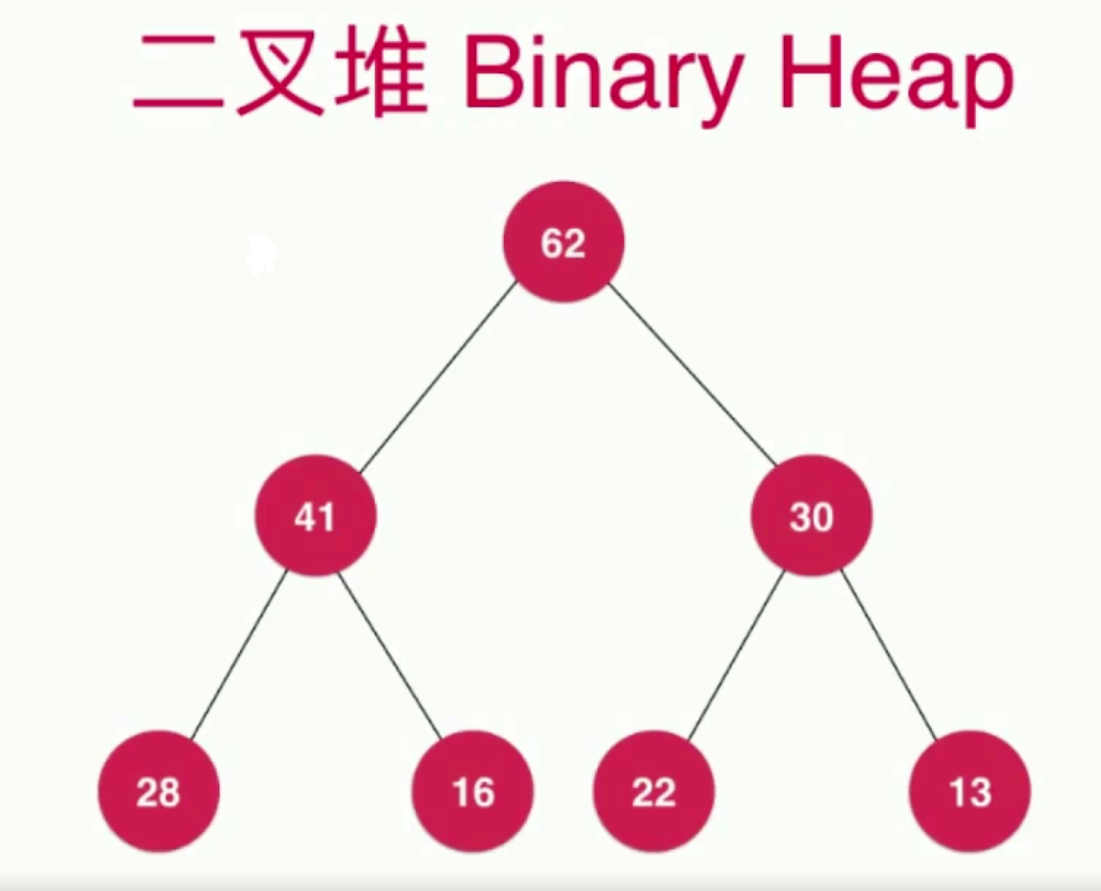
说白了,二叉堆就是满足一些特殊性质的二叉树:
-
完全二叉树
对于整棵树来说,元素排列的顺序是一层一层的,从左到右的排列。最下面一层必定是叶子节点,上面一层可能还有叶子节点,但这些叶子节点一定全部在这棵树的右侧
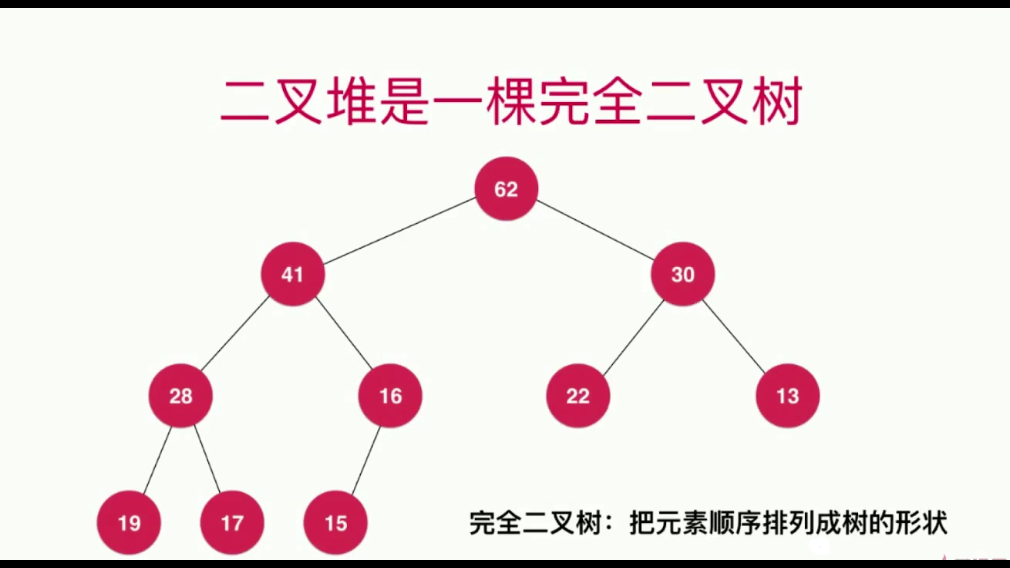
-
所有的节点值都大于或者等于其孩子节点的值(最大堆)
-
所有的节点值都小于或者等于其孩子节点的值(最小堆)
ps:节点大小与节点层次之间没有关系,比如层数为4的值为19是大于层数为3的值16的
-
可以用数组存储二叉堆
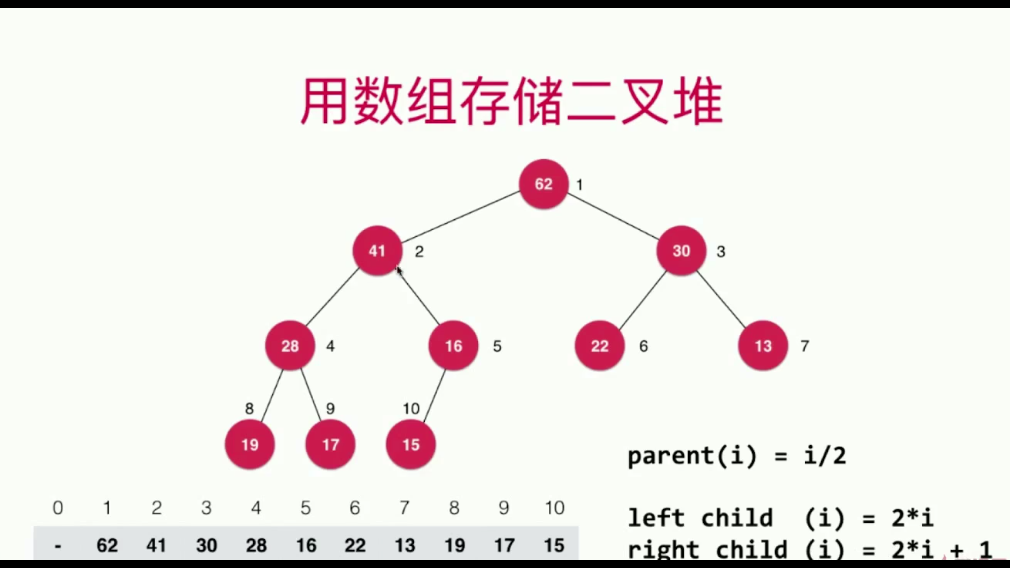
如图,其索引计算:左孩子索引为节点索引的2倍,右孩子为节点索引的2倍加1
如果不想空出索引为0的位置,也可以这样:
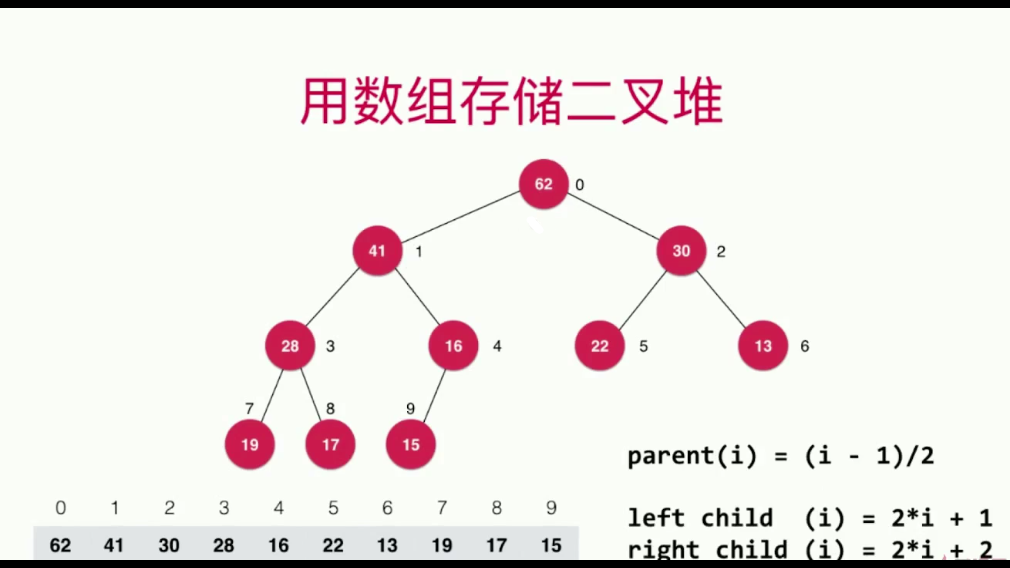
在计算索引的时候,对索引进行偏移即可
最大堆实现
先写出基本的内容,使用我们之前实现的动态数组来存储二叉堆
import com.cupricnitrate.datastructure.MyArray;
/**
* 最大堆
* @author 硝酸铜
* @date 2021/5/20
*/
public class MaxHeap<E extends Comparable<E>> {
/**
* 使用数组来存储
*/
private MyArray<E> data;
public MaxHeap(int capacity){
this.data = new MyArray<>(capacity);
}
public MaxHeap(){
this.data = new MyArray<>();
}
/**
* 获取元素个数
* @return int 元素个数
*/
public int size(){
return this.data.getSize();
}
/**
* 判断堆是否为空
* @return boolean
*/
public boolean isEmpty(){
return this.data.isEmpty();
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的父节点的索引
* @param index 索引
* @return int 父节点的索引
*/
private int parent(int index){
//根节点没有父节点
if(index == 0){
throw new IllegalArgumentException("index-0 doesn't have parent.")
}
return (index -1)/2;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子的索引
* @param index 索引
* @return int 左孩子的索引
*/
private int leftChild(int index){
return index * 2 + 1;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子的索引
* @param index 索引
* @return int 右孩子的索引
*/
private int rightChild(int index){
return index * 2 + 2;
}
}
向堆中添加元素和Sift Up
在用户的角度来说,添加操作就是向堆中添加一个元素,但是在堆的角度来说,涉及到一个基础的内部操作:Sift Up,即堆中元素的上浮的过程
比如说这里我们要将52添加进堆中:
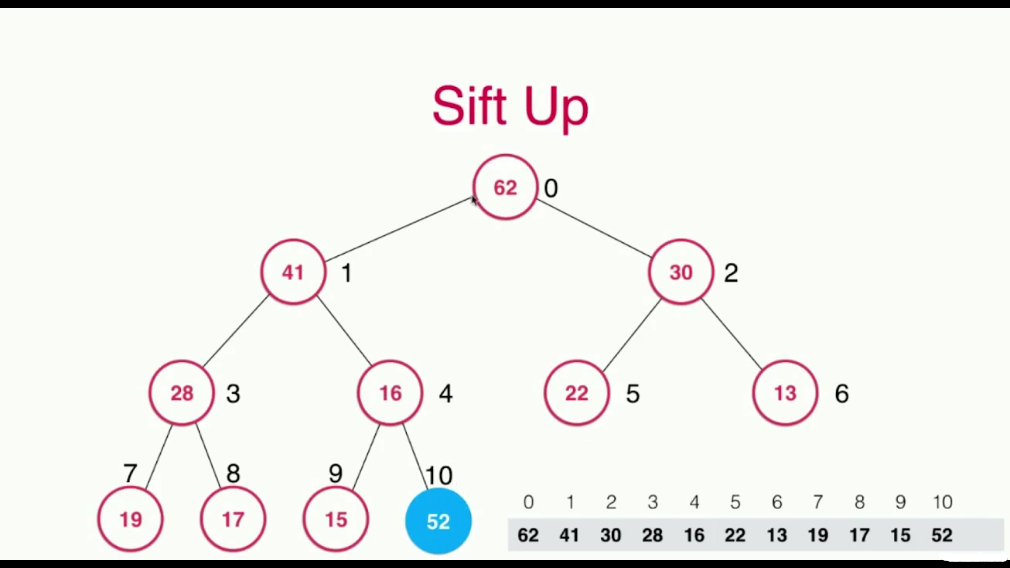
这里将元素52添加进堆中之后,为了满足堆得性质,还需要进行一些调整,需要堆元素52的父节点(们)进行调整。从52开始,依次将其与其父亲节点,爷爷节点...进行比较,不满足堆的性质(父节点大于孩子节点)则交换,直到其满足堆得性质为止:
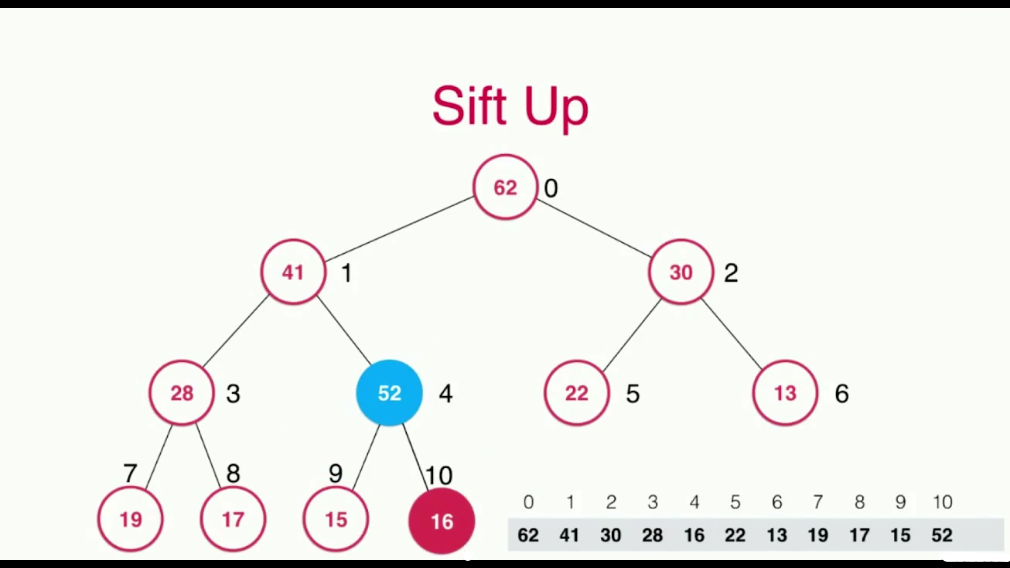

最终得到的是满足堆性质的数据结构,这个过程就叫做Sift Up,元素上浮的过程
我们接下来使用代码来实现这个过程
/**
* 向堆中添加元素
* @param e 元素
*/
public void add(E e){
//先在数组中添加这个元素
this.data.addLast(e);
//Sift Up
this.siftUp(this.data.getSize() - 1);
}
/**
* 元素上浮
* @param k 元素的索引
*/
private void siftUp(int k){
//当k大于0,其父亲节点小于当前节点的时候,进行上浮操作
while (k > 0 && data.get(this.parent(k)).compareTo(data.get(k)) < 0){
//将父亲节点和当前节点进行交换
this.swap(k,this.parent(k));
//继续与其父节点比较,直到满足堆的性质为止
k = this.parent(k);
}
}
/**
* 交换索引为i,j位置的元素
* @param i 索引
* @param j 索引
*/
private void swap(int i ,int j){
if( i < 0 || i >= data.getSize() || j < 0 || j >= data.getSize()){
throw new IllegalArgumentException("Index is illegal.");
}
E shift = this.data.get(i);
this.data.set(i,this.data.get(j));
this.data.set(j,shift);
}
取出堆中的元素和Sift Down
在堆中,取出操作只能取出最大的那个元素
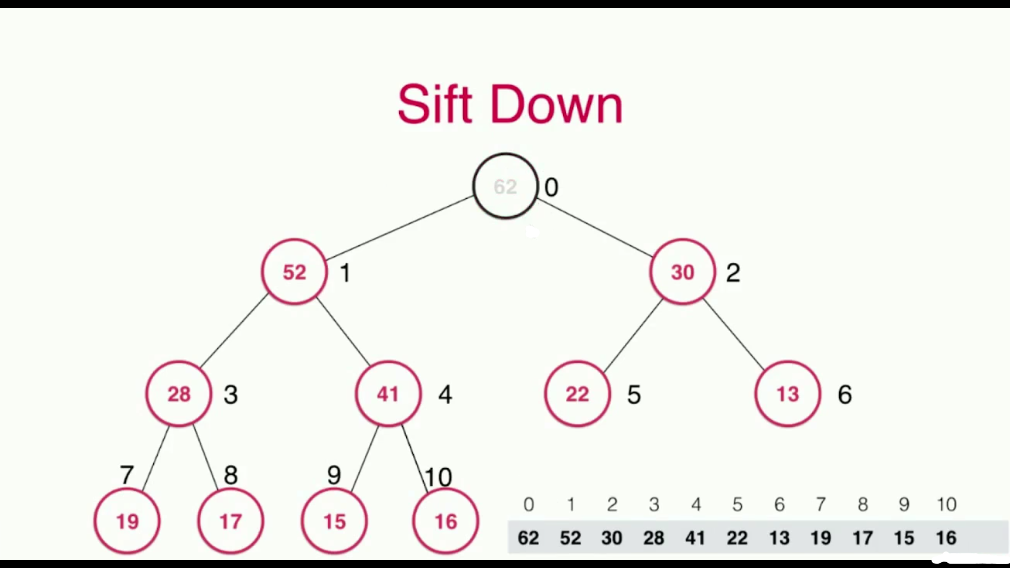
当我们把最大的元素,也就是根节点取出去之后,对于堆来说,剩下了两棵子树,将两棵子树合并成一棵树相对比较复杂,所以我们使用了一个小技巧,就是将堆中最末的那个元素,顶到堆顶位置,然后进行调整即可,这个过程就叫做Sift Down,数据的下沉
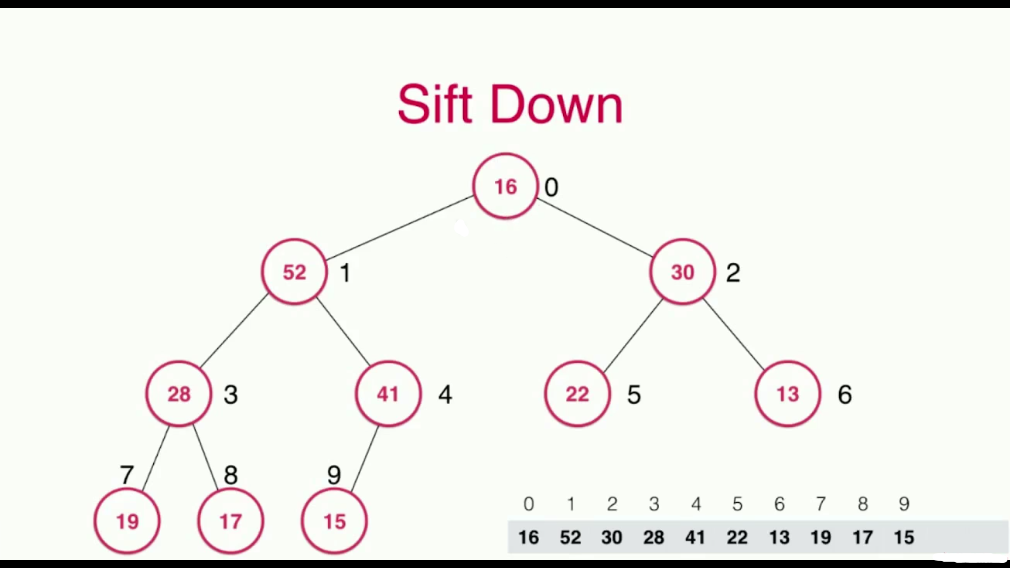
每次调整,与其两个孩子比较,选择比自己大的并且是最大的那个孩子进行交换
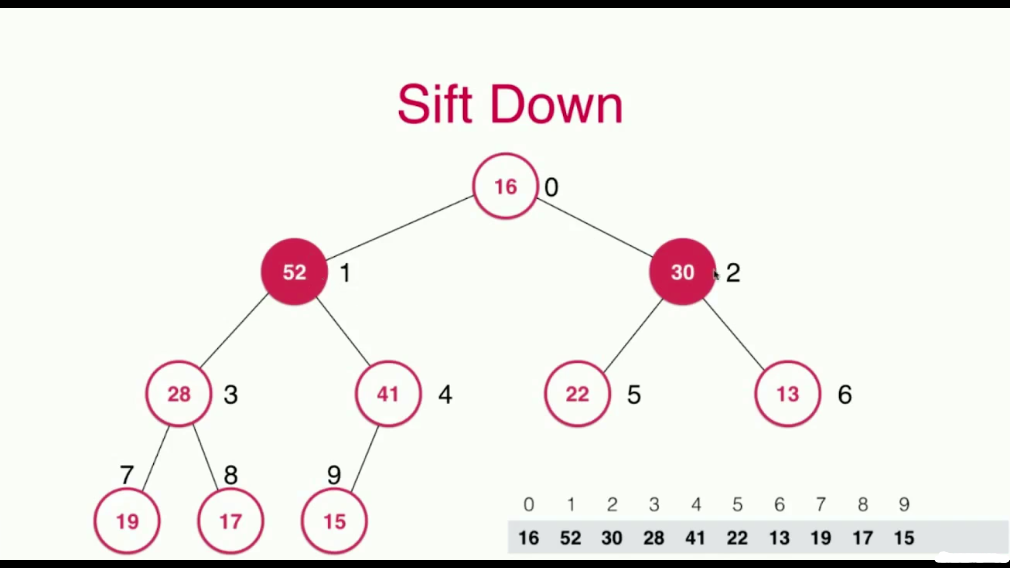
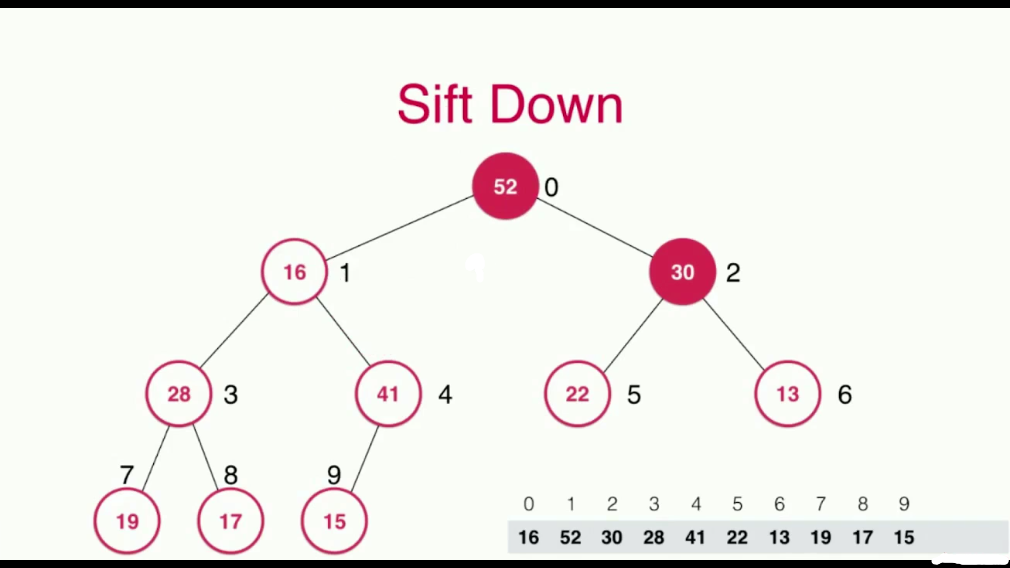
依次比较,直到满足堆的性质,即节点值都大于或者等于其孩子节点的值
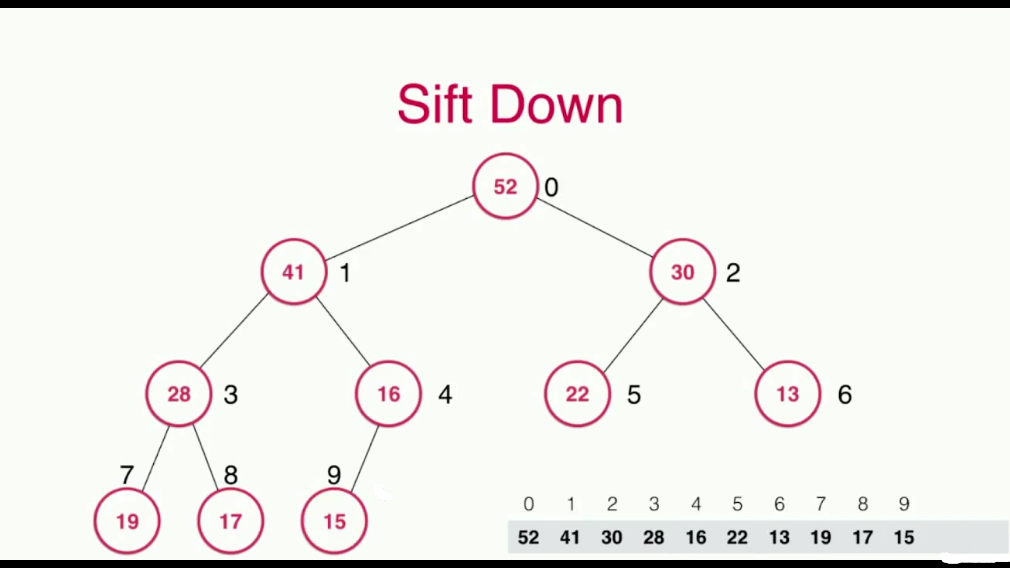
下面我们使用代码实现这个过程
/**
* 取出最大元素
* @return 最大元素
*/
public E extractMax(){
E ret = this.findMax();
//将堆未中的元素推到堆顶
this.swap(0,data.getSize() - 1);
this.data.removeLast();
//siftDown
this.siftDown(0);
return ret;
}
/**
* 元素下沉
* @param k 元素的索引
*/
private void siftDown(int k){
//当元素的左孩子索引大于元素个数的时候,说明其已经是叶子节点了,则中止循环
while (leftChild(k) < data.getSize()){
//进入循环,说明左孩子存在
int l = leftChild(k);
//j保存的是左孩子和右孩子中,最大值的索引
int j = l;
//如果右孩子存在,并且右孩子大于左孩子,则l保存的就为右孩子索引
if( l + 1 < data.getSize() && data.get(l + 1).compareTo(data.get(l)) > 0){
j = rightChild(k);
}
if(data.get(k).compareTo(data.get(j)) >= 0){
//根节点大于或等于左右孩子中的最大值,说明下沉结束了
break;
}
else {
//否则交换k与l的索引位置,继续下沉
this.swap(k,j);
k = j;
}
}
}
测试
我们来测试一下
public static void main(String[] args) {
//操作数量
int n = 1000000;
MaxHeap<Integer> maxHeap = new MaxHeap<>();
Random random = new Random();
for (int i = 0; i < n; i++) {
maxHeap.add(random.nextInt(Integer.MAX_VALUE));
}
//验证每次取出的都是最大值
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = maxHeap.extractMax();
}
for (int i = 1; i < n; i++) {
//如果前一个小于后一个,说明排序错误
if(arr[i-1] < arr[i] ){
throw new IllegalArgumentException("Error");
}
}
//没有抛出异常,说明成功
System.out.println("Test MaxHeap completed.");
}
>>
Test MaxHeap completed.
复杂度分析
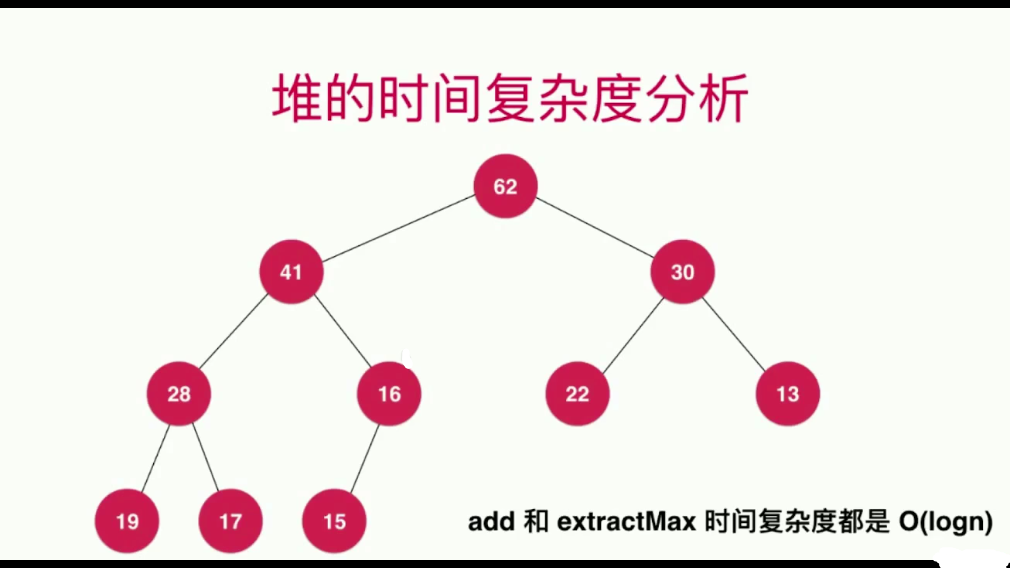
因为堆是完全二叉树,所以其不会退化成链表,也就是说其时间复杂度永远是O(logn)非常高效
Replace
取出最大元素后,放入一个新的元素。
- 实现:可以先 extraMax,再 add,两次 O(logn)的操作
- 实现:可以直接将堆顶元素替换以后 Sift Down,一次 O(logn)的操作
/**
* 取出堆中的最大元素,并且替换成元素 e
* @param e 元素
* @return 堆中最大的元素
*/
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
Heapify
将任意数组整理成堆的形状。将当前数组看成一个完全二叉树,这个例子中,对于这个数组并不是一个堆,不满足堆的性质。
但是我们同样可以把它看成一棵完全二叉树,对于这个完全二叉树,我们从最后一个非叶子节点开始计算,如下图所示有五个叶子节点:
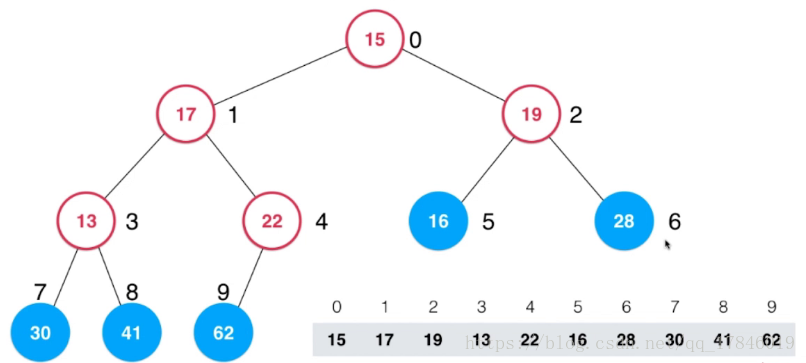
最后一个非叶子节点就是 22 这个元素所在的节点,从这个节点开始倒着从后向前不断的 Sift Down 就可以了。
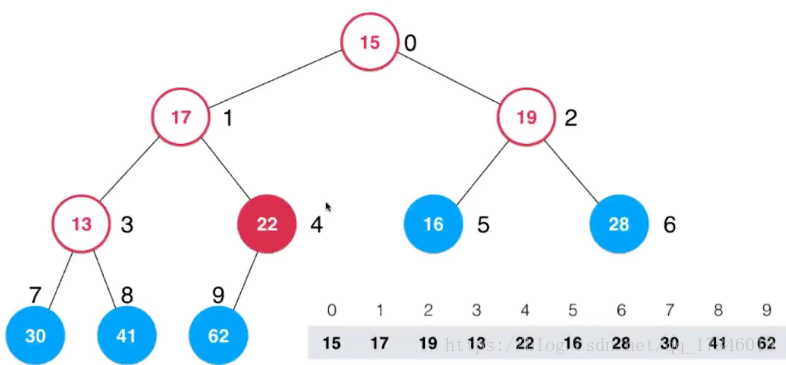
首先有一个非常重要的问题,就是我们如何定位最后一个非叶子节点所处的索引是多少?
- 从最后一个非叶子节点开始计算(如何获得节点?答:拿到最后一个节点,然后拿到他的父亲节点)
- 比如最后一个节点size-1,name它的父亲节点(最后一个非叶子节点)为:parent(size-1)
找到它父亲节点,接下来就进行 Sift Down 操作,22 和 62 交换,此时 22 已经是叶子节点了,下沉操作就完成了。
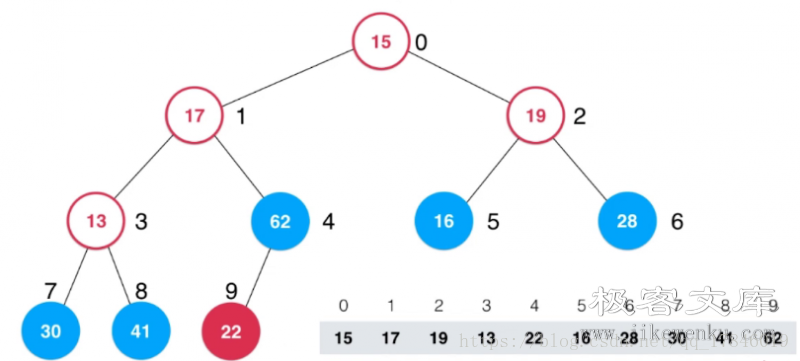
然后看索引为 3 的节点,13 和 41 交换,13 变成叶子节点无法继续下沉。
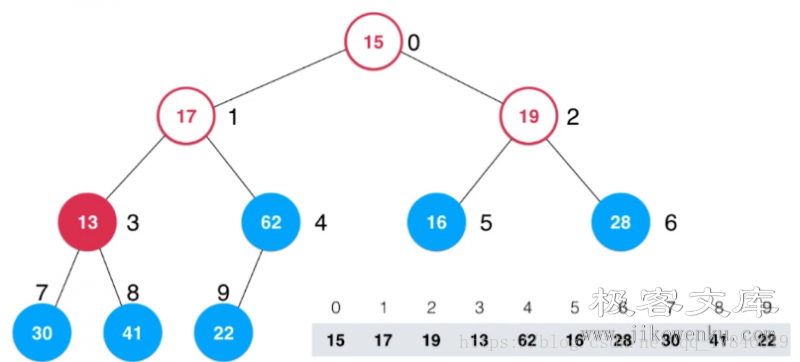
然后接下来依次类推,最终结果如下,建议仔细分析一下操作流程。
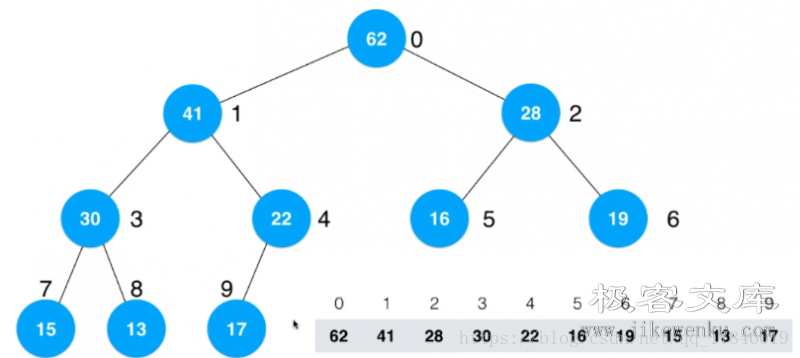
这是整个流程图:
Heapify 的算法复杂度
不使用Heapify的过程:将 n 个元素逐个插入到一个空堆中,算法复杂度是 O(nlogn)
使用 Heapify 的过程,算法复杂度为 O(n)
当n>10时,O(nlogn)>O(n)
实现
/**
* 带参构造,使用Heapify
* @param arr 数组
*/
public MaxHeap(E[] arr) {
data = new MyArray<>(arr);
for (int i = parent(arr.length - 1); i >= 0; i--) {
//从最后一个非叶子节点开始siftDown
siftDown(i);
}
}
测试
public static void main(String[] args) {
int n = 1000000;
Random random = new Random();
Integer[] testData = new Integer[n];
for(int i = 0 ; i < n ; i ++) {
testData[i] = random.nextInt(Integer.MAX_VALUE);
}
double time1 = testHeap(testData, false);
System.out.println("Without heapify: " + time1 + " ms");
double time2 = testHeap(testData, true);
System.out.println("With heapify: " + time2 + " ms");
}
private static double testHeap(Integer[] testData, boolean isHeapify) {
long startTime = System.currentTimeMillis();
MaxHeap<Integer> maxHeap;
//使用Heapify插入元素
if (isHeapify) {
maxHeap = new MaxHeap<>(testData);
}
//不使用Heapify插入元素
else {
maxHeap = new MaxHeap<>();
for (int num : testData) {
maxHeap.add(num);
}
}
//取出元素的操作
int[] arr = new int[testData.length];
for (int i = 0; i < testData.length; i++) {
arr[i] = maxHeap.extractMax();
}
for (int i = 1; i < testData.length; i++) {
if (arr[i - 1] < arr[i]) {
throw new IllegalArgumentException("Error");
}
}
System.out.println("Test MaxHeap completed.");
long endTime = System.currentTimeMillis();
return (endTime - startTime);
}
>>
Test MaxHeap completed.
Without heapify: 855.0 ms
Test MaxHeap completed.
With heapify: 776.0 ms
完整代码
import com.cupricnitrate.datastructure.MyArray;
/**
* 最大堆
*
* @author 硝酸铜
* @date 2021/5/20
*/
public class MaxHeap<E extends Comparable<E>> {
/**
* 使用数组来存储
*/
private MyArray<E> data;
public MaxHeap(int capacity) {
this.data = new MyArray<>(capacity);
}
public MaxHeap() {
this.data = new MyArray<>();
}
/**
* 带参构造,使用Heapify
*
* @param arr 数组
*/
public MaxHeap(E[] arr) {
data = new MyArray<>(arr);
for (int i = parent(arr.length - 1); i >= 0; i--) {
//从最后一个非叶子节点开始siftDown
siftDown(i);
}
}
/**
* 获取元素个数
*
* @return int 元素个数
*/
public int size() {
return this.data.getSize();
}
/**
* 判断堆是否为空
*
* @return boolean
*/
public boolean isEmpty() {
return this.data.isEmpty();
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的父节点的索引
*
* @param index 索引
* @return int 父节点的索引
*/
private int parent(int index) {
//根节点没有父节点
if (index == 0) {
throw new IllegalArgumentException("index-0 doesn't have parent.");
}
return (index - 1) / 2;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子的索引
*
* @param index 索引
* @return int 左孩子的索引
*/
private int leftChild(int index) {
return index * 2 + 1;
}
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子的索引
*
* @param index 索引
* @return int 右孩子的索引
*/
private int rightChild(int index) {
return index * 2 + 2;
}
/**
* 向堆中添加元素
*
* @param e 元素
*/
public void add(E e) {
//先在数组中添加这个元素
this.data.addLast(e);
//Sift Up
this.siftUp(this.data.getSize() - 1);
}
/**
* 元素上浮
*
* @param k 元素的索引
*/
private void siftUp(int k) {
//当k大于0,其父亲节点小于当前节点的时候,进行上浮操作
while (k > 0 && data.get(this.parent(k)).compareTo(data.get(k)) < 0) {
//将父亲节点和当前节点进行交换
this.swap(k, this.parent(k));
//继续与其父节点比较,直到满足堆的性质为止
k = this.parent(k);
}
}
/**
* 交换索引为i,j位置的元素
*
* @param i 索引
* @param j 索引
*/
private void swap(int i, int j) {
if (i < 0 || i >= data.getSize() || j < 0 || j >= data.getSize()) {
throw new IllegalArgumentException("Index is illegal.");
}
E shift = this.data.get(i);
this.data.set(i, this.data.get(j));
this.data.set(j, shift);
}
/**
* 获取堆中最大的元素
*
* @return 最大的元素
*/
public E findMax() {
if (this.data.isEmpty()) {
throw new IllegalArgumentException("Can not findMax when heap is empty!");
}
return data.get(0);
}
/**
* 取出最大元素
*
* @return 最大元素
*/
public E extractMax() {
E ret = this.findMax();
//将堆未中的元素推到堆顶
this.swap(0, data.getSize() - 1);
this.data.removeLast();
//siftDown
this.siftDown(0);
return ret;
}
/**
* 元素下沉
*
* @param k 元素的索引
*/
private void siftDown(int k) {
//当元素的左孩子索引大于元素个数的时候,说明其已经是叶子节点了,则中止循环
while (leftChild(k) < data.getSize()) {
//进入循环,说明左孩子存在
int l = leftChild(k);
//j保存的是左孩子和右孩子中,最大值的索引
int j = l;
//如果右孩子存在,并且右孩子大于左孩子,则l保存的就为右孩子索引
if (l + 1 < data.getSize() && data.get(l + 1).compareTo(data.get(l)) > 0) {
j = rightChild(k);
}
if (data.get(k).compareTo(data.get(j)) >= 0) {
//根节点大于或等于左右孩子中的最大值,说明下沉结束了
break;
} else {
//否则交换k与l的索引位置,继续下沉
this.swap(k, j);
k = j;
}
}
}
/**
* 取出堆中的最大元素,并且替换成元素 e
*
* @param e 元素
* @return 堆中最大的元素
*/
public E replace(E e) {
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
}
优先队列的实现
我们现在已经实现了我们自己的最大堆这样一个数据结构,在学习最大堆的过程中,我们可以发现,使用最大堆来实现优先队列是极其容易的。
因为优先队列本质上还是一个队列,所以我们复用之前的队列接口:
/**
* 队列接口
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/3/23
*/
public interface Queue<E> {
/**
* 入队列
* @param e 元素
*/
void enqueue(E e);
/**
* 出队列
* @return 元素
*/
E dequeue();
/**
* 获取队首元素
* @return 队首元素
*/
E getFront();
/**
* 获取队列中元素数量
* @return 队列中元素数量
*/
int getSize();
/**
* 判断队列是否为空
* @return true/false
*/
boolean isEmpty();
}
实现很简单,堆的接口都能直接使用
import com.cupricnitrate.datastructure.heap.MaxHeap;
/**
* 优先队列
* @author 硝酸铜
* @date 2021/5/21
*/
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
this.maxHeap = new MaxHeap<>();
}
/**
* 入队列
* @param e 元素
*/
@Override
public void enqueue(E e) {
maxHeap.add(e);
}
/**
* 出队列
* @return 元素
*/
@Override
public E dequeue() {
return maxHeap.extractMax();
}
/**
* 获取队首元素,也就是堆中最大的元素
* @return 队首元素
*/
@Override
public E getFront() {
return maxHeap.findMax();
}
/**
* 获取队列中元素数量
* @return 队列中元素数量
*/
@Override
public int getSize() {
return maxHeap.size();
}
/**
* 判断队列是否为空
* @return true/false
*/
@Override
public boolean isEmpty() {
return maxHeap.isEmpty();
}
}
优先队列的经典问题
在 100 0000个元素中选出前100名?
在N个元素总选出前M个元素(N>>M)
如果使用排序(高级的排序方法,比如:归并排序、快速排序等)的时间复杂度:O(NlogN)
使用优先队列——>O(NlogM)
方法:使用一个优先队列,维护当前看到的前M个元素(前M个最大的元素)。
对于N个元素,从头到尾遍历一遍,在遍历的时候,将这N个元素的前M个元素放入一个优先队列中。之后每遍历一个新的元素,对优先队列中最小的元素进行比较,如果这个新的元素大于优先队列中最小的元素,就将其优先队列中最小的元素扔出去,将新的元素增加进优先队列。
可以看到,这里使用的是最小堆,我们之前实现了最大堆,将其改为最小堆也很简单,改一个符号即可。
并且使用最大堆也可以,因为其关键在于优先队列中优先级的定义,没有人规定优先队列中,元素越大,优先级越高,大小是相对的。我们完全可以定义,在优先队列中,元素的值越小,元素的优先级越高,那么使用最大堆也可以解决这个问题。
我们来看一下LeetCode上面具体的类似的问题
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:输入: nums = [1], k = 1
输出: [1]
提示:
- 1 <= nums.length <= 105
- k 的取值范围是 [1, 数组中不相同的元素的个数]
- 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
进阶:你所设计算法的时间复杂度 必须 优于 O(n log n) ,其中 n 是数组大小。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/top-k-frequent-elements
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题模板:
class Solution {
public int[] topKFrequent(int[] nums, int k) {
}
}
解题思路:记录元素出现的频次,使用TreeMap<K,V>来记录
首先,用TreeMap<K,V>来记录每个元素出现的频次
其次,遍历TreeMap中的key键值,如果优先队列没有满,则将这个元素添加到优先队列里面去,如果满了,就判断该元素出现的频次是否比队首频次最低的相比,如果大,则移除队首元素,要这个元素入队(在队尾,会根据频次来实现上浮)。
然后,因为优先队列是基于最小对实现的(最小值在队首),可以利用元素出现的频次来做优先级,频次越小的就放到队首,相对它的优先级就高。
最后,将得到的结果放到ArrayList中返回
我们首先使用我们实现的最大堆来解决这个问题:
import java.util.Arrays;
import java.util.Map;
import java.util.Optional;
import java.util.TreeMap;
/**
* 力扣 347.前 K 个高频元素
* @author 硝酸铜
* @date 2021/5/21
*/
public class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer,Integer> map = new TreeMap<>();
for (int num:nums) {
if (map.containsKey(num)){
//出现过,频次+1
map.put(num,map.get(num) + 1);
}else {
//第一次出现,频次为1
map.put(num,1);
}
}
//求出前K个频次最高的元素
PriorityQueue<Freq> priorityQueue = new PriorityQueue<>();
//遍历映射
map.forEach((key,value) -> {
//先将前K个元素放入优先队列中
if(priorityQueue.getSize() < k){
priorityQueue.enqueue(new Freq(key,value));
}
//已经有K个元素之后,对每个元素与优先级最高的元素进行对比
//如果大于优先级最高的,即大于频次最小的,则优先级最高的出队,新元素入队
else if(value > Optional.ofNullable(priorityQueue.getFront()).orElse(new Freq(0,0)).freq){
priorityQueue.dequeue();
priorityQueue.enqueue(new Freq(key,value));
}
});
//组成返回结果
int[] res = new int[priorityQueue.getSize()];
for (int i = 0; i < res.length; i++) {
res[i] = priorityQueue.dequeue().e;
}
return res;
}
/**
* 频次数据对,关心数组中的元素和频次
*/
private class Freq implements Comparable<Freq>{
/**
* 数据
*/
private int e;
/**
* 频次
*/
private int freq;
public Freq(int e,int freq){
this.e = e;
this.freq = freq;
}
public int getE() {
return e;
}
public int getFreq() {
return freq;
}
public void setE(int e) {
this.e = e;
}
public void setFreq(int freq) {
this.freq = freq;
}
/**
* 定义优先级,什么叫优先级高
* @param o 另一个Freq对象
* @return 1 大于; -1 小于; 0 等于;
*/
@Override
public int compareTo(Freq o) {
//我们使用最大堆来解决这个问题,则需要定义频次越低,优先级越高
if(this.freq < o.freq){
//当前元素频次比另一个元素频次低,则说明优先级高
return 1;
}
if(this.freq > o.freq){
//当前元素频次比另一个元素频次高,则说明优先级低
return -1;
}
else {
//相等
return 0;
}
}
}
}
然后我们使用Java标准库中的优先队列来解决这个问题,注意,Java标准库中的优先队列是最小堆!
和堆相关的更多话题和广义队列
d叉堆:有d个孩子的堆,也满足完全二叉树
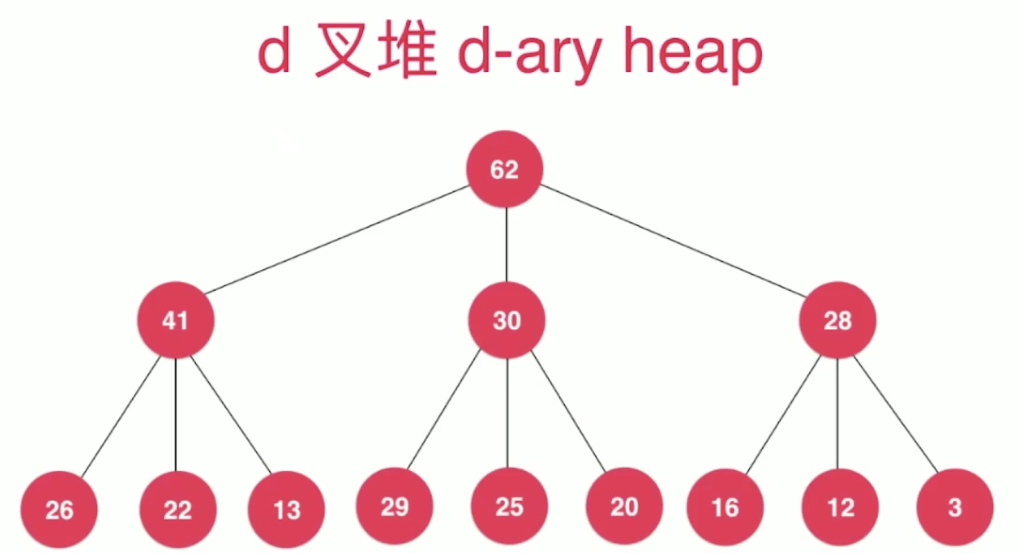
索引堆:每个元素都有一个索引,可以根据索引访问元素
广义队列:只要支持入队和出队的数据结构,就是队列
- 普通队列,优先队列
- 栈也可以理解成一个队列


