6.集合和映射
《玩转数据结构》-liuyubobobo 课程笔记
我们之前学习了二分搜索树,现在我们来学习两种高层的数据结构:集合和映射
什么叫高层数据结构呢?
就是一种定义好数据结构之后,放入应用中就能直接使用。但是其底层实现,可以是多种多样的数据结构,比如我们之前学习的栈和队列。既可以是动态数组,又可以是链表。
集合(set)
存载元素的容器,每个元素只能存在一次
我们在应用中需要这个数据结构,需要其特性来非常快速地完成去重(去除重复的元素)工作
其典型应用:客户统计,词汇量统计,访问IP统计
这里回忆一下我们上一节中学习的二分搜索树,我们在实现添加操作的时候,规定不能存放重复的元素,所以二分搜索树本身就是一个非常好的实现集合的底层数据结构。
实现
那么集合需要有哪些操作呢?
Set<E>
- void add(E) //不能添加重复元素
- void remove(E)
- boolean contains(E)
- int getSize()
- boolean isEmpty()
二分搜索树实现
这些操作我们的二分搜索树都是支持的,我们只需要将我们的二分搜索树包装一下即可
我们首先创建一个Set接口,定义集合有哪些操作
/**
* 集合
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/22
*/
public interface Set<E> {
/**
* 添加元素
* 不能添加重复的元素
* @param e 元素
*/
void add(E e);
/**
* 删除元素
* @param e 元素
*/
void remove(E e);
/**
* 判断是否包含元素
* @param e 元素
* @return boolean
*/
boolean contains(E e);
/**
* 获取集合中的元素个数
* @return int
*/
int getSize();
/**
* 判断集合是否为空
* @return boolean
*/
boolean isEmpty();
}
然后我们创建一个类,实现Set接口
import com.cupricnitrate.datastructure.tree.BinarySearchTree;
/**
* 基于二分搜索树实现的集合
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/22
*/
public class BinarySearchTreeSet<E extends Comparable<E>> implements Set<E>{
/**
* 二分搜索树
*/
private BinarySearchTree<E> tree;
public BinarySearchTreeSet(){
this.tree = new BinarySearchTree<>();
}
/**
* 添加元素
* @param e 元素
*/
@Override
public void add(E e) {
//我们在实现二分搜索树添加操作时,本身就不支持添加重复的元素
//直接使用二分搜索树的添加操作即可
tree.add(e);
}
/**
* 删除元素e
* @param e 元素
*/
@Override
public void remove(E e) {
tree.remove(e);
}
/**
* 是否包含元素e
* @param e 元素
* @return boolean
*/
@Override
public boolean contains(E e) {
return tree.contains(e);
}
/**
* 获取元素个数
* @return int
*/
@Override
public int getSize() {
return tree.size();
}
/**
* 判断集合是否为空
* @return boolean
*/
@Override
public boolean isEmpty() {
return tree.isEmpty();
}
}
这里可以看到,我们在实现类中其实什么都没有做,因为二分搜索树本身就支持了集合的所有操作。
测试
我们基于之前实现的集合类,进行以下测试
public static void main(String[] args) {
//guava创建集合的方法
List<String > list = Lists.newArrayList("a","b","c","d","a","b");
BinarySearchTreeSet<String> set = new BinarySearchTreeSet<>();
list.forEach(set::add);
System.out.println("List size: " + list.size());
System.out.println("Set size: " + set.getSize());
System.out.println("Contains word 'a'? " + set.contains("a"));
System.out.println("Contains word 'e'? " + set.contains("e"));
}
>>
List size: 6
Set size: 4
Contains word 'a'? true
Contains word 'e'? false
链表实现
我们使用二分搜索树实现了集合,那么为什么还需要用链表来实现呢?
因为链表和二分搜索树一样,都是动态数据结构
其数据都是存储在Node中的

为了能够体会到二分搜索树的性能优势所在,我们使用链表对集合进行实现,然后再比较一下两者的性能差距
import com.cupricnitrate.datastructure.linkedlist.LinkedList;
/**
* 链表实现集合
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/23
*/
public class LinkedListSet<E> implements Set<E>{
private LinkedList<E> linkedList;
public LinkedListSet(){
linkedList = new LinkedList<>();
}
/**
* 向集合中添加元素
* 不能插入相同的元素
* @param e 元素
*/
@Override
public void add(E e) {
//不能添加相同的元素
if(!linkedList.contains(e)){
//向链表头添加元素,时间复杂度为O(1)
linkedList.addFirst(e);
}
}
/**
* 删除元素e
* @param e 元素
*/
@Override
public void remove(E e) {
linkedList.removeElement(e);
}
/**
* 判断集合中是否存在元素e
* @param e 元素
* @return boolean
*/
@Override
public boolean contains(E e) {
return linkedList.contains(e);
}
/**
* 获取集合中元素的个数
* @return int
*/
@Override
public int getSize() {
return linkedList.getSize();
}
/**
* 判断集合是否为空
* @return boolean
*/
@Override
public boolean isEmpty() {
return linkedList.isEmpty();
}
}
可以看到,整体上来说,和使用二分搜索树实现集合是差不多的,只是在添加元素的时候,对是否包含相同元素进行了判断。
测试
public static void main(String[] args) {
//guava创建集合的方法
List<String > list = Lists.newArrayList("a","b","c","d","a","b");
Set<String> set = new LinkedListSet<>();
list.forEach(set::add);
System.out.println("List size: " + list.size());
System.out.println("Set size: " + set.getSize());
System.out.println("Contains word 'a'? " + set.contains("a"));
System.out.println("Contains word 'e'? " + set.contains("e"));
}
>>
List size: 6
Set size: 4
Contains word 'a'? true
Contains word 'e'? false
通过测试,可以看到链表实现的集合和二分搜索树实现的集合达成的效果是一样的
但是两者的性能上面却相差很大,我们来分析一下
集合类的复杂度分析
比较
我们先来对二分搜索树实现的集合类和链表实现的集合类进行一个比较
比较方法和上几章中比较其他几个高层数据结构的方法是一样的
import java.util.Random;
/**
* 比较集合类
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/23
*/
public class Main {
/**
* 生成随机数
* 每次生成的len位数都不相同
*
* @param param
* @return 定长的数字
*/
public static int getNotSimple(int[] param, int len) {
Random rand = new Random();
for (int i = param.length; i > 1; i--) {
int index = rand.nextInt(i);
int tmp = param[index];
param[index] = param[i - 1];
param[i - 1] = tmp;
}
int result = 0;
for (int i = 0; i < len; i++) {
result = result * 10 + param[i];
}
return result;
}
/**
* 测试集合类的时间复杂度
* @param set 集合
* @param opCount 操作数
* @return long 单位 ms
*/
private static long testSet(Set<Integer> set,int opCount){
long startTime = System.currentTimeMillis();
int[] in = { 1, 2, 3, 4, 5, 6, 7, 8 , 9 };
for(int i = 0; i < opCount; i++ ){
int rs = getNotSimple(in,5);
set.add(rs);
}
long endTime = System.currentTimeMillis();
return endTime - startTime;
}
public static void main(String[] args) {
//操作次数1w
int opCount = 10000;
Set<Integer> binarySearchTreeSet = new BinarySearchTreeSet<>();
Set<Integer> linkedListSet = new LinkedListSet<>();
System.out.println("BinarySearchTreeSet:" + testSet(binarySearchTreeSet,opCount) + "ms");
System.out.println("LinkedListSet:" + testSet(linkedListSet,opCount) + "ms");
}
}
因为我们的二分搜索树的添加采用的是递归算法,如果无脑地进行for循环插入一个递增的变量i,会导致如果变量i过大,递归方法递归太多次,虚拟机栈请求了太多的栈帧,而导致超过了虚拟机栈的栈深度,抛出stackoverflow异常。
所以我们这里采用生产随机数的方式,生成[0,10000]的数字插入,执行1w次
为了排除其随机性带来的影响,我们这里运行3次,结果如下
BinarySearchTreeSet:39ms
LinkedListSet:377ms
BinarySearchTreeSet:35ms
LinkedListSet:224ms
BinarySearchTreeSet:28ms
LinkedListSet:274ms
可以看到,链表实现的集合与二分搜索树实现的集合在时间复杂度上面相差了一个数量级
如果我们执行10w次操作,然后生成[0,100000]的随机数进行插入呢?
BinarySearchTreeSet:186ms
LinkedListSet:37971ms
这里可以看到相差的就更大了。
同理,这里只是比较粗的比较,这里的比较主要想说明二分搜索树实现的集合,在时间复杂度上面,是优于链表实现的集合的。
分析
LinkedListSet
-
增加
add()O(n)增加方法为了保证不添加重复的元素,执行了
contains()方法,去判断是否有相同的元素,contains()方法需要去遍历一次链表,所以是O(n)的时间复杂度。其链表的在头部增加的操作addFirst()的时间复杂度为O(1),所以总的来说集合的添加操作为O(n) -
查
contains()O(n)contains()方法需要去遍历链表,所以是O(n)的时间复杂度。 -
删
remove()O(n)链表的删除需要找到待删除节点的前面的那个节点,也是需要遍历链表,考虑平均时间复杂度,所以是O(n/2)=O(n)的时间复杂度
BinarySearchTreeSet
- 增加
add()O(log n) - 查
contains()O(log n) - 删
remove()O(log n)
因为二分搜索树的特性,在遍历的时候,会判断每一层的节点,去遍历其左子树和右子树,不会遍历所有的节点,每一次都会忽略一半的节点。
在添加,遍历和删除的时候,其实就是再走一个链表,从树的根节点出发,一层一层地走向树的叶子节点,最多只会经历h个节点(h为树的深度),所以对于我们的二分搜索树来说,这三个操作的时间复杂度就是O(h)
那么h和n的关系又是什么呢?
对于一个满二分搜索树,其树深度h和节点个数n的关系就为

所以对于二分搜索树实现的集合来说,增加,查询,删除的时间复杂度就为O(log n)
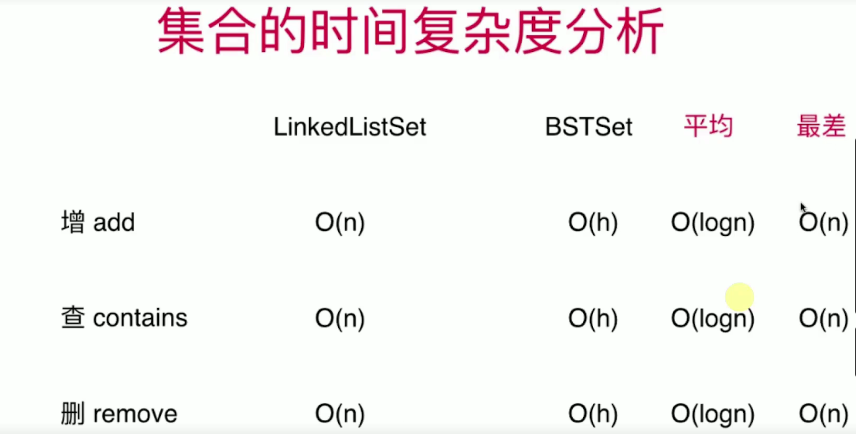
log n 是什么概念呢?我们比较一下log n 和 n

随着n越大,log n 与 n 的差距会越来越大,当n为100w时,两个时间复杂度相差了5w倍。
什么概念?
当n为100w的时候,如果一个时间复杂度为O(log n)的算法要花1s跑完,那么相对的,一个时间复杂度为O(n)的算法需要跑14h
可见O(log n )是很快的。
当然,二分搜索树实现的集合的最差情况,就为顺序插入的时候,这种情况下和链表实现的集合插入是相同的,因为总是会向右子树进行插入,所以需要先遍历全部节点再插入,此时的时间复杂度就为O(n),这也是二分搜索树的局限性。
解决这种局限性的方式就是平衡二叉树(先留个影响,后面我们再学习)
集合在的leetcode上的问题
804. 唯一摩尔斯密码词
国际摩尔斯密码定义一种标准编码方式,将每个字母对应于一个由一系列点和短线组成的字符串, 比如: a 对应 .-, b 对应 -..., c 对应 -.-., 等等。
为了方便,所有26个英文字母对应摩尔斯密码表如下:
[".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]
给定一个单词列表,每个单词可以写成每个字母对应摩尔斯密码的组合。例如,"cab" 可以写成 "-.-..--...",(即 "-.-." + ".-" + "-..." 字符串的结合)。我们将这样一个连接过程称作单词翻译。
返回我们可以获得所有词不同单词翻译的数量。
例如:
输入: words = ["gin", "zen", "gig", "msg"]
输出: 2
解释:
各单词翻译如下:
"gin" -> "--...-."
"zen" -> "--...-."
"gig" -> "--...--."
"msg" -> "--...--."
共有 2 种不同翻译, "--...-." 和 "--...--."
注意:
单词列表words 的长度不会超过 100。
每个单词 words[i]的长度范围为 [1, 12]。
每个单词 words[i]只包含小写字母。
解题模板:
class Solution {
public int uniqueMorseRepresentations(String[] words) {
}
}
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-morse-code-words
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
其实思路很简单,我们根据摩斯码,逐个计算单词中的字母,计算完成后,就把它们扔进一个集合中就好了,如果我们在扔进集合的时候,两个单词的摩斯码是相同的,则集合不会添加,因为集合不会存在相同的元素。最终我们只需要看集合中有几个元素,就是有几种不同的摩斯码。
class Solution {
public int uniqueMorseRepresentations(String[] words) {
String [] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
//使用java.util包中的集合
//其底层为红黑树实现的平衡二叉树,不会出现最差情况,即时间复杂度都为O(log n)
Set<String> set = new TreeSet<>();
for (String word : words) {
StringBuilder res = new StringBuilder();
for (int i = 0; i < word.length(); i++) {
//逐个字母获取摩斯码
res.append(codes[word.charAt(i) - 'a']);
}
set.add(res.toString());
}
return set.size();
}
}
可以看到我们有了集合这个数据结构,这个问题就非常简单
其他集合话题
有序集合和无序集合
- 有序结合中的元素具有顺序性:基于搜索树的实现,比如我们用二分搜索树实现的集合
- 无序集合中的元素没有顺序性:比如我们使用链表实现的集合,但是大多数无序集合都是基于哈希表实现的,其效率非常快,比搜索树实现的集合还要快。
很多情况下,我们不需要集合有顺序性,就可以使用性能更高的无序集合
多重集合
大多数情况下,我们不希望集合有重复的元素的,但是在某些情况下,我们也需要集合去容纳重复的元素。
其实现其实也很简单,就是基于上一章我们最后提到的支持重复元素的二分搜索树封装一层就可以了。
映射(Map)
一提到映射,很多同学就想到了高中数学中,我们学习的函数。我们在高中数学中说,一个函数就是映射
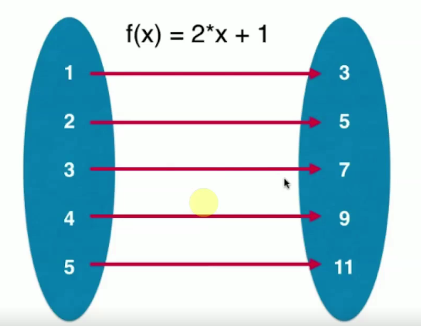
其中的意义就在于一对一的关系,即从一个值对另外一个值的对应关系。
映射这个词很抽象,为了帮助我们理解,可以将这种映射关系称之为字典(dict)
在字典中,每一个单词都有一个释意,这种从单词到释意的关系的集合,就叫做字典
在Java语言中,我们将字典这种数据结构称之为映射
存储这种键(key),值(value)数据对的数据结构,我们就称之为映射
对于这种数据结构,我们可以根据键(Key),快速地寻找到值(Value),键充当了索引的作用。
实现
映射也可以通过链表和二分搜索树去实现,原理和实现集合差不多,但是在存储节点上面需要进行一些修改

我们在节点中存储两个数据,一个是key,一个是value。
映射需要哪些操作呢?
Map<K,V>
- void add(K,V)
- V remove(K)
- boolean contains(K)
- V get(K)
- void set(K,V)
- int getSize()
- boolean isEmpty()
/**
* 映射接口
* @author 肖晟鹏
* @date 2021/4/23
*/
public interface Map<K,V> {
/**
* 增加
* @param key 键
* @param value 值
*/
void add(K key,V value);
/**
* 根据键,删除元素
* @param key 键
* @return 值 value
*/
V remove(K key);
/**
* 判断是否包含键为key的元素
* @param key 键
* @return boolean
*/
boolean contains(K key);
/**
* 根据键返回元素
* @param key 键
* @return 值 value
*/
V get(K key);
/**
* 修改键为key的值value
* @param key 键
* @param value 值
*/
void set(K key,V value);
/**
* 获取映射中的元素个数
*/
int getSize();
/**
* 判断映射是否为空
* @return boolean
*/
boolean isEmpty();
}
基于链表的实现
因为我们在映射中存储的数据是K-V键值对的,之前我们实现的链表只能存储一种数据,所以我们需要重新去实现链表
/**
* 链表实现映射
* @author 硝酸铜
* @date 2021/5/12
*/
public class LinkedListMap<K,V> implements Map<K,V>{
/**
* 节点
* 用户不需要知道节点类,用户只需要使用链表类就行了,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node{
public K key;
public V value;
public Node next;
public Node(K key,V value,Node next){
this.key = key;
this.value = value;
this.next = next;
}
public Node(K key){
this(key,null,null);
}
public Node(){
this(null,null,null);
}
@Override
public String toString() {
return key.toString() + ":" + value.toString();
}
}
/**
* 虚拟节点,链表中的真正头节点的前一个节点
* 存在意义:便于编写逻辑
* 对用户是屏蔽的,用户是不知道这个虚拟节点的存在的
*/
private Node dummyHead;
/**
* 元素个数
*/
private int size;
public LinkedListMap(){
//初始化的时候,创建虚拟节点,使其指向为空
this.dummyHead = new Node();
this.size = 0;
}
}
我们先将基础的功能写出来,在Node中,存储K-V键值对,同样的使用虚拟头结点
接下来我们去实现映射的其他功能,也就是增添改查的重头戏
import java.util.Optional;
/**
* 链表实现映射
* @author 硝酸铜
* @date 2021/5/12
*/
public class LinkedListMap<K,V> implements Map<K,V>{
/**
* 节点
* 用户不需要知道节点类,用户只需要使用链表类就行了,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node{
public K key;
public V value;
public Node next;
public Node(K key,V value,Node next){
this.key = key;
this.value = value;
this.next = next;
}
public Node(K key){
this(key,null,null);
}
public Node(){
this(null,null,null);
}
@Override
public String toString() {
return key.toString() + ":" + value.toString();
}
}
/**
* 虚拟节点,链表中的真正头节点的前一个节点
* 存在意义:便于编写逻辑
* 对用户是屏蔽的,用户是不知道这个虚拟节点的存在的
*/
private Node dummyHead;
/**
* 元素个数
*/
private int size;
public LinkedListMap(){
//初始化的时候,创建虚拟节点,使其指向为空
this.dummyHead = new Node();
this.size = 0;
}
/**
* 获取链表中的元素个数
* @return 链表中的元素个数
*/
@Override
public int getSize() {
return size;
}
/**
* 判断链表是否为空
* @return true/false
*/
@Override
public boolean isEmpty(){
return this.size == 0;
}
/**
* 通过key值,查询节点
* 用于辅助映射的增删改查
*
* @param key 键
* @return Node
*/
private Node getNode(K key){
Node cur = dummyHead.next;
while (cur != null){
if(cur.key.equals(key)){
return cur;
}
cur = cur.next;
}
return null;
}
/**
* 判断是否包含键为key的元素
* @param key 键
* @return boolean
*/
@Override
public boolean contains(K key) {
return this.getNode(key) != null;
}
/**
* 根据键返回元素
* @param key 键
* @return 值 value
*/
@Override
public V get(K key) {
/*
Node node = getNode(key);
return node == null ? null : node.value;
*/
//上面的代码同等于:
return Optional.ofNullable(this.getNode(key)).map(node -> node.value).orElse(null);
}
/**
* 增加
* @param key 键
* @param value 值
*/
@Override
public void add(K key, V value) {
//key是唯一的,所以先要进行唯一性检查
//如果不允许增加相同key下面的value:
/*if(this.contains(key)){
//可以抛异常也可以直接忽略,这里是抛异常
throw new IllegalArgumentException("Add failed.Key: " + key + " already exists!");
}*/
//如果允许,即如果key存在,则对其value进行更新
Node node = this.getNode(key);
if(node != null){
node.value = value;
}
//如果key是唯一的,就在头结点增加一个元素
dummyHead.next = new Node(key,value,dummyHead.next);
this.size++;
}
/**
* 修改键为key的值value
* @param key 键
* @param value 值
*/
@Override
public void set(K key, V value) {
Node node = this.getNode(key);
if(node == null){
throw new IllegalArgumentException("key: " + key + " doesn't exist");
}
node.value = value;
}
/**
* 根据键,删除元素
* @param key 键
* @return 值 value
*/
@Override
public V remove(K key) {
//链表删除的核心:找到待删除节点的前一个节点
//这里从dummyHead开始,防止链表为空抛出空指针异常
Node prev = dummyHead;
while (prev.next != null){
//因为是从dummyHead开始的,所以用next节点进行比较
if(prev.next.key.equals(key)){
break;
}
prev = prev.next;
}
/*
if (prev.next != null){
Node delNode = prev.next;
prev.next = delNode.next;
delNode.next = null;
}
*/
//以上代码同等于:
//lambda捕获机制:使用局部变量,lambda表达式中使用的变量应该是final或者有效的final
Node finalPrev = prev;
Optional.ofNullable(prev.next).ifPresent(node -> {
//因为prev传递到finalPrev是引用,所以操作finalPrev也能操作堆中的prev实例对象
finalPrev.next = node.next;
node.next = null;
this.size --;
});
return null;
}
}
测试
public static void main(String[] args) {
Map<String ,Integer> map = new LinkedListMap<>();
for (int i = 0; i < 10; i++) {
map.add(i+"",i);
}
System.out.println("Map size: " + map.getSize());
map.remove("5");
System.out.println("Map size: " + map.getSize());
System.out.println("Map contains key 5 : " + map.contains("5"));
System.out.println("Map get key 6 : " + map.get("6"));
}
>>
Map size: 10
Map size: 9
Map contains key 5 : false
Map get key 6 : 6
基于二分搜索树的实现
我们能够使用链表实现映射类,那么我们就能够使用二分搜索树实现映射类
回忆一下二分搜索树,我们二分搜索树存储的元素是可以比较的,所以对于二分搜索树实现的映射类来说,其key是可以比较的
并且,同样的因为我们在映射中存储的数据是K-V键值对的,之前我们实现的二分搜索树只能存储一种数据,所以我们需要重新去实现二分搜索树
我们先将映射的基本内容写出来
/**
* 二分搜索树实现映射
* @author 硝酸铜
* @date 2021/5/12
*/
public class BinarySearchTreeMap<K extends Comparable<K>,V> implements Map<K,V> {
/**
* 节点
* 用户不需要知道节点类,用户只需要使用链表类就行了,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node{
public K key;
public V value;
public Node left;
public Node right;
public Node(K key,V value){
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
@Override
public String toString() {
return key.toString() + ":" + value.toString();
}
}
/**
* 根节点
*/
private Node root;
/**
* 元素个数
*/
private int size;
@Override
public int getSize() {
return this.size;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
public BinarySearchTreeMap(){
this.root = null;
this.size = 0;
}
}
接下来我们去实现映射的增删改查
import java.util.Optional;
/**
* 二分搜索树实现映射
* @author 硝酸铜
* @date 2021/5/12
*/
public class BinarySearchTreeMap<K extends Comparable<K>,V> implements Map<K,V> {
/**
* 节点
* 用户不需要知道节点类,用户只需要使用链表类就行了,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node{
public K key;
public V value;
public Node left;
public Node right;
public Node(K key,V value){
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
@Override
public String toString() {
return key.toString() + ":" + value.toString();
}
}
/**
* 根节点
*/
private Node root;
/**
* 元素个数
*/
private int size;
@Override
public int getSize() {
return this.size;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
public BinarySearchTreeMap(){
this.root = null;
this.size = 0;
}
/**
* 增加
* @param key 键
* @param value 值
*/
@Override
public void add(K key, V value) {
this.root = this.add(this.root,key,value);
}
/**
* 向以node为根的二分搜索树中插入元素e
* 递归算法
* @param node 根
* @param key 键
* @param value 值
* @return 插入新节点后,二分搜索树的根
*/
private Node add (Node node,K key,V value){
//最基本问题
if(node == null){
this.size ++;
return new Node(key,value);
}
//递归核心问题:将其分解为更小的同样的问题,并将解组成原问题的解。
if(key.compareTo(node.key) < 0){
node.left = add(node.left,key,value);
}
else if(key.compareTo(node.key) > 0){
node.right = add(node.right,key,value);
}else {
//key.compareTo(node.key) == 0 的情况
node.value = value;
}
return node;
}
/**
* 通过key值,查询节点
* 用于辅助映射的增删改查
* 其宏观语义为:返回以Node为根节点的二分搜索树中,key所在的节点
*
* @param node 根节点
* @param key 键
* @return key所在的节点
*/
private Node getNode(Node node,K key){
//最基本的问题
if(node == null){
return null;
}
//递归核心问题:将其分解为更小的同样的问题,并将解组成原问题的解。
if(key.compareTo(node.key) == 0){
return node;
}
else if(key.compareTo(node.key) < 0){
return getNode(node.left,key);
}
else{
//key.compareTo(node.key) > 0 的情况
return getNode(node.right,key);
}
}
/**
* 判断是否包含键为key的元素
* @param key 键
* @return boolean
*/
@Override
public boolean contains(K key) {
return this.getNode(this.root,key) != null;
}
/**
* 根据键返回元素
* @param key 键
* @return 值 value
*/
@Override
public V get(K key) {
/*
Node node = getNode(this.root,key);
return node == null ? null : node.value;
*/
//上面的代码同等于:
return Optional.ofNullable(this.getNode(this.root,key))
.map(node -> node.value)
.orElse(null);
}
/**
* 修改键为key的值value
* @param key 键
* @param value 值
*/
@Override
public void set(K key, V value) {
Node node = this.getNode(this.root,key);
if(node == null){
throw new IllegalArgumentException("key: " + key + " doesn't exist");
}
node.value = value;
}
/**
* 根据键,删除元素
* @param key 键
* @return 值 value
*/
@Override
public V remove(K key) {
Node node = getNode(this.root,key);
if(node == null){
return null;
}
this.root = remove(this.root,key);
return null;
}
/**
* 删除以node 为根的二分搜索树中键为key的节点
* 递归算法
* @param node 根节点
* @param key 键
* @return
*/
private Node remove(Node node,K key){
if(node == null){
return null;
}
//元素比当前节点的元素小,遍历左子树
if(key.compareTo(node.key) < 0){
node.left = remove(node.left,key);
return node;
}
//元素比当前节点的元素大,遍历右子树
if(key.compareTo(node.key) > 0){
node.right = remove(node.right,key);
return node;
}
//元素等于当前节点的元素,进行删除操作
else {
//待删除节点左子树为空
if(node.left == null){
Node rightNode = node.right;
node.right = null;
this.size --;
return rightNode;
}
//待删除节点右子树为空
if(node.right == null){
Node leftNode = node.left;
node.left = null;
this.size --;
return leftNode;
}
//待删除节点左右子树均不为空
//逻辑:找到比待删除节点大的最小节点,即待删除节点右子树的最小节点
//用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
removeMin(node.right);
successor.right = node.right;
successor.left = node.left;
node.left = null;
node.right = null;
return successor;
}
}
/**
* 返回以node为根的二分搜索树的最小值所在的节点
* @param node 根节点
* @return
*/
private Node minimum(Node node){
if( node.left == null ) {
return node;
}
return minimum(node.left);
}
/**
* 删除掉以node为根的二分搜索树中的最小节点
* @param node 根节点
* @return 返回删除节点后新的二分搜索树的根
*/
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
}
测试
public static void main(String[] args) {
Map<String ,Integer> map = new BinarySearchTreeMap<>();
for (int i = 0; i < 10; i++) {
map.add(i+"",i);
}
System.out.println("Map size: " + map.getSize());
map.remove("5");
System.out.println("Map size: " + map.getSize());
System.out.println("Map contains key 5 : " + map.contains("5"));
System.out.println("Map get key 6 : " + map.get("6"));
}
>>
Map size: 10
Map size: 9
Map contains key 5 : false
Map get key 6 : 6
映射类的复杂度分析
比较
同样的我们先来对二分搜索树实现的映射类和链表实现的映射类进行一个比较
比较方法和上几章中比较其他几个高层数据结构的方法是一样的
import java.util.Random;
/**
* 比较映射类
* @author 硝酸铜
* @date 2021/5/12
*/
public class Main {
/**
* 生成随机数
* 每次生成的len位数都不相同
*
* @param param
* @return 定长的数字
*/
public static int getNotSimple(int[] param, int len) {
Random rand = new Random();
for (int i = param.length; i > 1; i--) {
int index = rand.nextInt(i);
int tmp = param[index];
param[index] = param[i - 1];
param[i - 1] = tmp;
}
int result = 0;
for (int i = 0; i < len; i++) {
result = result * 10 + param[i];
}
return result;
}
/**
* 测试集合类的时间复杂度
* @param map 映射
* @param opCount 操作数
* @return long 单位 ms
*/
private static long testSet(Map<String ,Integer> map,int opCount){
long startTime = System.currentTimeMillis();
int[] in = { 1, 2, 3, 4, 5, 6, 7, 8 , 9 };
for(int i = 0; i < opCount; i++ ){
int rs = getNotSimple(in,5);
map.add(rs+"",rs);
}
long endTime = System.currentTimeMillis();
return endTime - startTime;
}
public static void main(String[] args) {
//操作次数1w
int opCount = 10000;
Map<String ,Integer> binarySearchTreeMap = new BinarySearchTreeMap<>();
Map<String ,Integer> linkedListMap = new LinkedListMap<>();
System.out.println("BinarySearchTreeMap:" + testSet(binarySearchTreeMap,opCount) + "ms");
System.out.println("LinkedListMap:" + testSet(linkedListMap,opCount) + "ms");
}
}
和集合类的比较是同理的
我们运行三次,结果如下
BinarySearchTreeMap:17ms
LinkedListMap:220ms
BinarySearchTreeMap:19ms
LinkedListMap:212ms
BinarySearchTreeMap:23ms
LinkedListMap:234ms
同理,这里只是比较粗的比较,这里的比较主要想说明二分搜索树实现的集合,在时间复杂度上面,是优于链表实现的集合的。
分析
同集合

更多的映射相关话题
- 有序映射(基于搜索树)和无序映射(基于哈希表),键是否有序
- 多重映射,一键多值
- 集合和映射其实很像,我们可以根据一个已有的映射去实现集合(value为空,值考虑键)
集合类和映射类在leetcode上的问题
我们做两到leetcode上面关于映射和集合的问题,充分理解一下什么时候该用集合,什么时候该用映射
349.两个数组的交集
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
说明:
- 输出结果中的每个元素一定是唯一的。
- 我们可以不考虑输出结果的顺序。
结题模板:
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
}
}
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/intersection-of-two-arrays/submissions/
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
将第一个数组的元素放入集合中,对第二个数组进行比较,如果集合中存在,则是交集元素。因为要考虑结果中的每一个元素是唯一的,所以需要在每一次比较出交集元素之后,将其从集合中删除。
解答:
import java.util.ArrayList;
import java.util.List;
import java.util.TreeSet;
/**
* 力扣349号问题
* 给定两个数组,编写一个函数来计算它们的交集。
*
* @author 硝酸铜
* @date 2021/5/20
*/
public class SolutionB {
public int[] intersection(int[] nums1, int[] nums2) {
//树实现的集合
TreeSet<Integer> set = new TreeSet<Integer>();
for (int num : nums1){
set.add(num);
}
List<Integer> intersections = new ArrayList<>();
for (int num : nums2){
//判断交集
if(set.contains(num)){
//将结果存入交集中
intersections.add(num);
//因为要保证结果中每个元素是唯一的,所以从set中删除
set.remove(num);
}
}
//组成数组返回
int[] res = new int[intersections.size()];
for (int i = 0; i < intersections.size(); i++) {
res[i] = intersections.get(i);
}
return res;
}
}
350 两个数组的交集2
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]
说明:
- 输出结果中每个元素出现的次数,应与元素在两个数组中出现次数的最小值一致。
- 我们可以不考虑输出结果的顺序。
进阶:
- 如果给定的数组已经排好序呢?你将如何优化你的算法?
- 如果 nums1 的大小比 nums2 小很多,哪种方法更优?
- 如果 nums2 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/intersection-of-two-arrays-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题模板:
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
}
}
思路:
我们需要返回的结果中,元素的出现的次数是元素在两个数组中出现次数的最小值,这一点我们可以通过记录元素在数组总出现的频次来实现。因为要记录元素出现的频次,则我们用映射来记录元素出现的频次
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.TreeMap;
/**
* 力扣350号问题
* @author 硝酸铜
* @date 2021/5/20
*/
public class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
//<元素,频次>
Map<Integer,Integer> map = new TreeMap<>();
//记录集合1中的元素与其出现的频次
for (int num : nums1){
if(!map.containsKey(num)){
map.put(num,1);
}else {
map.put(num,map.get(num) + 1);
}
}
//记录交集,因为记录了频次,所以保证了结果中元素的频次为两数组中元素的频次的最小值
List<Integer> list = new ArrayList<>();
for (int num:nums2) {
if (map.containsKey(num)) {
list.add(num);
//频次减1
map.put(num, map.get(num) - 1);
//频次为0的时候,删除元素
if (map.get(num) == 0) {
map.remove(num);
}
}
}
//组成数组返回
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++) {
res[i] = list.get(i);
}
return res;
}
}
上面两个问题,我们使用了不同的数据结构来解决问题


