5.二分搜索树
《玩转数据结构》-liuyubobobo 课程笔记
树结构
线性结构:将元素排成一排进行存储
树形结构:从根出发,长出枝杈,长出的枝杈中,还会有更多的枝杈,直到最后的树叶。
为什么会有树结构呢?
-
树结构本身是一种天然地组织结构:树结构其实并不抽象,我们生活中经常会使用到树结构,比如电脑中的文件夹,部门的分级,图书的分类,家谱等等。
-
高效:将数据使用树结构存储之后,出奇的高效。
二叉树
在学习二分查找树之前,我们先来看一下什么叫做二叉树
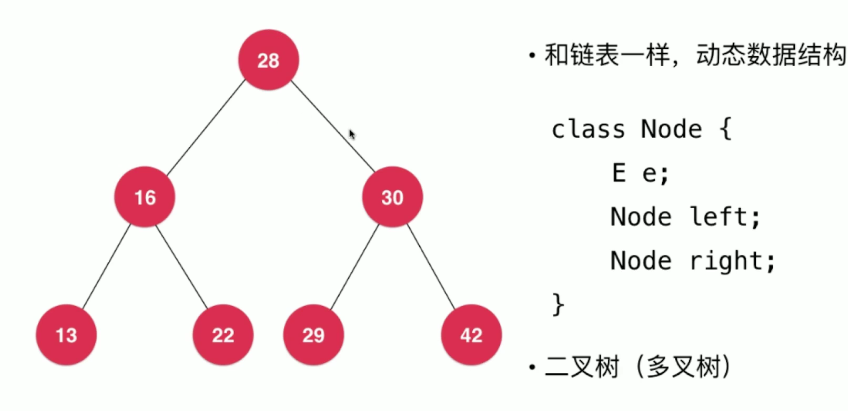
对于二叉树来说,每个节点都最多分为两个树杈
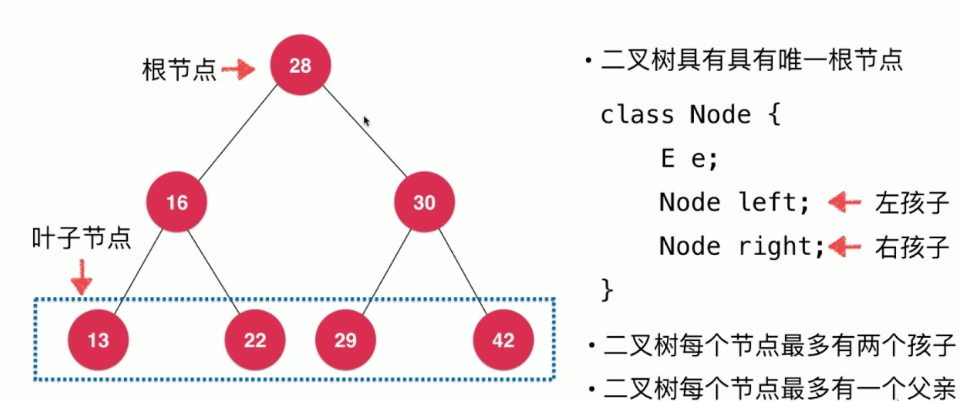
叶子节点不一定在最底层,因为二叉树不一定都是上图这么工整的。叶子节点的定义是左右孩子都为空
二叉树具有天然递归结构:每一个节点的左/右子树也是二叉树
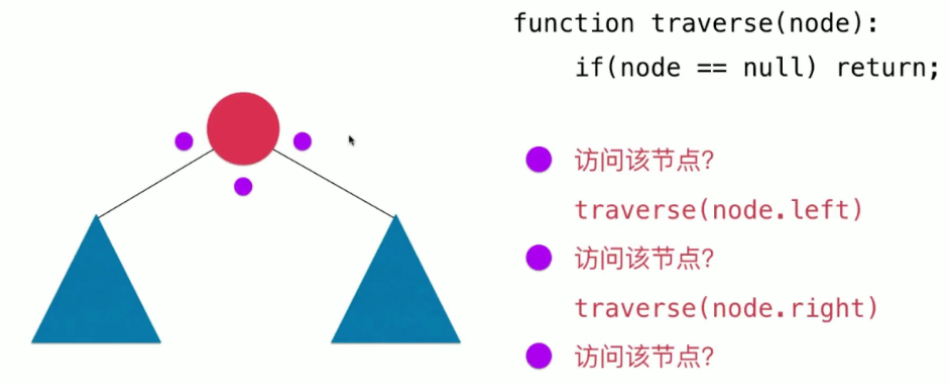
和线性结构不同,树形结构使用递归来遍历更为简单。
当然,二叉树不一定是满的,下面这个树也是二叉树
一个节点,或者为空,都是二叉树
二分搜索树
定义
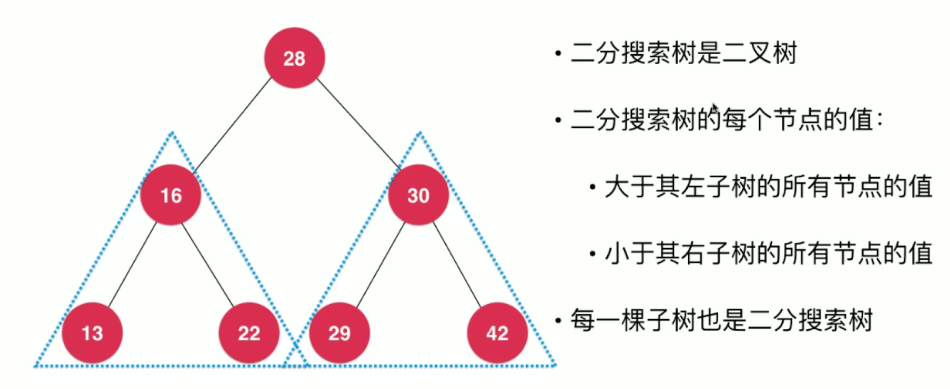
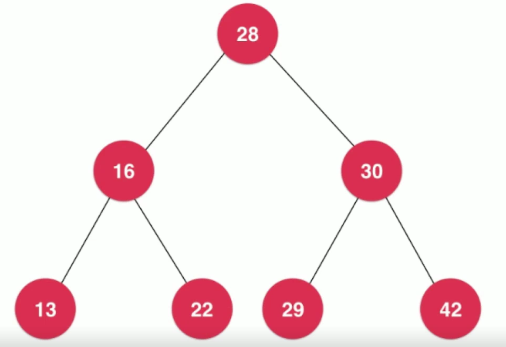
28大于左子树中的所有节点的值,小于右子树中所有节点的值
利用这一个特性,如果我们需要在二分搜索树中查询某一个值,那么我们只需要对每一层的节点进行判断,然后选择一边的子树进行遍历即可,大大的加快了查询速度。比如查找42,因为42 > 28则直接从28节点的右子树进行遍历,左子树就不需要去遍历了。同理42 > 30,则从节点30的右子树去遍历查找。
因为有这种特性,所以要求二分搜索树中存储的元素必须有可比较性
实现
首先我们编写二叉搜索树的基本代码
/**
* 二分搜索树
* 存储的元素必须有可比较性,所以泛型的类型必须实现Comparable接口
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/16
*/
public class BinarySearchTree<E extends Comparable<E>> {
/**
* 节点
* 用户不需要知道节点类,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node {
public E e;
public Node left;
public Node right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
/**
* 根节点
*/
private Node root;
/**
* 元素个数
*/
private int size;
public BinarySearchTree(){
this.root = null;
this.size = 0;
}
/**
* 获取元素个数
* @return 元素个数
*/
public int size(){
return this.size;
}
/**
* 判断树是否为空
* @return true/false
*/
public boolean isEmpty(){
return this.size == 0;
}
}
添加元素
之前说过,使用递归来实现树的遍历比起循环来说,要简单得多,我们这里就使用递归来实现添加元素的操作。
回忆之前学习的递归:
所有递归算法都可以分为两部分的:
- 求解最基本的问题:最基本的问题是不能分解的,需要我们自己编写逻辑
- 递归算法最核心的部分--把原问题转化为更小的问题:我们需要将更小的问题的答案,构建出原问题的答案。
我们这里最基本的问题是什么?
当元素不断地在二叉搜索树中进行比较移动,最后来到叶子节点的时候,判断其是叶子节点的左孩子还是右孩子。
怎么将原问题转化为更小的问题?
将元素插入左子树或者右子树
/**
* 向二分搜索树中插入元素e
* @param e 待插入元素
*/
public void add(E e){
//当二叉树为空的时候
if(this.root == null){
this.root = new Node(e);
this.size ++ ;
}
else {
add(this.root,e);
}
}
/**
* 向以node为根的二分搜索树中插入元素e
* 递归算法
* @param node 根
* @param e 待插入元素
*/
private void add (Node node,E e){
//如果相等,则不进行插入
if(e.equals(node.e)){
return;
}
//最基本问题
//如果待插入元素小于node存储的元素,并且node的左子树为空
else if(e.compareTo(node.e) < 0 && node.left == null){
//直接作为左孩子即可
node.left = new Node(e);
this.size ++;
return;
}
else if(e.compareTo(node.e) > 0 && node.right == null){
//直接作为右孩子即可
node.right = new Node(e);
this.size ++;
return;
}
//递归核心问题:将其分解为更小的同样的问题,并将解组成原问题的解。
if(e.compareTo(node.e) < 0){
add(node.left,e);
}else {
add(node.right,e);
}
}
注意这里的宏观语义:向以node为根的二叉搜索树中插入元素e
当然,这里的实现方式还是有瑕疵的:
- 我们对树的根节点进行了一次判断,判断其根节点是否为空(即判断树是否为空)。这一步和之后的操作不统一。
- 在进行插入的时候,我们进行了两次比较,第一次比较是否是叶子节点,如果不是,则会进行第二次比较,是插入左子树还是右子树。
- 递归的终止条件太过于臃肿。函数的宏观语义是:向以
node为根的二分搜索树中插入元素e。之前我们说过,null也是二分搜索树,node是可以为空的,当node为空的时候,则必须创建一个节点。以这样的思想,我们可以对终止条件进行修改(修改解决最基本问题的逻辑)
根据这几点,我们进行优化
/**
* 向二分搜索树中插入元素e
* @param e 待插入元素
*/
public void add(E e){
this.root = add(this.root,e);
}
/**
* 向以node为根的二分搜索树中插入元素e
* 递归算法
* @param node 根
* @param e 待插入元素
* @return 插入新节点后,二分搜索树的根
*/
private Node add (Node node,E e){
//最基本问题
if(node == null){
this.size ++;
return new Node(e);
}
//递归核心问题:将其分解为更小的同样的问题,并将解组成原问题的解。
if(e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if(e.compareTo(node.e) > 0){
node.right = add(node.right,e);
}
return node;
}
查询元素
在理解怎么添加元素之后,对于怎么实现查询元素的操作就很简单了。只需要在遍历的时候进行判断即可。
/**
* 判断二分搜索树中是否包含元素e
* @param e
* @return boolean
*/
public boolean contains(E e){
return contains(this.root,e);
}
/**
* 判断以Node为根的二分搜索树中是否包含元素e
* @param node 根节点
* @param e 元素
* @return boolean
*/
private boolean contains(Node node,E e){
//最基本问题
//根节点为空直接返回false
if(node == null){
return false;
}
//相等则说明包含,返回true
if(e.compareTo(node.e) == 0 ){
return true;
}
//核心问题
else if(e.compareTo(node.e) < 0){
return contains(node.left,e);
}
else {
return contains(node.right,e);
}
}
和java1.8特性结合,等同于这个函数
Optional<Node> op = Optional.ofNullable(node);
return op.filter(n -> {
//最基本问题
//相等则说明包含,返回true
if(e.compareTo(n.e) == 0 ){
return true;
}
//核心问题
else if(e.compareTo(n.e) < 0){
return contains(n.left,e);
}
else {
return contains(n.right,e);
}
}).isPresent();
遍历
二分搜索树的遍历分为两个大类:
- 深度优先遍历
- 广度优先遍历(层序遍历)
深度优先遍历
我们先看看深度优先遍历
深度优先遍历又分为三种:先序遍历,中序遍历和后序遍历
- 前序遍历:先访问当前节点,再依次递归访问左右子树。
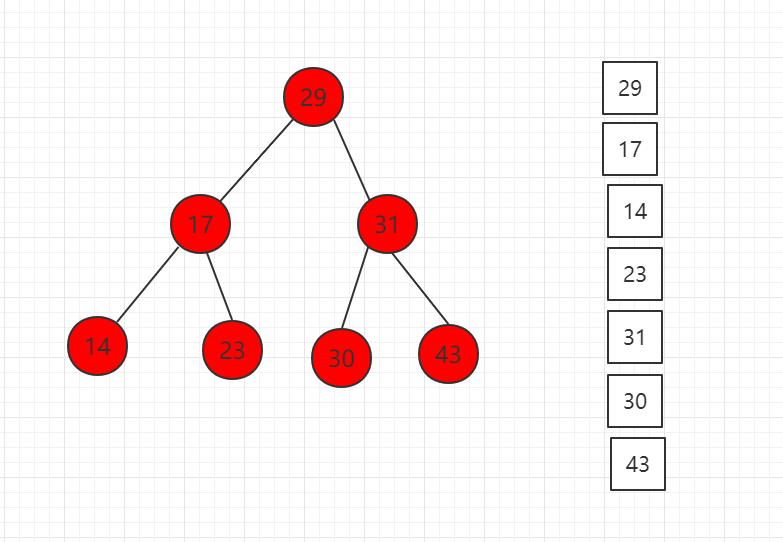
- 中序遍历:先递归访问左子树,再访问自身,再递归访问右子树。
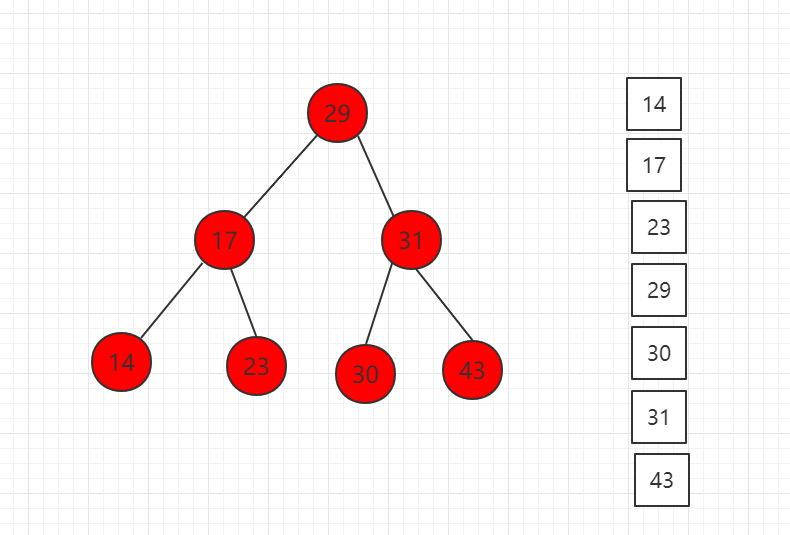
- 后序遍历:先递归访问左右子树,再访问自身节点。
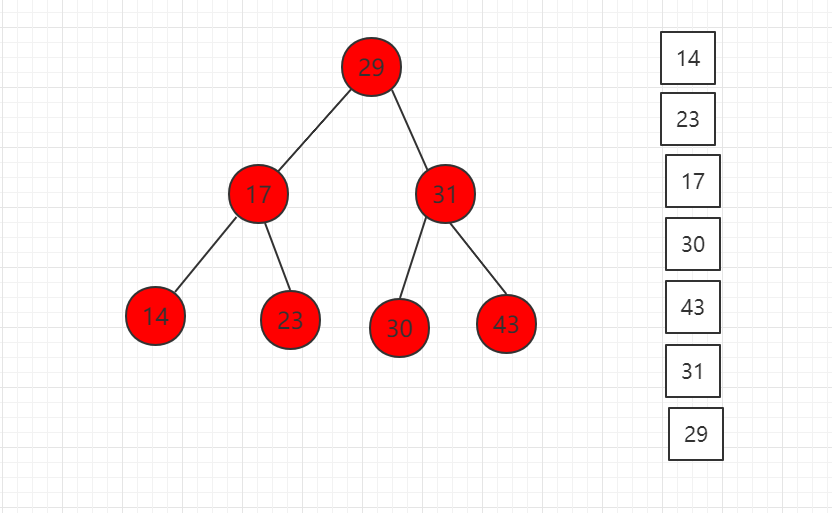
这三个遍历的不同在于访问当前节点的顺序不同,导致他们使用的场景也不同
- 前序遍历:是最自然的遍历方式,也是我们最常用的遍历方式。用于需要先处理当前节点的问题之后再访问孩子节点的场景。
- 中序遍历:会导致二分搜索树的自然排序,其原因是其遍历的顺序:先遍历比当前节点小的节点,再访问当前节点,之后再去遍历比当前节点大的节点。最后得到的结果自然是顺序的结果。这也是二分搜索树额外的效能,也是其被称之为排序树的原因。
- 后序遍历:先处理左子树和右子树,在处理当前节点。经常用于释放内存,先释放左子树和右子树的内存,再释放当前节点的内存。
/**
* 深度优先遍历
* @param i 1为先序遍历,0为中序遍历,-1为广度优先遍历
*/
public void order(int i){
switch (i){
case 1:
//先序遍历
preOrder(this.root);
break;
case 0:
//中序遍历
inOrder(this.root);
break;
case -1:
//后序遍历
postOrder(this.root);
break;
default:
break;
}
}
/**
* 以node为根节点,进行前序遍历
* @param node 根节点
*/
private void preOrder(Node node){
if(node == null){
return;
}
//先处理本身
System.out.println(node.e);
//再遍历左子树
preOrder(node.left);
//最后遍历右子树
preOrder(node.right);
}
/**
* 以node为根节点,进行后序遍历
* @param node 根节点
*/
private void postOrder(Node node){
if(node == null){
return;
}
//先遍历左子树
postOrder(node.left);
//再遍历右子树
postOrder(node.right);
//再处理本身
System.out.println(node.e);
}
/**
* 以node为根节点,进行中序遍历
* @param node 根节点
*/
private void inOrder(Node node){
if(node == null){
return;
}
//先遍历左子树
inOrder(node.left);
//再处理本身
System.out.println(node.e);
//最后遍历右子树
inOrder(node.right);
}
前序遍历的非递归写法
我们之前实现遍历时,使用的是递归写法,因为在树形结果中,使用递归更为简单。
我们这里因为是学习数据结构,需要从不同的角度去看待问题。我们这里就研究一下前序遍历的非递归写法(中序遍历和后序遍历可以用非递归的方法来实现,只是代码相对复杂并且实际应用不多,就主要研究前序遍历即可)
让我们来回忆一下前序遍历:

我们先访问当前节点,然后再访问左子树,然后再访问右子树。
这里可以回忆一下栈这个数据结构。我们在研究栈这个数据结构的时候,讲到过程序调用的系统栈,这里我们也可以使用栈来记录我们访问的路径。
当我们遍历一个根节点为node树时,先将node压入栈中,然后将其出栈,进行处理
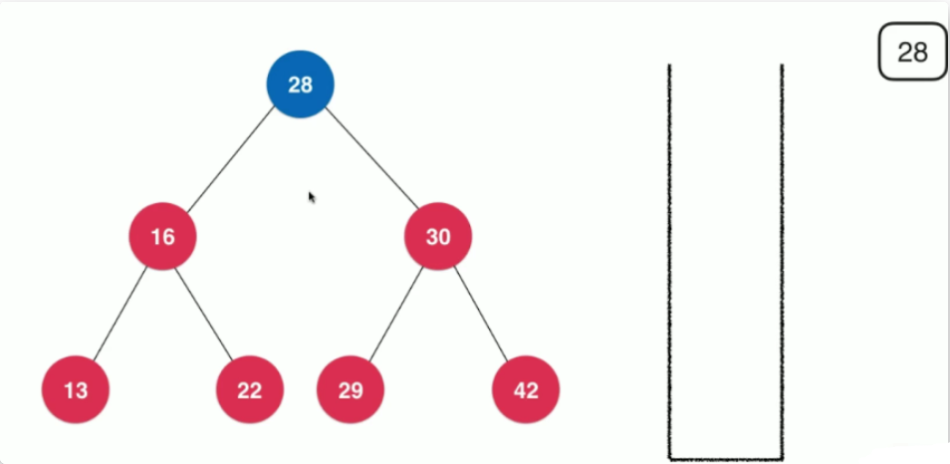
再根据访问顺序,将node.right,node.left依次压入栈中,因为其栈的后进先出的特性,依次遍历栈顶节点,即先遍历node.left之后,再遍历node.right
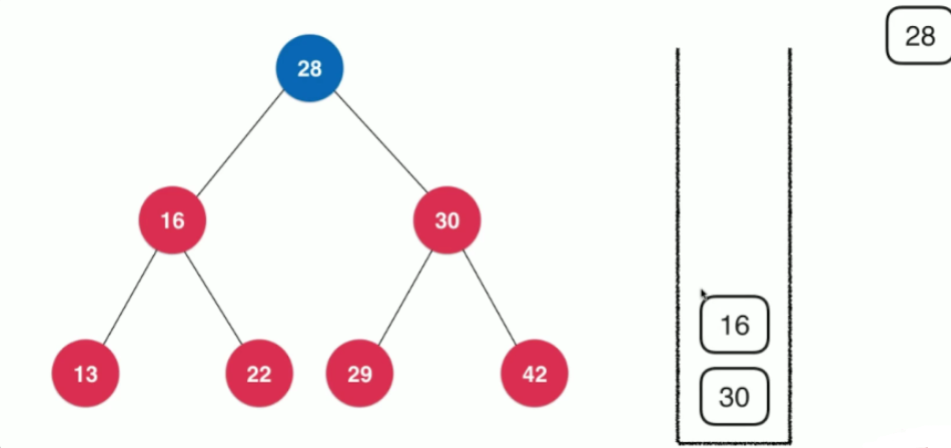
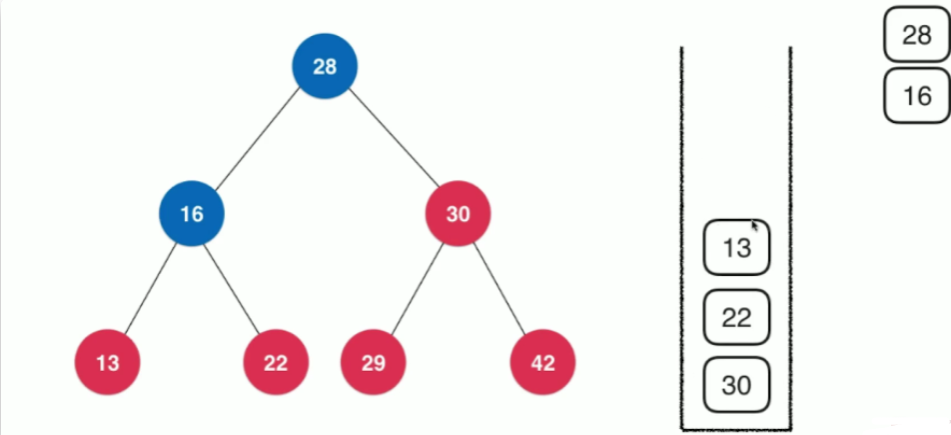
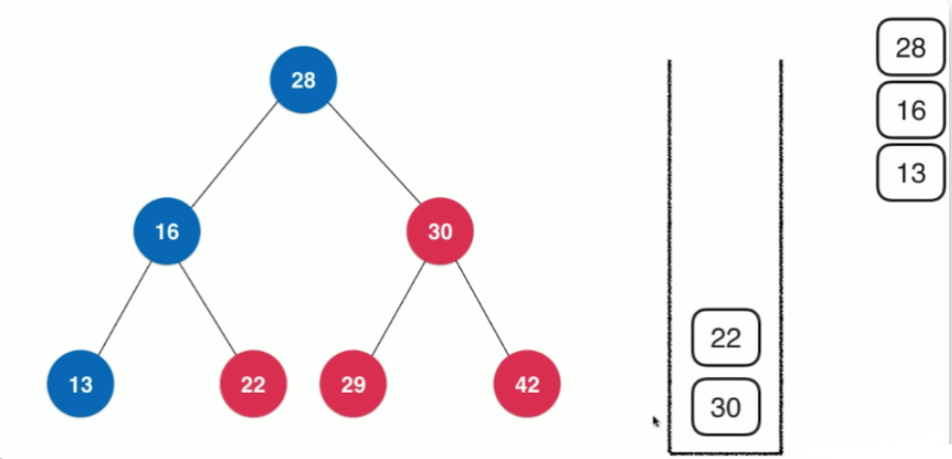
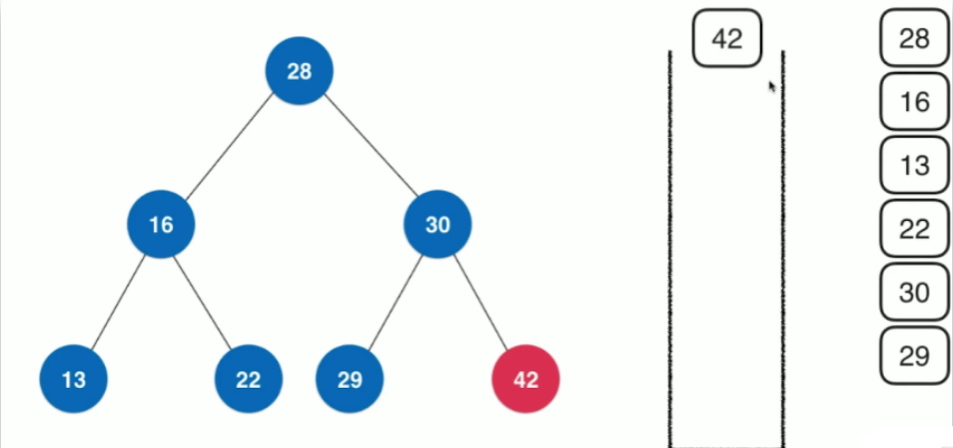
/**
* 以node为根节点,进行前序遍历
* 非递归算法
*/
private void preOrderNR(){
Stack<Node> stack = new Stack<>();
//先将根节点进行入栈
stack.push(this.root);
while (!stack.empty()){
//访问当前节点,对其继续出栈
Node cur =stack.pop();
System.out.println(cur.e);
//根据访问顺序,先将右子树压入栈,再将左子树压入栈
if(cur.right != null){
stack.push(cur.right);
}
if(cur.left != null){
stack.push(cur.left);
}
}
}
二分搜索树的非递归,比递归实现复杂很多,而且还需要依赖于其他的数据结构:栈
中序遍历和后序遍历的非递归实现更为复杂,并且应用场景不广。
广度优先遍历(层序遍历)
之前我们学习了二分搜索树的深度优先遍历,现在我们来看看广度优先遍历
广度优先遍历其实很好理解,在二分搜索树中,每一个节点都有一个深度的值,我们以索引的定义为准,设定二分搜索树的根节点的深度为0。在广度优先遍历中,先遍历第0层的节点,再遍历第1层的节点,以此类推
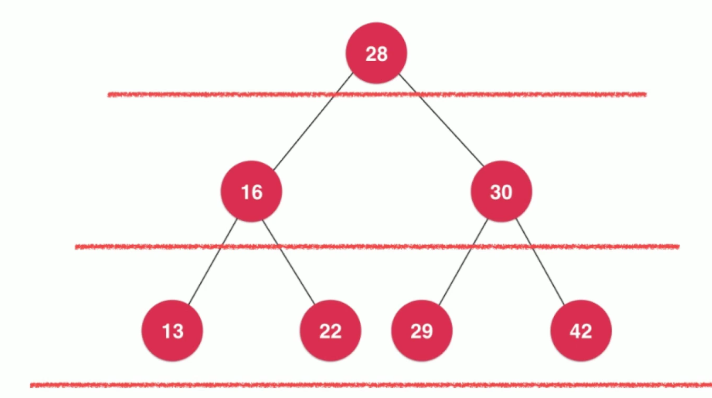
对于广度优先的实现,一般不是使用递归的方式实现的,而且需要依赖队列这个数据结构。
在每一层中,根据从左到右的顺序对节点进行入队和出队操作
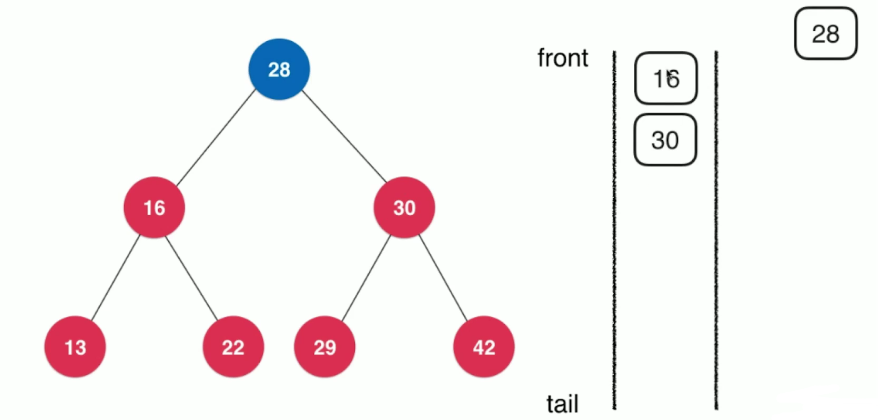
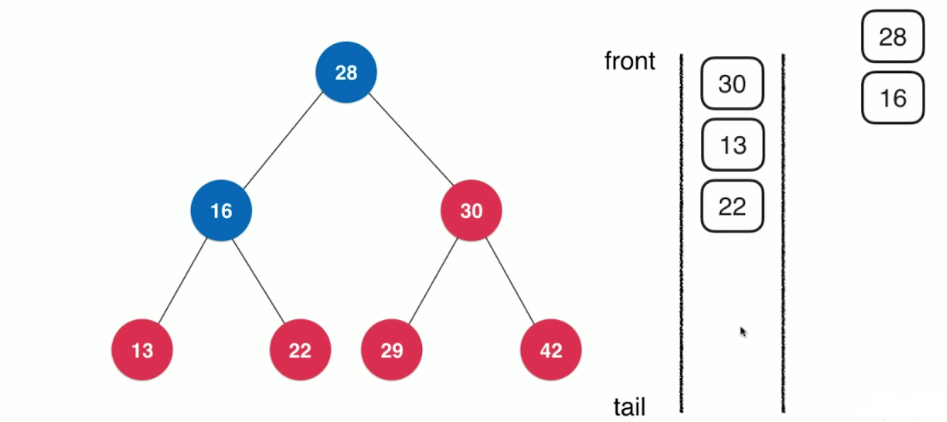
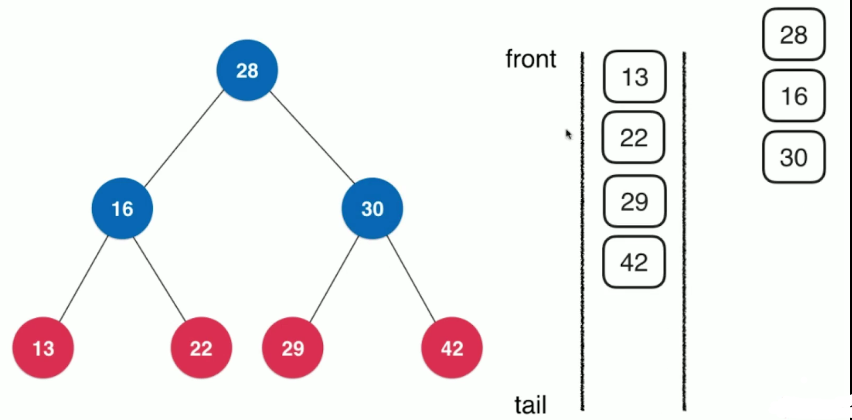
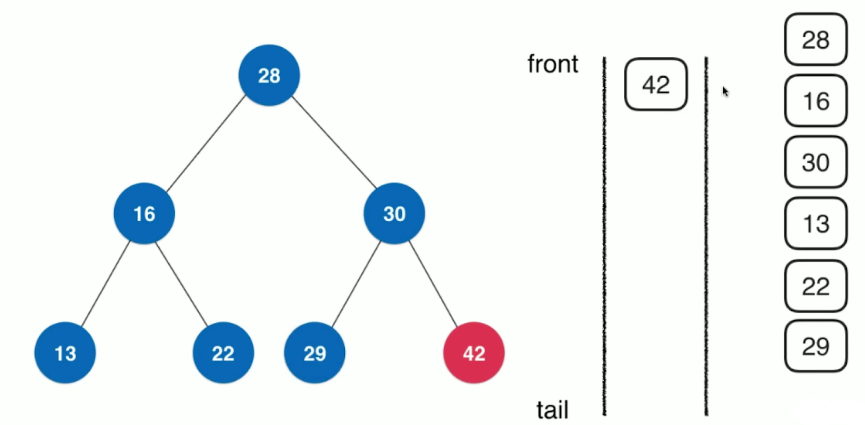
/**
* 广度优先队列
*/
public void levelOrder(){
Queue<Node> q = new LinkedList<>();
//根节点入队
q.add(this.root);
while (!q.isEmpty()){
//访问节点,出队
Node cur = q.remove();
System.out.println(cur.e);
//左孩子入队
Optional.ofNullable(cur.left).ifPresent(q::add);
//右孩子入队
Optional.ofNullable(cur.right).ifPresent(q::add);
/*同等与下面的代码
//左孩子入队
if(cur.left != null){
q.add(cur.left);
}
//右孩子入队
if(cur.right != null){
q.add(cur.right);
}*/
}
}
public static void main(String[] args) {
BinarySearchTree<Integer> tree = new BinarySearchTree<>();
tree.add(6);
tree.add(8);
tree.add(4);
tree.add(2);
tree.add(11);
tree.levelOrder();
}
>>
6
4
8
2
11
广度优先的意义:能够更快地找到想要搜索的那个元素。
其主要用于搜索的策略上。常用语算法设计中 - 最短路径
删除元素
删除最大/最小元素
为了理解删除元素这个操作,我们先从简单的删除最大/最小元素这个操作出发。
删除最大/最小元素,从二分搜索树的特性出发,就是删除最右边的节点/最左边的节点,也就是一直找节点的右孩子/左孩子,直到找到没有右孩子/左孩子的节点,那就是最大/最小的节点
其核心操作是找到最大/最小元素,找到之后,对其进行删除即可
/**
* 寻找二分搜索树的最小元素
* @return
*/
public E minimum(){
if(size == 0) {
throw new IllegalArgumentException("BST is empty");
}
Node minNode = minimum(root);
return minNode.e;
}
/**
* 返回以node为根的二分搜索树的最小值所在的节点
* @param node 根节点
* @return
*/
private Node minimum(Node node){
if( node.left == null ) {
return node;
}
return minimum(node.left);
}
/**
* 寻找二分搜索树的最大元素
* @return 最大元素
*/
public E maximum(){
if(size == 0) {
throw new IllegalArgumentException("BST is empty");
}
return maximum(root).e;
}
/**
* 返回以node为根的二分搜索树的最大值所在的节点
* @param node 根节点
* @return 最大值所在的节点
*/
private Node maximum(Node node){
if( node.right == null ) {
return node;
}
return maximum(node.right);
}
/**
* 从二分搜索树中删除最小值所在节点
* @return 返回最小值
*/
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
/**
* 删除掉以node为根的二分搜索树中的最小节点
* @param node 根节点
* @return 返回删除节点后新的二分搜索树的根
*/
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
/**
* 从二分搜索树中删除最大值所在节点
* @return 最大值
*/
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
/**
* 删除掉以node为根的二分搜索树中的最大节点
* @param node 根节点
* @return 返回删除节点后新的二分搜索树的根
*/
private Node removeMax(Node node){
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
删除左右都有孩子的节点
删除元素难点在于,如何去删除一个左右都有孩子的节点?比如删除如下二分搜索树中的58这个节点
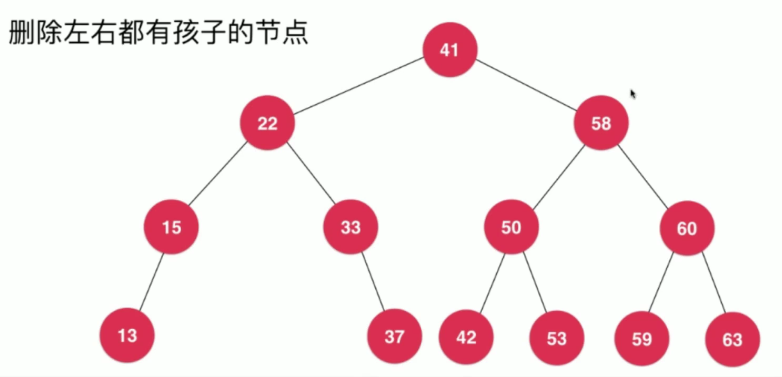
这个方法可以被称为Hibbard Deletion是Hibbard在1962年提出的方法
我们需要删除值为58的节点,这里我们将这个节点命名为d,其有左孩子和右孩子,如果我们需要对其进行删除,那么我们必须要找一个孩子节点来替代节点d,即找到d的后继
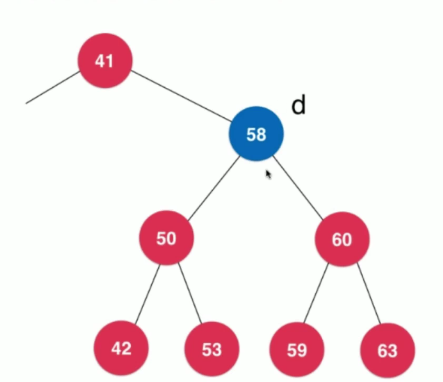
我们需要去找到比节点d的值大的,但是差距最小的节点,也就是节点值为59的节点。
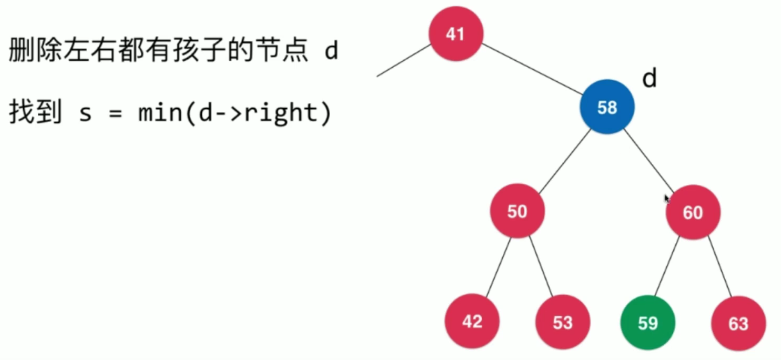
那么我们怎么找到这个节点呢?只需要找到右子树中的最小值的节点即可。因为根据二分搜索树的性质,其右子树中所有的节点的值都比节点d的值大,所以找到右子树中最小值的节点就可以了。
这个时候,值为59的节点就是节点d的后继,我们将其称为节点s
接下来我们将节点s代替节点d即可。
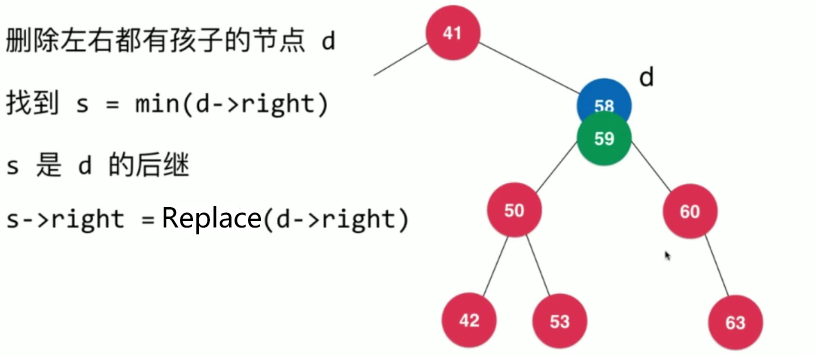
最后删除节点d
/**
* 删除以node 为根的二分搜索树中值为e的节点
* 递归算法
* @param node
* @param e
* @return
*/
private Node remove(Node node,E e){
if(node == null){
return null;
}
//元素比当前节点的元素小,遍历左子树
if(e.compareTo(node.e) < 0){
node.left = remove(node.left,e);
return node;
}
//元素比当前节点的元素大,遍历右子树
if(e.compareTo(node.e) > 0){
node.right = remove(node.right,e);
return node;
}
//元素等于当前节点的元素,进行删除操作
else {
//待删除节点左子树为空
if(node.left == null){
Node rightNode = node.right;
node.right = null;
this.size --;
return rightNode;
}
//待删除节点右子树为空
if(node.right == null){
Node leftNode = node.left;
node.left = null;
this.size --;
return leftNode;
}
//待删除节点左右子树均不为空
//逻辑:找到比待删除节点大的最小节点,即待删除节点右子树的最小节点
//用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
removeMin(node.right);
successor.right = node.right;
successor.left = node.left;
node.left = null;
node.right = null;
return successor;
}
}
我这里是寻找节点d的后继,当然也可去寻找d的前驱,即寻找节点d左子树中的最大值,也是一样的。
整体实现
import java.util.LinkedList;
import java.util.Optional;
import java.util.Queue;
import java.util.Stack;
/**
* 二分搜索树
* 存储的元素必须有可比较性,所以泛型的类型必须实现Comparable接口
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/4/16
*/
public class BinarySearchTree<E extends Comparable<E>> {
/**
* 节点
* 用户不需要知道节点类,所以节点作为内部类
* 我们需要对用户屏蔽数据结构中的实现细节
*/
private class Node {
public E e;
public Node left;
public Node right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
/**
* 根节点
*/
private Node root;
/**
* 元素个数
*/
private int size;
public BinarySearchTree(){
this.root = null;
this.size = 0;
}
/**
* 获取元素个数
* @return 元素个数
*/
public int size(){
return this.size;
}
/**
* 判断树是否为空
* @return true/false
*/
public boolean isEmpty(){
return this.size == 0;
}
/**
* 向二分搜索树中插入元素e
* @param e 待插入元素
*/
public void add(E e){
this.root = add(this.root,e);
}
/**
* 向以node为根的二分搜索树中插入元素e
* 递归算法
* @param node 根
* @param e 待插入元素
* @return 插入新节点后,二分搜索树的根
*/
private Node add (Node node,E e){
//最基本问题
if(node == null){
this.size ++;
return new Node(e);
}
//递归核心问题:将其分解为更小的同样的问题,并将解组成原问题的解。
if(e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if(e.compareTo(node.e) > 0){
node.right = add(node.right,e);
}
return node;
}
/**
* 判断二分搜索树中是否包含元素e
* @param e
* @return boolean
*/
public boolean contains(E e){
return contains(this.root,e);
}
/**
* 判断以Node为根的二分搜索树中是否包含元素e
* @param node 根节点
* @param e 元素
* @return boolean
*/
private boolean contains(Node node,E e){
Optional<Node> op = Optional.ofNullable(node);
return op.filter(n -> {
//最基本问题
//相等则说明包含,返回true
if(e.compareTo(n.e) == 0 ){
return true;
}
//核心问题
else if(e.compareTo(n.e) < 0){
return contains(n.left,e);
}
else {
return contains(n.right,e);
}
}).isPresent();
/*//最基本问题
//根节点为空直接返回false
if(node == null){
return false;
}
//相等则说明包含,返回true
if(e.compareTo(node.e) == 0 ){
return true;
}
//核心问题
else if(e.compareTo(node.e) < 0){
return contains(node.left,e);
}
else {
return contains(node.right,e);
}*/
}
/**
* 深度优先遍历
* @param i 1为先序遍历,0为中序遍历,-1为广度优先遍历
*/
public void order(int i){
switch (i){
case 1:
//先序遍历
preOrder(this.root);
break;
case 0:
//中序遍历
inOrder(this.root);
break;
case -1:
//后序遍历
postOrder(this.root);
break;
default:
break;
}
}
/**
* 以node为根节点,进行前序遍历
* @param node 根节点
*/
private void preOrder(Node node){
Optional<Node> op = Optional.ofNullable(node);
op.ifPresent(n -> {
//先处理本身
System.out.println(node.e);
//再遍历左子树
preOrder(node.left);
//最后遍历右子树
preOrder(node.right);
});
/*if(node == null){
return;
}
//先处理本身
System.out.println(node.e);
//再遍历左子树
preOrder(node.left);
//最后遍历右子树
preOrder(node.right);*/
}
/**
* 以node为根节点,进行前序遍历
* 非递归算法
*/
private void preOrderNR(){
Stack<Node> stack = new Stack<>();
//先将根节点进行入栈
stack.push(this.root);
while (!stack.empty()){
//访问当前节点,对其继续出栈
Node cur =stack.pop();
System.out.println(cur.e);
//根据访问顺序,先将右子树压入栈,再将左子树压入栈
Optional.ofNullable(cur.right).ifPresent(stack::push);
Optional.ofNullable(cur.left).ifPresent(stack::push);
/*if(cur.right != null){
stack.push(cur.right);
}
if(cur.left != null){
stack.push(cur.left);
}*/
}
}
/**
* 以node为根节点,进行后序遍历
* @param node 根节点
*/
private void postOrder(Node node){
Optional<Node> op = Optional.ofNullable(node);
op.ifPresent(n -> {
//先遍历左子树
postOrder(node.left);
//再遍历右子树
postOrder(node.right);
//再处理本身
System.out.println(node.e);
});
/*if(node == null){
return;
}
//先遍历左子树
postOrder(node.left);
//再遍历右子树
postOrder(node.right);
//再处理本身
System.out.println(node.e);*/
}
/**
* 以node为根节点,进行中序遍历
* @param node 根节点
*/
private void inOrder(Node node){
Optional<Node> op = Optional.ofNullable(node);
op.ifPresent(n -> {
//先遍历左子树
inOrder(node.left);
//再处理本身
System.out.println(node.e);
//最后遍历右子树
inOrder(node.right);
});
/*if(node == null){
return;
}
//先遍历左子树
inOrder(node.left);
//再处理本身
System.out.println(node.e);
//最后遍历右子树
inOrder(node.right);*/
}
/**
* 广度优先队列
*/
public void levelOrder(){
Queue<Node> q = new LinkedList<>();
//根节点入队
q.add(this.root);
while (!q.isEmpty()){
//访问节点,出队
Node cur = q.remove();
System.out.println(cur.e);
//左孩子入队
Optional.ofNullable(cur.left).ifPresent(q::add);
//右孩子入队
Optional.ofNullable(cur.right).ifPresent(q::add);
/*同等与下面的代码
//左孩子入队
if(cur.left != null){
q.add(cur.left);
}
//右孩子入队
if(cur.right != null){
q.add(cur.right);
}*/
}
}
/**
* 寻找二分搜索树的最小元素
* @return
*/
public E minimum(){
if(size == 0) {
throw new IllegalArgumentException("BST is empty");
}
Node minNode = minimum(root);
return minNode.e;
}
/**
* 返回以node为根的二分搜索树的最小值所在的节点
* @param node 根节点
* @return
*/
private Node minimum(Node node){
if( node.left == null ) {
return node;
}
return minimum(node.left);
}
/**
* 寻找二分搜索树的最大元素
* @return 最大元素
*/
public E maximum(){
if(size == 0) {
throw new IllegalArgumentException("BST is empty");
}
return maximum(root).e;
}
/**
* 返回以node为根的二分搜索树的最大值所在的节点
* @param node 根节点
* @return 最大值所在的节点
*/
private Node maximum(Node node){
if( node.right == null ) {
return node;
}
return maximum(node.right);
}
/**
* 从二分搜索树中删除最小值所在节点
* @return 返回最小值
*/
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
/**
* 删除掉以node为根的二分搜索树中的最小节点
* @param node 根节点
* @return 返回删除节点后新的二分搜索树的根
*/
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
/**
* 从二分搜索树中删除最大值所在节点
* @return 最大值
*/
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
/**
* 删除掉以node为根的二分搜索树中的最大节点
* @param node 根节点
* @return 返回删除节点后新的二分搜索树的根
*/
private Node removeMax(Node node){
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
/**
* 删除元素
* @param e 待删除元素
*/
public void remove(E e){
remove(this.root,e);
}
/**
* 删除以node 为根的二分搜索树中值为e的节点
* 递归算法
* @param node
* @param e
* @return
*/
private Node remove(Node node,E e){
if(node == null){
return null;
}
//元素比当前节点的元素小,遍历左子树
if(e.compareTo(node.e) < 0){
node.left = remove(node.left,e);
return node;
}
//元素比当前节点的元素大,遍历右子树
if(e.compareTo(node.e) > 0){
node.right = remove(node.right,e);
return node;
}
//元素等于当前节点的元素,进行删除操作
else {
//待删除节点左子树为空
if(node.left == null){
Node rightNode = node.right;
node.right = null;
this.size --;
return rightNode;
}
//待删除节点右子树为空
if(node.right == null){
Node leftNode = node.left;
node.left = null;
this.size --;
return leftNode;
}
//待删除节点左右子树均不为空
//逻辑:找到比待删除节点大的最小节点,即待删除节点右子树的最小节点
//用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
removeMin(node.right);
successor.right = node.right;
successor.left = node.left;
node.left = null;
node.right = null;
return successor;
}
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
generateBSTString(root, 0, res);
return res.toString();
}
/**
* 生成以node为根节点,深度为depth的描述二叉树的字符串
* @param node 根节点
* @param depth 深度
* @param res
*/
private void generateBSTString(Node node, int depth, StringBuilder res){
if(node == null){
res.append(generateDepthString(depth) + "null\n");
return;
}
res.append(generateDepthString(depth) + node.e +"\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth + 1, res);
}
/**
* ‘--’代表深度为1
* ‘----’代表深度为2
* 以‘--’ 为一个深度,以此类推。
* @param depth 深度
* @return 节点的String
*/
private String generateDepthString(int depth){
StringBuilder res = new StringBuilder();
for(int i = 0 ; i < depth ; i ++) {
res.append("--");
}
return res.toString();
}
public static void main(String[] args) {
BinarySearchTree<Integer> tree = new BinarySearchTree<>();
tree.add(6);
tree.add(8);
tree.add(4);
tree.add(2);
tree.add(11);
System.out.println(tree);
}
}
其他话题
二分搜索树的顺序性
因为二分搜索树的特性,二分搜索树中的元素其实都是有序的,我们使用深度优先算法中中序遍历的方式进行遍历,就能够自然地对树中的元素进行从小到大的排序。
那么由于有这种顺序性,我们就可以找到二分搜索树中的最大值和最小值,就比如我们上一节中实现的minimum()和maximum()方法。
甚至我们还能够根据这个特性,实现给定一个值,拿到它的前驱和后继successor()和predecessor()
根据这个特性,我们也能够实现floor(E e)和ceil(E e)方法即在二分搜索树中,找到比e小的最大的元素和比e大的最小元素。

和寻找前驱后继相似,但是这两个方法的元素,不一定需要再二分搜索树中。
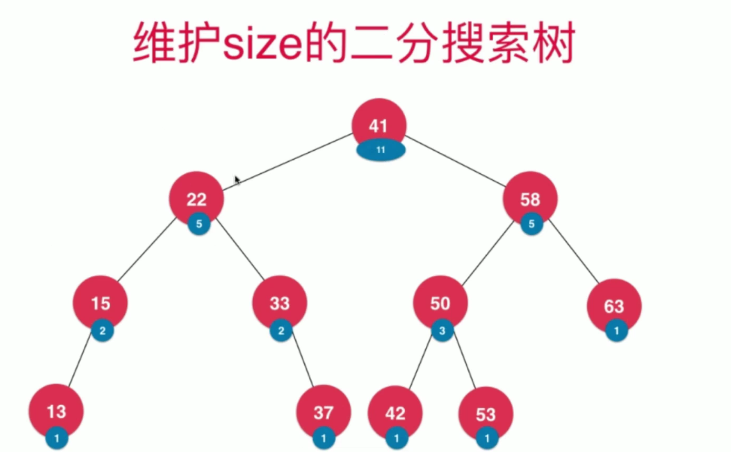
根据这个特性,我们也能够实现rank(E e)和select(int i)方法,即获得元素e在二分搜索树中的排名 和寻找排名为i的元素
为了实现这两个方法,有一个小技巧,就是使用维护size的二分搜索树,即在每个节点中,维护子树的节点数量
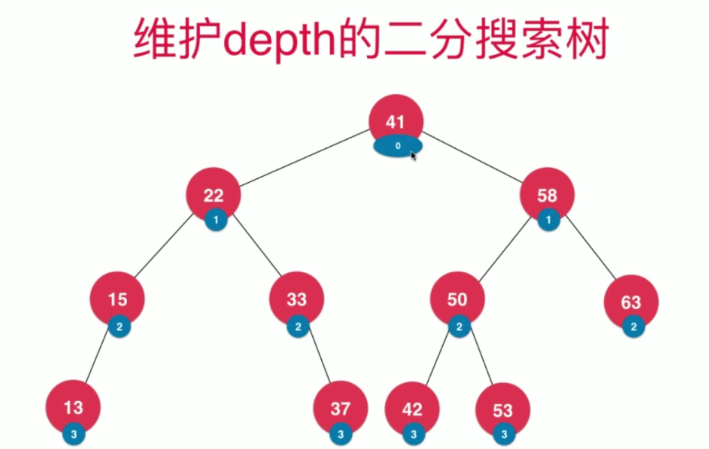
维护深度值
对于二分搜索树,也可以对每一个节点维护一个深度值
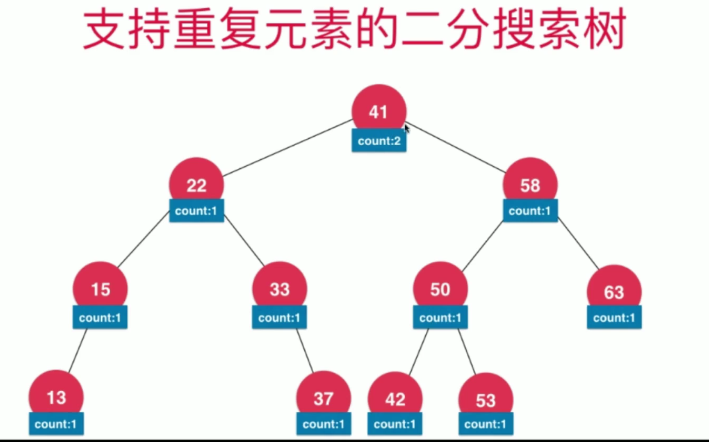
支持重复元素的二分搜索树
两种方案:
- 左子树都小于等于节点 ,右子树都大于节点
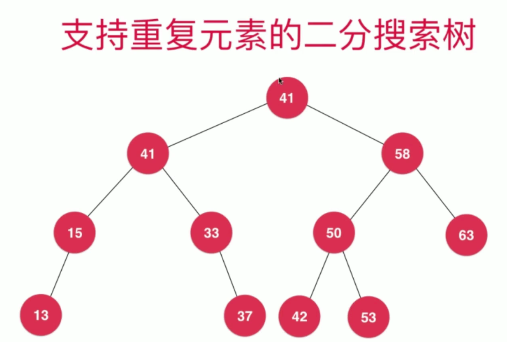
- 每一个节点维护一个count属性,记录当前节点有多少重复的元素