中心极限定理&&正态分布 随想
0-前言
笔者本来周末约好朋友出去骑行，不料天公不作美！哎，闲来无事来到了实验室，本来打算看看《天天向上》，而这一期又实在不好看（偶像剧）。只好来做做一些小实验，脑海里突然想到“正态分布“。于是乎我就开始琢磨用中心极限定理去简单验证一下”正态分布“。
1-工具
工具：当然是用的Python啦，嘿嘿。功能强大~
2-前期储备知识
1） 切尔雪夫不等式，
设随机变量X具有数学期望,方差则对任意正数ε，
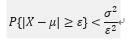
不等式成立。
意义： 切尔雪夫不等式说明，X的方差越小，事件发生的概率越大。即：X取的值基本上集中在期望附近。
2） 大数定理
设 ，....是一列相互独立的随机变量(或者两两不相关)，他们分别存在期望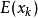
和方差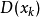
。若存在常数C使得：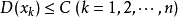
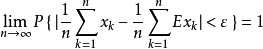
意义： 当n很大时，随机变量的平均值Yn在概率意义下无限接近期望。注意：出现偏离是可能的，但这种可能性很小，当n无限大时，这种可能性的概率为0.其中这里有一个误区就是： “概论为0就不发生”，事实上这时错误的。详情还请读者自行查阅。
3） 如何证明大数定理呢？
笔者也是自己证明啦，考虑到要花很长时间才能写出来，就不赘述啦，读者可自行查阅相关资料。在这里我只给出提示：根据Y的定义，求出它的期望和方差，代入切尔雪夫不等式即可！
4） 中心极限定理
当然这里只介绍“独立同分布”的中心极限定理啦，因为我要验证“正态分布”嘛~
设随机变量X1，X2，......Xn，......独立同分布，并且具有有限的数学期望和方差：E(Xi)=μ，D(Xi)=σ20(k=1,2....)，则对任意x，分布函数
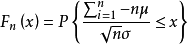
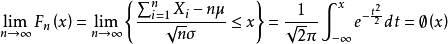
注意：该定理说明，当n很大时，随机变量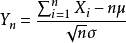
近似地服从标准正态分布N(0，1)。因此，当n很大时， 
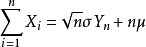近似地服从正态分布N(nμ，nσ2)
中心极限定理的意义： 实际问题中，很多随机现象可以看做许多因素的独立影响的综合反应，往往近似服从正态分布。
例如： 1.城市的耗电量呀 ：大量用户的耗电量的总和
2.测量误差呀 ： 许多观察不到的，微小误差的总和
注意：是多个随机变量的和才可以，有些问题是乘性误差，则需要鉴别或者取对数后使用，
3.线性回归中，将使用该定理论证最小二乘法的合理性！
3-Python 验证：
import numpy
import matplotlib.pyplot as plt
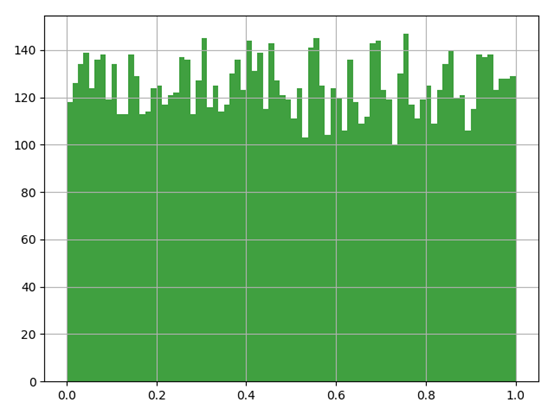
u = numpy.random.uniform(0.0,1.0,10000)
plt.hist(u,80,color='g',alpha = 0.75)
plt.grid(True)
plt.show()
times = 10000
for time in range(times):
u += numpy.random.uniform(0.0,1.0,10000)
print(len(u))
u/=times
print(len(u))
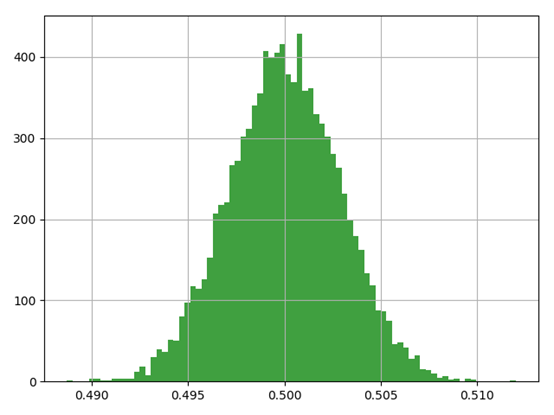
plt.hist(u,80,color='g',alpha = 0.75)
plt.grid(True)
plt.show()
