C++中的分治算法及常见题目汇总

目录

一、分治法基本原理

1. 分治算法基本介绍
2. 分治算法通俗解释

二、Leecode刷题题解

1. 最大子序和
2. 合并两个排序的链表
3. 数组中出现次数超过一般的数字
4. 最小的k个数(TopK问题)

 

 

一、分治法基本介绍

1. 分治算法基本介绍

　　分治算法即分而治之，就是把一个复杂的问题分解成两个或多个相同或相似的子问题，再把子问题分解成更小的问题。。。直到最后子问题可以简单地直接求解，原问题即子问题的合并。分治算法主要分为三个步骤：

• 分解：将问题划分成一系列子问题，子问题的形式和原问题一样，只是规模更小
• 解决：递归地求出子问题。如果子问题的规模足够小，即停止递归，直接求解
• 合并：步骤将子问题的解组合成原问题的解

2. 分治算法通俗解释

(此例子引用连接如下：https://www.zhihu.com/search?type=content&q=%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95)　　

　　有这样一个经典的问题：有100枚硬币，其中1枚重量与众不同，是假币，更轻一些。如果用天平秤，请问至少称多少次一定能找到这枚假币

　　加入我们用传统的枚举法，显然至少需要比较50次

      

 

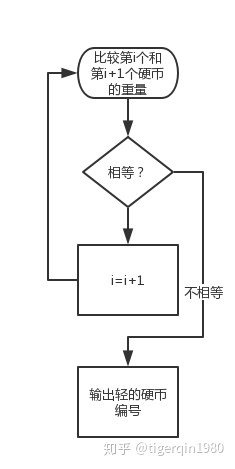
而假设我们采用分治法的话 ，流程如下：1. 将100硬币分成3份，33,33,34。

2.称量1、2份，若天平平衡，则假币必在另外34枚中。若不平衡，假币在轻的那33枚里。

3.将34枚分为11/11/12枚（或将33枚分成11*3）。

4.称量两组11枚的硬币，若平衡，假币在12枚里（或另外的11枚）若不平衡，假币在轻的11里。

5.将11（或12）枚分成3/4/4（或4/4/4），称量4/4，方法同上。

6.将剩下的3（或4）分为1/1/1（或1/1），称量1/1，若平衡，则剩下的一枚是假币，若不平衡，轻的是假币。 若还剩4枚，出现1/1平衡，剩下2枚则称量，显然轻的是假币。

这种方法只需要5次就能解决这个问题。

分治算法的流程：

 

 

二、Leecode刷题详解

1. 最大子序和

• 题目描述

　　

 

•  问题分析

　　解决此问题有两种方法：

• • 方法一：传统暴力解决方法，需要遍历整个数组，其时间复杂度为 O(n)

　　　　　设置一个当前最大值和全局最大值，遍历整个数组，当此时的最大值小于0时，则前面的都不要，否则，将下一个数相加即可　

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        /*
        要实现求得连续子数组的最大和,我们可以
        */
        if(array.empty())
            return 0;
        int cursum=0;
        int maxsum=array[0];
        for(int i=0;i<array.size();++i)
        {
            if(cursum<=0)
                cursum=array[i];
            else
            {
                cursum+=array[i];
            }
            if(cursum>=maxsum)
                maxsum=cursum;
        }
        return maxsum;
    }
};

• • 方法二：使用分治算法

　　　　要找到最大连续和的子数组，我们可以用分治算法，设最左边为left,最右边为right，中间节点为mid，则最大子数组可以分为以下三种情况：

　　　　1. 最大连续子数组都左边子数组[left, mid]

　　　　2. 最大连续子数组都在右边子数组[mid+1,right]

　　　　3. 最大连续子数组跨越了中点，一部分在左边子数组中，一部分在右边子数组中

　　　　最大连续子数组一定是三种情况中的最大值

class Solution {
    /*
        要找到连续最大子序和，我们可以用分治算法，设最左边为left, 最右边为right,中间节点为mid，则最大连续子数组可能情况为以下三种：
        1. 最大连续子数组都在[left, mid]中
        2. 最大连续子数组都在[mid+1, right]中
        3. 最大连续子数组跨越了中点，因此left<=i<=mid<=j<=right
    */
    //只需要在这三种情况中找出最大值即可
    //首先是求出mid在子数组中间的情况
    /*
        我们的目的是找出mid在子数组中的子数组的和
    */
    int INT_MIN=-2147483648; 
    public int find_max_cross_substr(int[] nums,int left,int mid,int right)
    {
        int maxleft=0,maxright=0;
        int sum=0;
        int leftsum=INT_MIN,rightsum=INT_MIN;
        //首先找到左半边子数组的最大值
        for(int i=mid;i>=left;--i)
        {
            sum+=nums[i];
            leftsum=Math.max(sum,leftsum);
        }
        //然后找到右半边子数组的最大值
        sum=0;
        for(int j=mid+1;j<=right;++j)
        {
            sum+=nums[j];
            rightsum=Math.max(sum,rightsum);
        }
        return (leftsum+rightsum);
    }
    //然后进行递归查找，比较三种情况，找出最大值
    public int find_max_substr(int[]nums,int left,int right)
    {
        if(left==right)
            return nums[left];//找到递归结束条件，结束递归
        else
        {
            int mid=left+(right-left)/2;
            int maxleftsum,maxrightsum,maxcrosssum;
            maxleftsum=find_max_substr(nums,left,mid);
            maxrightsum=find_max_substr(nums,mid+1,right);
            maxcrosssum=find_max_cross_substr(nums,left,mid,right);
            return Math.max(Math.max(maxleftsum,maxrightsum),maxcrosssum);
        }
        
    }
    public int maxSubArray(int[] nums) {
        return find_max_substr(nums,0,nums.length-1);
    }
}

class Solution {
    /*
        要找到连续最大子序和，我们可以用分治算法，设最左边为left, 最右边为right,中间节点为mid，则最大连续子数组可能情况为以下三种：
        1. 最大连续子数组都在[left, mid]中
        2. 最大连续子数组都在[mid+1, right]中
        3. 最大连续子数组跨越了中点，因此left<=i<=mid<=j<=right
    */
    //只需要在这三种情况中找出最大值即可
    //首先是求出mid在子数组中间的情况
    /*
        我们的目的是找出mid在子数组中的子数组的和
    */
    int INT_MIN=-2147483648; 
    public int find_max_cross_substr(int[] nums,int left,int mid,int right)
    {
        int maxleft=0,maxright=0;
        int sum=0;
        int leftsum=INT_MIN,rightsum=INT_MIN;
        //首先找到左半边子数组的最大值
        for(int i=mid;i>=left;--i)
        {
            sum+=nums[i];
            leftsum=Math.max(sum,leftsum);
        }
        //然后找到右半边子数组的最大值
        sum=0;
        for(int j=mid+1;j<=right;++j)
        {
            sum+=nums[j];
            rightsum=Math.max(sum,rightsum);
        }
        return (leftsum+rightsum);
    }
    //然后进行递归查找，比较三种情况，找出最大值
    public int find_max_substr(int[]nums,int left,int right)
    {
        if(left==right)
            return nums[left];//找到递归结束条件，结束递归
        else
        {
            int mid=left+(right-left)/2;
            int maxleftsum,maxrightsum,maxcrosssum;
            maxleftsum=find_max_substr(nums,left,mid);
            maxrightsum=find_max_substr(nums,mid+1,right);
            maxcrosssum=find_max_cross_substr(nums,left,mid,right);
            return Math.max(Math.max(maxleftsum,maxrightsum),maxcrosssum);
        }
        
    }
    public int maxSubArray(int[] nums) {
        return find_max_substr(nums,0,nums.length-1);
    }
}

 

 2. 合并两个排序的链表

• 题目描述

　　

 

•  问题分析

　　(1) 使用while循环。思路：将链表B合并到链表A中。循环链表B，需要创建两个指针，一个指向当前的节点，另一个指向当前的下一个结点。

　　(2) 分治算法+递归。思路：将两个链表中，l1指针和l2指针指向的节点，比较大小，然后递归即可，注意需要添加递归结束的代码

• 代码参考

　　

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode head=null;
        if(l1==null)
            return l2;
        else if(l2==null)
            return l1;
        else
        {
            if(l1.val<l2.val)
            {
                head=l1;
                head.next=mergeTwoLists(l1.next,l2);
            }
            else
            {
                head=l2;
                head.next=mergeTwoLists(l1,l2.next);
            }
        }
        return head;
    }
}

 

3. 数组中出现次数超过一半的数字

• 题目描述

　　

 

•  问题分析

　　数组中出现次数超过一半的数字特征如下：数字中出现次数超过一半的数字出现总次数大于其余数字出现次数的总数

　　首先我们可以设置一个出现次数times，初始值为0

　　若当前数组的数等于上一次出现的次数，则times++

　　否则，times--

• 代码参考

class Solution {
    public int majorityElement(int[] nums) {
        //如果一个数字出现的次数是数组长度的一半，则这个数组满足以下要求
        /*
            首先，这个数字出现的次数比其他数字出现的次数加起来还多
            我们可以设置一个出现次数times，初始化为0
            若当前数组的数等于上一个出现的次数，则times++
            否则times--
        */
        if(nums.length==0)
            return 0;
        int times=0;
        int result=nums[0];
        for(int i=0;i<nums.length;++i)
        {
            if(times==0)
                result=nums[i];
            if(result==nums[i])
                ++times;
            else
                --times;
        }
        int count=0;
        for(int i=0;i<nums.length;++i)
        {
            if(nums[i]==result)
                ++count;
        }
        if(count*2>nums.length)
            return result;
        else
            return 0;
    }
}

 

4. 最小的k个数(TopK问题)

• 题目描述

• 方法一(最大堆实现)

　　这是一道典型的TopK问题，比较直观的方法是利用堆数据结构来辅助得到最小的k个数。堆的性质是每次可以找出最大或者最小的元素。我们可以使用一个大小为k的最大堆(大堆顶)，将数组中的元素依次入堆，当堆的大小超过k时，便将多出的元素从堆顶弹出。如果数组中待插入的元素与堆顶元素进行比较，若待插入元素小于堆顶元素，则将堆顶元素弹出后将待插入元素插入堆

　　这样，由于每次从堆顶弹出的数都是堆中最大的，最小的k个元素一定会留在堆中。这样，把数组中的元素全部入堆后，堆中剩下的元素就是最大的k个数了。

• 代码参考

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        /*
            可以使用一个大根堆实时维护数组的前k个小值
            首先将k个数插入大根堆中
            然后从k+1个数开始遍历
                如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到额数
                最后将大根堆的数存入数组返回即可
        */
        if(k==0)
            return new int[0];
        //使用一个最大堆实现TopK问题
        //Java的priorityQueue默认是小堆顶，添加comparator参数使其变成大堆顶
        Queue<Integer> pq=new PriorityQueue<>(k,(i1,i2)->Integer.compare(i2,i1));

        //首先把数组中的前k个数字入堆
        for(int num:arr)
        {
            if(pq.size()<k)
                pq.offer(num);
            else if(num<pq.peek())
            {
                pq.poll();
                pq.offer(num);
            }
        }
        //返回堆中的元素
        int []res=new int[pq.size()];
        int idx=0;
        for(int num:pq)
        {
            res[idx++]=num;
        }
        return res;
    }
}

• 方法二：快速排序思想(分治算法)

　　可以使用快速排序思想来做，其是分治的思想

　　快速排序中有一步很重要的操作是partition(划分)，从数组中随机选取一个枢纽元素v，然后原地移动数组中的元素，使得v小的元素在v的左边，比v大的元素在v的右边，如下图所示：

　　

 

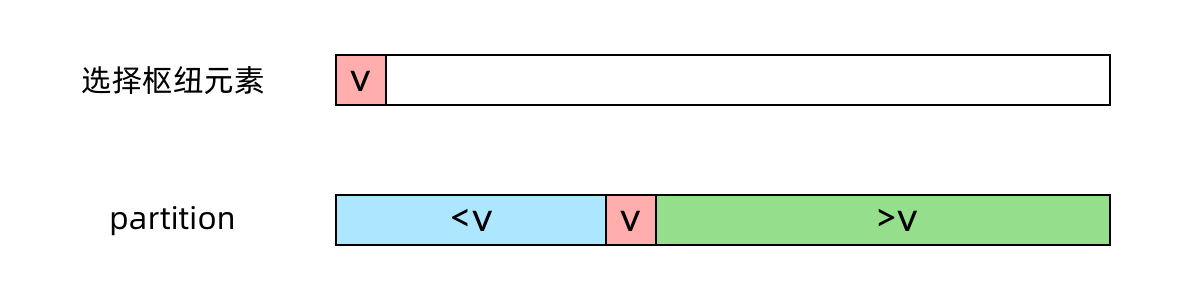
 　　我们的目的是寻找最小的k个数。假设经过一次partition操作，枢纽元素位于下标m，也就是说，左侧的数组有m个元素，是原数组中最小的m个数，那么：

• • 若k=m，我们就找到了最小的k个数，就是左侧的数组
  • 若k<m，则最小的k个数一定在左边数组，我们只需要对左侧数组递归即可
  • 若k>m，则左侧数组中的m个数都属于最小的k个数，我们还需要在右侧数组中寻找最小的k-m个数，对右侧数组递归地partition即可
• 代码参考

class Solution {
    /*
        方法二，可以利用快速排序的思想
        快速排序中有一个很重要的一步就是partition，从数组中随机选取一个元素v，然后原地移动数组中的元素，使得比v小的元素在v的左边，比v大的元素在v的右边
        我们的目的是找到最小的k个数，假设经过一次partition操作，枢纽元素位于下标m，
            若k==m，则找到最小的k个元素，即左侧的数组
            若k<m，则最小的k个数一定在左侧数组中，只需要对左侧数组中寻找最小的k-m个数即可
            若k>m，左侧数组中的m个数都属于最小的k个数，我们还需要右侧数组中寻找最小的k-m个数，对右侧数组递归的partition即可        
    */
    public int[] getLeastNumbers(int[] arr, int k) {
        if(k==0)
            return new int[0];
        else if(arr.length<=k)
            return arr;
        //原地不断划分数组
        partitionArray(arr,0,arr.length-1,k);
        //数组的前k个数此时就是最小的k个数，将其存入结果
        int[] res=new int[k];
        for(int i=0;i<k;++i)
        {
            res[i]=arr[i];
        }
        return res;

    }
    int partition(int[] arr,int low,int high)
    {
        int i=low;
        int j=high+1;
        int pivot=arr[low];
        while(true)
        {
            //左边：小而移动，大而赋值
            while(arr[++i]<pivot)
            {
                if(i==high)
                    break;
            }
            //右边：大而移动，小而赋值
            while(arr[--j]>pivot)
            {
                if(j==low)
                    break;
            }
            if(i>=j)
                break;
            swap(arr,i,j);
        }
        swap(arr,low,j);
        return j;
    }
    void swap(int[]arr,int i,int j)
    {
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }
    void partitionArray(int [] arr,int low,int high,int k)
    {
        //实现第一次partition
        int m=partition(arr,low,high);
        if(m==k)
            //刚好找到最小的k个数
            return;
        else if(k<m)
        {
            //最小的k个数一定在前m个数中，递归划分
            partitionArray(arr,low,m-1,k);
        }
        else
        {
            //在右侧数组中寻找最小的k-m个数
            partitionArray(arr,m+1,high,k);
        }
    }
}